|
Зачем необходимы треугольные нормы и конормы? Как их использовать? Имеется ввиду, на практике. |
Методы построения функции принадлежности. Обзор основных методов
Прямые методы для группы экспертов
При интерпретации степени принадлежности как вероятности было предложено
получать функции принадлежности для нескольких классов понятий 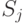 расчетным
путем, используя равенство
расчетным
путем, используя равенство 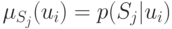 , где
условная вероятность определяется по формуле Байеса:
, где
условная вероятность определяется по формуле Байеса:
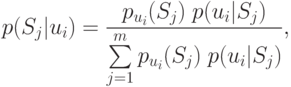
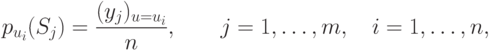
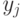 — число случаев при значении параметра
— число случаев при значении параметра  , когда верной
оказалась
, когда верной
оказалась  -я гипотеза.
-я гипотеза.Я.Я.Осис предложил следующую методику оценки функции принадлежности.
Первоначально определяется то максимальное количество классов, которое может
быть
описано данным набором параметров. Для каждого элемента  значение функции
принадлежности класса
значение функции
принадлежности класса  дополняет до единицы значения функции
принадлежности
класса
дополняет до единицы значения функции
принадлежности
класса 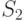 (в случае двух классов). Таким образом, система
должна состоять
из классов, представляющих противоположные события. Сумма значений функции
принадлежности произвольного элемента
(в случае двух классов). Таким образом, система
должна состоять
из классов, представляющих противоположные события. Сумма значений функции
принадлежности произвольного элемента  к системе таких классов
будет равна
единице. Если число классов и их состав четко не определены, то необходимо
вводить
условный класс, включающий те классы, которые не выявлены. Далее эксперты
оценивают в процентах при данном состоянии
к системе таких классов
будет равна
единице. Если число классов и их состав четко не определены, то необходимо
вводить
условный класс, включающий те классы, которые не выявлены. Далее эксперты
оценивают в процентах при данном состоянии  степень проявления
каждого класса
из названного перечня.
степень проявления
каждого класса
из названного перечня.
Однако в некоторых случаях мнение эксперта очень трудно выразить в
процентах,
поэтому более приемлемым способом оценки функции принадлежности будет метод
опроса, который состоит в следующем. Оцениваемое состояние предъявляется
большому
числу экспертов, и каждый имеет один голос. Он должен однозначно отдать
предпочтение одному из классов заранее известного перечня. Значение функции
принадлежности вычисляется по формуле  ,
где
,
где  — число экспертов, участвовавших в эксперименте, и
— число экспертов, участвовавших в эксперименте, и 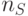 —
число экспертов, проголосовавших за класс
—
число экспертов, проголосовавших за класс  .
.
Пример.
Пусть в результате переписи населения в некоторой области с численностью
жителей  получено множество значений возраста
получено множество значений возраста ![U=[0,100]](/sites/default/files/tex_cache/377f2169410ceebd7a593690a9e6f9e0.png) . Пусть
. Пусть 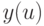 —
число людей, имеющих возраст
—
число людей, имеющих возраст  и утверждающих, что являются
молодыми.
Пусть
и утверждающих, что являются
молодыми.
Пусть  — действительное число людей, имеющих возраст
— действительное число людей, имеющих возраст  ;
тогда
;
тогда 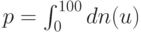 . Можно считать, что
понятие "МОЛОДОЙ" описывается нечетким множеством на
. Можно считать, что
понятие "МОЛОДОЙ" описывается нечетким множеством на  с функцией
принадлежности
с функцией
принадлежности 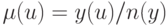 . Очевидно, что для малых
значений возраста
. Очевидно, что для малых
значений возраста  , следовательно,
, следовательно, 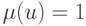 . Однако, не
все
. Однако, не
все 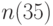 считают себя молодыми, следовательно,
считают себя молодыми, следовательно,  . Для
. Для  число
число 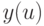 должно быть очень маленьким.
должно быть очень маленьким.
