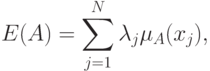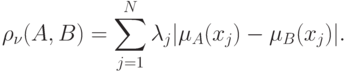|
Зачем необходимы треугольные нормы и конормы? Как их использовать? Имеется ввиду, на практике. |
Лекция 4: Показатель размытости нечетких множеств. Нечеткие меры и интегралы
Метрический подход к определению показателя размытости нечетких множеств
Показатель размытости нечетких множеств можно
определить с помощью
метрики как меру отличия нечеткого множества от ближайшего к нему обычного
множества. Другой способ задания показателя размытости с помощью метрики
—
это определение его с помощью расстояния до максимального размытого
множества 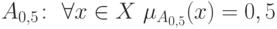 и расстояния
между нечетким множеством и его дополнением. Оказывается, эти подходы имеют
много общего между собой, и определяемый с помощью метрики показатель размытости
обладает многими свойствами, сформулированными выше.
и расстояния
между нечетким множеством и его дополнением. Оказывается, эти подходы имеют
много общего между собой, и определяемый с помощью метрики показатель размытости
обладает многими свойствами, сформулированными выше.
Множеством, ближайшим к нечеткому множеству  , называется
неразмытое множество
, называется
неразмытое множество 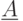 такое, что
такое, что
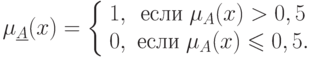
Показателем размытости называется функционал
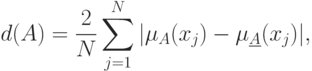
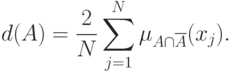
Если вместо расстояния Хэмминга использовать евклидово расстояние, то получим

Показатель размытости можно задать с помощью расстояния между нечетким множеством и его дополнением:
![d(A) = k\left[ {\rho (\varnothing ,U) - \rho (A,\bar A)}
\right]
.](/sites/default/files/tex_cache/2044a87127b80c5ff0996c367daff98a.png)
В случае метрики Хэмминга 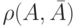 имеет вид
имеет вид
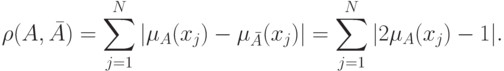
Такой показатель размытости удовлетворяет свойствам Р1 и Р2.
Далее выясним, что между показателями размытости, удовлетворяющими условиям Р1, Р2, Р3, и метриками определенного класса может быть установлено взаимно однозначное соответствие.
Связь показателя размытости с алгебраическими свойствами решетки нечетких множеств
Существование показателя размытости нечетких множеств оказывается тесно связанным со свойствами алгебры нечетких множеств Заде. Для алгебры обычных множеств показатель размытости со свойствами Р1, Р2, Р3 вырождается в тривиальный показатель, всюду равный нулю. Для более общих алгебр такого показателя просто не существует. Укажем соотношения, существующие между произвольными положительными оценками и показателями размытости.
Положительной оценкой на решетке нечетких множеств 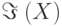 называется функция
называется функция 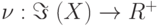 , удовлетворяющая свойству
, удовлетворяющая свойству

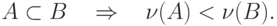
Положительная оценка  определяет на
определяет на 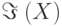 метрику
метрику
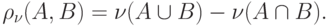
Решетка 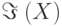 с положительной оценкой
с положительной оценкой  и метрикой
и метрикой 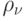 называется метрической решеткой нечетких множеств. Метрика
называется симметричной, если она удовлетворяет условию
называется метрической решеткой нечетких множеств. Метрика
называется симметричной, если она удовлетворяет условию

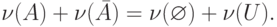
Теорема. В метрической решетке нечетких множеств функционалы
![\begin{gathered}
d(A) = 2k\left[ {\nu (U) - \nu (A \cup \bar A)} \right], \hfill \\
d(A) = 2k\left[ {\nu (A \cap \bar A) - \nu (\varnothing )} \right], \hfill \\
d(A) = k\left[ {\rho _\nu (\varnothing ,U) - \rho _\nu (A,\bar A)} \right]
\hfill \\
\end{gathered}](/sites/default/files/tex_cache/1afc8f941772ac97cb008c8cf3bd9063.png)
 ,
,  ,
,  . Они попарно тождественны
тогда и только тогда, если положительная оценка
. Они попарно тождественны
тогда и только тогда, если положительная оценка  симметрична.
симметрична.Примером симметричной оценки на решетке нечетких множеств может служить энергия нечеткого множества: