Быстрая сортировка

Размер стека

Так же как и в "Элементарные структуры данных" , для быстрой сортировки можно применить явный стек магазинного типа, используя его для хранения информации о еще не обработанных подфайлах, которые ожидают сортировки. Каждый раз, когда нужно обработать подфайл, он выталкивается из стека. При разбиении файла получаются два не обработанных подфайла, и они помещаются в стек. В рекурсивной реализации, представленной программой 7.1, эту информацию содержит стек, поддерживаемый системой.

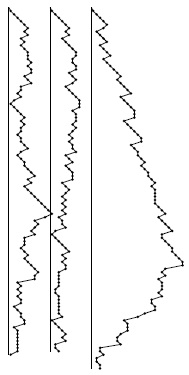
Для случайно упорядоченных файлов максимальный раздел стека пропорционален log N (см. раздел ссылок), но в вырожденных случаях стек может вырасти до размера, пропорционального N, что показано на рис. 7.5. Ведь наихудший случай - это когда входной файл уже отсортирован. Потенциальная возможность роста стека до размера, пропорционального размеру входного файла представляет собой не очевидную, но вполне реальную проблему для рекурсивной реализации быстрой сортировки: стек, пусть и неявно, используется всегда, а вырожденный файл большого размера может стать причиной аварийного завершения программы из-за нехватки памяти. Конечно, для библиотечной программы сортировки такое поведение недопустимо. (На самом деле программе скорее не хватит времени, чем памяти.)

Рис. 7.5. Размер стека при работе быстрой сортировки

Рекурсивный стек для быстрой сортировки не бывает большим при обработке случайно упорядоченных файлов, но в вырожденных случаях он может занимать очень большой объем памяти. Здесь приведены графики размеров стека для двух случайно упорядоченных файлов (слева и в центре) и для частично упорядоченного файла (справа).

Трудно гарантированно исключить такое поведение программы, но в разделе 7.5 мы увидим, что несложно предусмотреть специальные средства, которые сведут вероятность возникновения таких вырожденных случаев почти к нулю.

Программа 7.3 представляет собой нерекурсивную реализацию, которая решает эту проблему, проверяя размеры обоих подфайлов и первым помещая в стек больший из них. На рис. 7.6 показана эта стратегия. Сравнивая данный пример с приведенным на рис. 7.1, мы видим, что это правило не изменяет подфайлы, меняется лишь порядок их обработки. Так что мы экономим память без изменения времени выполнения.

Программа 7.3. Нерекурсивная быстрая сортировка

Данная нерекурсивная реализация (см. "Рекурсия и деревья" ) быстрой сортировки использует явный стек магазинного типа, заменяя рекурсивные вызовы помещением в стек параметров, а рекурсивные вызовы процедур и выходы из них - циклом, выталкивающим параметры из стека и обрабатывающим их, пока стек не пуст. Больший из двух подфайлов помещается в стек первым, чтобы максимальная глубина стека при сортировке N элементов не превосходила lgN (см. свойство 7.3).

  #include "STACK.cxx"
  inline void push2(STACK<int> &s, int A, int B)
    { s.push(B); s.push(A); }
template <class Item>
  void quicksort(Item a[], int l, int r)
    { STACK<int> s(50)); push2(s, l, r);
      while (!s.empty())
        {
l = s.pop(); r = s.pop();
if (r <= l) continue;
int i = partition(a, l, r);
if (i-1 > r-i)
  { push2(s, l, i-1); push2(s, i+1, r); }
else
  { push2(s, i+1, r); push2(s, l, i-1); }
        }
    }
        

Рис. 7.6. Пример работы быстрой сортировки (вначале упорядочивается меньший подфайл)

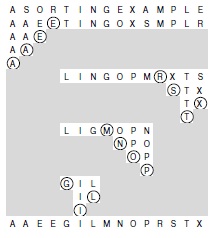
Порядок обработки подфайлов не влияет ни на корректность работы алгоритма быстрой сортировки, ни на время выполнения, однако он может повлиять на размер стека, необходимого для поддержки рекурсивной структуры. Здесь после каждого разбиения вначале обрабатывается меньший из двух подфайлов.

Правило, согласно которому больший из двух подфайлов помещается в стек первым, обеспечивает, что каждый элемент стека имеет размер, не больший половины элемента под ним, так что стеку нужна память только для порядка lgN элементов. Это максимальное заполнение стека имеет место, если разбиение всегда попадает в центр файла. Для случайно упорядоченных файлов реальный максимальный размер стека гораздо меньше; для вырожденных файлов он обычно мал.

Рис. 7.7. Дерево разбиений быстрой сортировки

Если свернуть диаграммы разбиений на рис. 7.1 и рис. 7.6, соединив каждый центральный элемент с центральными элементами из двух его подфайлов, то получится такое статическое представление процесса разбиения (в обоих случаях). В данном бинарном дереве каждый подфайл представлен своим центральным элементом (или целиком подфайлом, если его размер равен 1), а поддеревья каждого узла представляют подфайлы после их разбиения. Чтобы не загромождать рисунок, пустые подфайлы здесь не показаны, хотя наши рекурсивные версии алгоритма выполняют рекурсивные вызовы при r < l, т.е. когда центральный элемент является наименьшим или наибольшим в файле. Вид дерева не зависит от порядка разбиения подфайлов. Наша рекурсивная реализация быстрой сортировки соответствует посещению узлов дерева в прямом порядке, а нерекурсивная реализация соответствует правилу посещения вначале меньшего поддерева.

Этот метод не обязательно будет работать в настоящей рекурсивной реализации, поскольку он зависит от освобождения стека перед выходом или после выхода (end-или tail-recursion removal). Если последним действием какой-либо процедуры является вызов другой процедуры, то некоторые системы программирования удаляют локальные переменные из стека до вызова, а не после. Без освобождения стека перед выходом невозможно гарантировать, что размер стека, используемого быстрой сортировкой, будет мал. Например, вызов быстрой сортировки для уже отсортированного файла размером N породит рекурсивный вызов для такого же файла, но размером N - 1, который, в свою очередь, породит рекурсивный вызов для файла размером N - 2 и т.д., и наконец нарастит глубину стека пропорционально N. Это наблюдение подталкивает к использованию нерекурсивной реализации, не допускающей чрезмерный рост стека. C другой стороны, некоторые компиляторы C++ автоматически вставляют освобождение стека перед выходом, и многие машины имеют аппаратную поддержку вызовов функций - поэтому в таких средах нерекурсивная реализация из программы 7.3 может оказаться более медленной, чем рекурсивная реализация из программы 7.1.

На рис. 7.7 еще раз проиллюстрирован тот факт, что для любого файла нерекурсивный метод обрабатывает те же подфайлы (но в другом порядке), что и рекурсивный метод. На нем показана древовидная структура с центральным элементом в корне и его левым и правым поддеревьями, соответствующими левому и правому подфайлам. Использование рекурсивной реализации быстрой сортировки соответствует обходу этих узлов в прямом порядке; нерекурсивная реализация соответствует правилу просмотра сначала наименьшего поддерева.

При явном использовании стека, как в программе 7.3, удается избежать некоторых затрат, присущих рекурсивной реализации, хотя современные системы программирования обеспечивают минимум затрат для таких простых программ. Программа 7.3 может быть еще улучшена. Например, она помещает в стек оба подфайла только для того, чтобы тут же вытолкнуть верхний из них; можно улучшить ее, присваивая значения переменным l и r напрямую. Далее, проверка 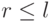выполняется после выталкивания подфайлов из стека, тогда как эффективнее вообще не помещать такие файлы в стек (см. упражнение 7.14). Может показаться, что это не важно, однако рекурсивный характер быстрой сортировки на самом деле приводит к тому, что значительная часть подфайлов в процессе сортировки имеет размеры 0 или 1. Ниже мы рассмотрим важное усовершенствование быстрой сортировки, которое использует эту идею - обрабатывать все подфайлы небольшого размера максимально экономично - для увеличения ее эффективности.

Упражнения

7.11. В стиле рис. 5.5 приведите содержимое стека после каждой пары операций поместить в стек и вытолкнуть из стека, если программа 7.3 используется для сортировки файла с ключами E A S Y Q U E S T I O N.

7.12. Выполните упражнение 7.11 для случая, когда в стек всегда сначала помещается правый подфайл, а затем левый подфайл (как это принято в рекурсивной реализации).

7.13. Завершите доказательство по индукции леммы 7.3.

7.14. Внесите в программу 7.3 такие изменения, чтобы она никогда не помещала в стек подфайлы с .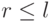

7.15. Приведите максимальный размер стека, требуемый программой 7.3 при N = 2ⁿ .

7.16. Приведите максимальные размеры стека, требуемые программой 7.3 при N = 2ⁿ - 1 и N = 2ⁿ + 1 .

7.17. Стоит ли для нерекурсивной реализации быстрой сортировки использовать вместо стека очередь? Обоснуйте ваш ответ.

7.18. Определите, выполняется ли в вашей системе программирования освобождение стека перед выходом.

7.19. Определите эмпирическим путем средний размер стека, используемого базовым рекурсивным алгоритмом быстрой сортировки для случайно упорядоченных файлов из N элементов, для N = 10³, 10⁴, 10⁵ и 10⁶ .

7.20. Определите среднее количество подфайлов размера 0, 1 и 2, если быстрая сортировка используется для сортировки случайно упорядоченного файла из N элементов.