Сбалансированные деревья

Описанные в предыдущей главе алгоритмы, в которых используются деревья бинарного поиска (BST-алгоритмы), успешно работают для широкого множества приложений, однако в худших случаях их производительность существенно снижается. Более того, как это ни прискорбно, худший случай стандартного BST-алгоритма, как и для быстрой сортировки, встречается чаще всего тогда, когда пользователь не следит за этим. Уже упорядоченные файлы, файлы с большим количеством повторяющихся ключей, обратно упорядоченные файлы, файлы с чередующимися большими и малыми ключами или файлы с любым большим сегментом данных простой структуры могут привести к квадратичному времени построения BST-дерева и линейному время поиска.

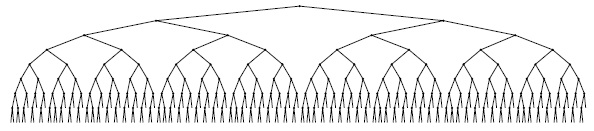
В идеальном случае можно было бы постоянно держать деревья полностью сбалансированными, подобно дереву, показанному на рис. 13.1. Эта структура соответствует бинарному поиску и, следовательно, гарантирует, что любой поиск может быть выполнен за менее чем lgN+1 сравнений, но в этом случае поддержка динамических вставок и удалений сопряжена с большими затратами. Высокая производительность поиска гарантирована для любого BST-дерева, в котором все внешние узлы расположены на одном или, в крайнем случае, на двух нижних уровнях. Существует множество таких BST-деревьев, поэтому в поддержке сбалансированности дерева имеется некоторая свобода. Если нас устраивают и деревья, близкие к оптимальным, эта свобода еще больше увеличивается.

Рис. 13.1. Большое полностью сбалансированное BST-дерево

Все внешние узлы этого BST-дерева находятся на одном из двух уровней, и для выполнения любого поиска требуется столько же сравнений, как и для поиска этого же ключа методом бинарного поиска (если бы элементы хранились в упорядоченном массиве). Наша цель — сохранение BST-дерева максимально сбалансированным при сохранении эффективности вставки, удаления и других операций с АТД словаря.

Например, существует очень много BST-деревьев, высота которых меньше 2lgN . Если можно смягчить стандарт, но при этом гарантировать, что алгоритмы будут строить только такие BST-деревья, то можно избежать снижения производительности для худших случаев, которые могут встретиться в реальных приложениях, работающих с динамическими структурами данных. При этом производительность в среднем также увеличивается.

Один из подходов к повышению сбалансированности BST-деревьев — их регулярная явная балансировка. Действительно, используя рекурсивный метод, показанный в программе 13.1, большинство BST-деревьев можно полностью сбалансировать за линейное время (см. упражнение 13.4). Скорее всего, такая балансировка повысит производительность для случайных ключей, но она не гарантирует исключения квадратичного времени выполнения операций в динамической таблице имен для худшего случая. С одной стороны, между операциями балансировки время вставки для последовательности ключей может квадратично зависеть от длины этой последовательности; с другой стороны, явную балансировку крупных деревьев нежелательно выполнять слишком часто, поскольку для выполнения каждой такой операции требуется время, по меньшей мере, линейно зависящее от размера дерева. Это взаимосвязь затрудняет использование глобальной балансировки для гарантирования высокой производительности в динамических BST-деревьях. Во всех рассматриваемых далее алгоритмах при обходе дерева выполняются локальные операции улучшения структуры, которые совместно увеличивают сбалансированность всего дерева, но при этом, в отличие от программы 13.1, не обходят все узлы.

Задача обеспечения гарантированной производительности для реализаций таблиц символов, основанных на использовании BST-деревьев — превосходный повод для исследования, а что же именно подразумевается под гарантированной производительностью. Мы рассмотрим решения этой задачи, являющиеся типичными примерами трех базовых подходов к обеспечению гарантированной производительности при разработке алгоритмов: рандомизации, амортизации и оптимизации. Сейчас мы кратко ознакомимся с каждым из этих подходов по очереди.

При использовании рандомизации принятие случайного решения выполняется в самом алгоритме, что радикально уменьшает вероятность возникновения худшего случая (независимо от входных данных). Мы уже видели применение такого подхода, когда в алгоритме быстрой сортировки в качестве центрального использовался случайный элемент. В разделах 13.1 и 13.5 мы рассмотрим рандомизированные BST-деревья и слоеные списки — два простых способа использования рандомизации в таблицах символов для увеличения эффективности реализаций всех операций АТД таблицы символов.

Программа 13.1. Балансировка BST-дерева

Используя функцию разбиения partR из программы 12.15, данная рекурсивная функция полностью балансирует BST-дерево за линейное время. Разбиение помещает средний узел в корень, а затем (рекурсивно) выполняет то же самое в поддеревьях.

  void balanceR(link& h)
    { if ((h == 0) || (h->N == 1)) return;
      partR(h, h->N/2);
      balanceR(h->l);
      balanceR(h->r);
    }
    

Эти алгоритмы просты и широко используются, однако они были открыты лишь недавно (см. раздел ссылок). Аналитическое доказательство эффективности этих алгоритмов довольно сложно, но сами алгоритмы просты для понимания, как и их реализация и практическое применение.

Амортизационный подход заключается в однократном выполнении дополнительных действий во избежание выполнения большего объема работы впоследствии, чтобы обеспечить гарантированный верхний предел средних затрат на одну операцию (общих затрат на все операции, разделенных на количество операций). В разделе 13.2 рассматривается скошенное дерево — вариант BST-дерева, который можно использовать для обеспечения такой гарантии в реализациях таблиц символов. Разработка этого метода послужила одним из стимулов разработки концепции амортизации (см. раздел ссылок). Этот алгоритм является очевидным расширением метода вставки в корень, рассмотренного в "Таблицы символов и деревья бинарного поиска" , но аналитическое обоснование предельных значений его производительности довольно сложно.

Оптимизационный подход обеспечивает гарантированную производительность каждой операции. На основе этого подхода были разработаны различные методы, часть из них — еще в 60-е годы. Эти методы требуют хранения в деревьях некоторой структурной информации, и, как правило, их реализация достаточно трудоемка. В этой главе будут рассмотрены две простые абстракции, которые не только делают реализацию понятной, но и обеспечивают почти оптимальные верхние пределы затрат.

После изучения реализаций АТД таблиц символов с использованием каждого из этих трех подходов, обеспечивающих гарантированно высокую производительность, в конце главы приведено сравнение характеристик производительности. Помимо различий, обусловленных различными принципами обеспечения производительности тем или иным алгоритмом, каждый из методов характеризуется необходимыми для этого (сравнительно небольшими) затратами времени или памяти. Разработка АТД действительно оптимально сбалансированного дерева все еще остается предметом исследований. Тем не менее, все рассматриваемые в этой главе алгоритмы весьма важны и способны обеспечить быстрые реализации операций найти и вставить (и ряда других операций АТД таблицы символов) в динамических таблицах символов, предназначенных для разнообразных приложений.

Упражнения

13.1. Реализуйте эффективную функцию, выполняющую балансировку BST-деревьев, не содержащих поле счетчика в своих узлах.

13.2. Измените стандартную функцию вставки в BST-дерево, приведенную в программе 12.8, чтобы ее можно было использовать в программе 13.1 для выполнения балансировки дерева каждый раз, когда количество элементов в таблице символов достигает числа, равного степени 2. Сравните время выполнения этой программы с временем выполнения программы 12.8 при выполнении задач (1) построения дерева из N случайных ключей и (2) поиска N случайных ключей в полученном дереве, для N = 10³, 10⁴, 10⁵ и 10⁶ .

13.3. Оцените количество сравнений, используемых программой из упражнения 13.2 при вставке возрастающей последовательности N ключей в таблицу символов.

13.4. Покажите, что для вырожденного дерева время выполнения программы 13.1 пропорционально NlgN. Затем приведите самый слабый вариант условия, накладываемого на структуру дерева, при котором время выполнения программы будет линейным.

13.5. Измените стандартную функцию вставки в BST-дерево, приведенную в программе 12.8, чтобы в ней выполнялось разбиение по медиане для любого узла, который в одном из своих поддеревьев содержит менее четверти своих узлов. Сравните время выполнения этой программы с временем выполнения программы 12.8 при выполнении задач (1) построения дерева из N случайных ключей и (2) поиска N случайных ключей в полученном дереве, для N = 10³, 10⁴, 10⁵ и 10⁶ .

13.6. Оцените количество сравнений, используемых программой из упражнения 13.5 при вставке в таблицу символов возрастающей последовательности N ключей.

13.7. Расширьте реализацию из упражнения 13.5, чтобы она выполняла балансировку и при выполнении операции удалить. Экспериментально определите, возрастает ли высота дерева при выполнении длиной последовательности чередующихся случайных вставок и удалений в случайном дереве из N узлов при N = 10, 100 и 1000 и для N² пар вставок-удалений для каждого N.