|
Здравствуйте прошла курсы на тему Алгоритмы С++. Но не пришел сертификат и не доступен.Где и как можно его скаачат? |
Сбалансированные деревья
Рандомизированные BST-деревья
Чтобы проанализировать средние затраты при работе с BST-деревьями, было сделано предположение, что элементы вставляются в случайном порядке (см. "Таблицы символов и деревья бинарного поиска" ). Применительно к BST-алгоритму основное следствие из этого предположения заключается в том, что каждый узел дерева с равной вероятностью может оказаться корневым, причем это же справедливо и по отношению к поддеревьям. Интересно, что случайность можно включить в алгоритм, чтобы это свойство сохранялось без каких-либо допущений относительно порядка вставки элементов. Идея проста: при вставке нового узла в дерево из N узлов вероятность появления нового узла в корне должна быть равна 1/(N + 1), поэтому нужно просто принять случайное решение использовать вставку в корень с этой вероятностью. Иначе рекурсивно выполняется вставка новой записи в левое поддерево, если ключ записи меньше ключа в корне, и в правое поддерево, если он больше. Реализация этого метода приведена в программе 13.2.
Программа 13.2. Вставка в рандомизированное BST-дерево
Эта функция принимает случайное решение о том, использовать ли метод вставки в корень из программы 12.13 или стандартный метод вставки из программы 12.8. В рандомизированном BST-дереве каждый из узлов с равной вероятностью может быть корнем; поэтому, помещая новый узел в корень дерева размером N с вероятностью 1/(N + 1), мы получаем рандомизированное дерево.
private:
void insertR(link& h, Item x)
{ if (h == 0) { h = new node(x); return; }
if (rand() < RAND_MAX/(h->N+1))
{ insertT(h, x); return; }
if (x.key() < h->item.key())
insertR(h->l, x);
else
insertR(h->r, x);
h->N++;
}
public:
void insert(Item x)
{ insertR(head, x); }
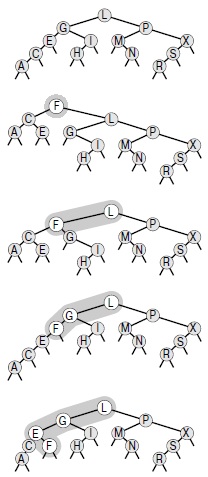
С нерекурсивной точки зрения выполнение рандомизированной вставки эквивалентно выполнению стандартного поиска вставляемого ключа с принятием на каждом шаге случайного решения о том, продолжить ли поиск или прервать его и выполнить вставку в корень. Таким образом, как показано на рис. 13.2, новый узел может быть вставлен в любое место на пути поиска. Это простое вероятностное объединение стандартного BST-алгоритма с методом вставки в корень обеспечивает гарантированную производительность в вероятностном смысле.
Лемма 13.1. Построение рандомизированного BST-дерева эквивалентно построению стандартного BST-дерева из случайной перестановки исходных ключей. Для создания рандомизированного BST-дерева из N элементов используется около 2NlnN сравнений (независимо от порядка вставки элементов), а для поиска в таком дереве требуется приблизительно 2 lnN сравнений.
Каждый элемент с равной вероятностью может быть корнем дерева, и это справедливо для обоих поддеревьев. Первая часть этого утверждения верна по построению, но для подтверждения того, что метод вставки в корень сохраняет случайность поддеревьев, требуется тщательное вероятностное обоснование (см. раздел ссылок). 
Новая запись в рандомизированном BST-дереве может располагаться в любом месте пути поиска записи, в зависимости от рандомизированных решений, принятых во время поиска. На этом рисунке показаны все возможные местоположения записи, содержащей ключ F, при ее вставке в дерево, показанное вверху.
Различие между производительностью в среднем для рандомизированных и стандартных BST-деревьев очень невелико, но имеет большое значение. Усредненные затраты в обоих случаях одинаковы (хотя для рандомизированных деревьев коэффициент пропорциональности несколько выше), однако в случае стандартных деревьев результат зависит от предположения о вставке элементов в случайном порядке их ключей (все последовательности вставок равновероятны). Во многих практических приложениях это допущение неверно, поэтому рандомизированный алгоритм важен тем, что позволяет избавиться от такого предположения и вместо этого опираться на законы теории вероятностей и степень случайности генератора случайных чисел. При вставке элементов в порядке возрастания их ключей, в обратном порядке или любом другом порядке — BST-дерево все равно будет случайным.
На рис. 13.3 рис. 13.3 показано построение рандомизированного дерева для некоторого набора ключей. Поскольку решения, принимаемые алгоритмом, являются случайными, то, скорее всего, последовательность деревьев при каждом выполнении алгоритма будет иной. На рис. 13.4 показано, что рандомизированное дерево, построенное из набора элементов, упорядоченных по возрастанию ключей, обладает теми же свойствами, что и стандартное BST-дерево, построенное из случайно упорядоченных элементов (сравните с рис. 12.8 рис. 12.8).
Существует вероятность, что при каждой возможности генератор случайных чисел будет приводить к неверному решению и в итоге к получению плохо сбалансированных деревьев, однако эту вероятность можно оценить математически и доказать, что она исчезающе мала.
Лемма 13.2. Вероятность того, что затраты на создание рандомизированного BST-дерева превышают усредненные затраты в а раз, меньше 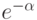 .
.
Этот результат и аналогичные ему следуют из общего решения вероятностных рекуррентных соотношений, которые были выведены Карпом (Karp) в 1995 г. (см. раздел ссылок). 
Например, для построения рандомизированного BST-дерева из 100 000 узлов требуется около 2,3 миллиона сравнений, но вероятность того, что количество сравнений превысит 23 миллиона, значительно меньше 0,01%. Подобная гарантия производительности более чем удовлетворяет практическим требованиям, предъявляемым к обработке реальных наборов данных такого размера. При использовании стандартного BST-дерева такая гарантия для этой задачи невозможна: например, производительность снизится, если данные в значительной степени упорядочены, что маловероятно для случайных данных, но по множеству причин достаточно часто бывает с реальными данными.
По тем же соображениям утверждение, аналогичное лемме 13.2, справедливо и для времени выполнения быстрой сортировки. Но в данном случае это более важно, поскольку отсюда следует еще и то, что затраты на поиск в дереве близки к средним. Независимо от дополнительных затрат при построении деревьев, стандартную реализацию BST-дерева можно использовать для выполнения операций найти при затратах, которые зависят только от формы деревьев, и при отсутствии каких-либо дополнительных затрат на балансировку. Это свойство важно в обычных приложениях, в которых операции найти встречаются гораздо чаще, чем любые другие. Например, описанное в предыдущем абзаце BST-дерево из 100 000 узлов могло бы содержать телефонный справочник и использоваться для выполнения миллионов поисков. Можно быть почти уверенным, что каждый поиск потребует затрат, которые отличаются от среднего значения, равного приблизительно 23 сравнениям, лишь небольшим постоянным коэффициентом. Поэтому на практике можно не беспокоиться, что для большого количества поисков потребуется порядка 100 000 сравнений, в то время как при использовании стандартных BST-деревьев для беспокойства были бы основания.
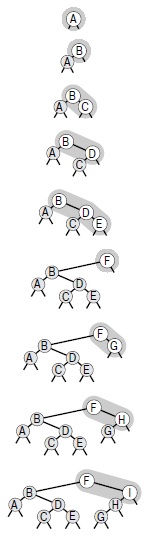
Один из главных недостатков рандомизированных вставок — затраты на генерацию случайных чисел в каждом из узлов во время каждой вставки.
На этих рисунках показан процесс рандомизированных вставок ключей A B C D E F G H I в первоначально пустое BST-дерево. Дерево на нижнем рисунке выглядит так же, как если бы оно было построено с применением стандартного алгоритма BST-дерева при вставке этих же ключей в случайном порядке.
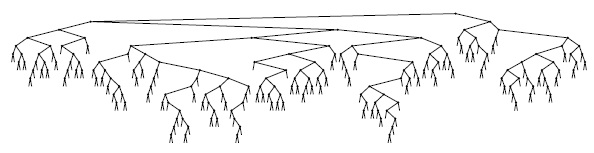
Это BST-дерево является результатом рандомизированных вставок 200 элементов в порядке возрастания их ключей в первоначально пустое дерево. Дерево выглядит так, как если бы оно было построено из случайно упорядоченных ключей (см. рис. 12.8).
Качественный системный генератор случайных чисел может работать с большой нагрузкой для генерации псевдослучайных чисел, обладающих большей степенью случайности, чем требуется для BST-деревьев. Поэтому в некоторых реальных ситуациях (например, если предположение о случайном порядке элементов справедливо) построение рандомизированного BST-дерева может оказаться более медленным, чем построение стандартного BST-дерева. Как и в случае быстрой сортировки, эти затраты можно снизить, используя числа, которые являются не совсем случайными, но не требуют больших затрат на их генерацию и достаточно подобны случайным числам, чтобы исключить возникновение худших случаев для BST-деревьев при таких последовательностях вставок ключей, которые обычно встречаются на практике (см. упражнение 13.14).
Еще один потенциальный недостаток рандомизированных BST-деревьев — необходимость наличия в каждом узле поля количества узлов в его поддереве. В больших деревьях дополнительный объем памяти для размещения этого поля может оказаться чрезмерной платой. С другой стороны, как было показано в "Таблицы символов и деревья бинарного поиска" , это поле может требоваться и по ряду других причин — например, для поддержки операции выбрать или для обеспечения проверки целостности структуры данных. В подобных случаях рандомизированные BST-деревья не требуют дополнительных затрат памяти, и их использование становится весьма привлекательным.
Основной принцип сохранения случайности в деревьях приводит также к эффективным реализациям операций удалить, объединить и других операций АТД таблицы символов, обеспечивая при этом создание случайных деревьев.
Для объединения дерева из N узлов с деревом из M узлов используется базовый метод, описанный в "Таблицы символов и деревья бинарного поиска" , за исключением принятия случайного решения о выборе корня по принципу: корень объединенного дерева выбирается из дерева с N узлами с вероятностью N/(M + N), а из дерева с М узлами — с вероятностью M/ (M + N). В программе 13.3 приведена реализация этой операции.
Аналогично произвольное решение можно заменить случайным и в алгоритме операции удалить, как показано в программе 13.4. Этот метод соответствует варианту удаления узлов в стандартных BST-деревьях, который не был нами рассмотрен, поскольку без рандомизации он приводил бы к несбалансированным деревьям (см. упражнение 13.21).
Программа 13.3. Объединение рандомизированных BST-деревьев
В данной функции используется тот же подход, что и в программе 12.17, за исключением того, что в ней принимается не произвольное, а случайное решение о том, какой узел использовать в качестве корня объединенного дерева, исходя из равной вероятности помещения в корень любого узла. Приватная функция-член fixN заносит в b->N значение, которое на 1 больше суммы соответствующих полей в поддеревьях (0 для пустых деревьев).
private:
link joinR(link a, link b)
{ if (a == 0) return b;
if (b == 0) return a;
insertR(b, a->item);
b->l = joinR(a->l, b->l);
b->r = joinR(a->r, b->r);
delete a; fixN(b); return b;
}
public:
void join(ST<Item, Key>& b)
{ int N = head->N;
if (rand()/(RAND MAX/(N+b.head->N)+1) < N)
head = joinR(head, b.head);
else
head = joinR(b.head, head);
}
Программа 13.4. Удаление в рандомизированном BST-дереве
Для удаления используется та же функция remove, что и для стандартных BST-деревьев (см. программу 12.16), но функция joinLR заменена приведенной здесь функцией. В ней принимается не произвольное, а случайное решение, заменить ли удаляемый узел предком или потомком, исходя из того, что каждый узел в результирующем дереве с равной вероятностью может быть его корнем. Чтобы счетчики узлов содержали правильные значения, в качестве последнего оператора в функции removeR нужен вызов функции fixN (см. программу 13.3) для h.
link joinLR(link a, link b)
{ if (a == 0) return b;
if (b == 0) return a;
if (rand()/(RAND_MAX/(a->N+b->N)+1) < a->N)
{ a->r = joinLR(a->r, b); return a; }
else
{ b->l = joinLR(a, b->l); return b; }
}
Лемма 13.3. Создание дерева с помощью произвольной последовательности случайных операций вставить, удалить и объединить эквивалентно построению стандартного BST-дерева из случайной перестановки ключей дерева.
Как и в случае с леммой 13.1, для доказательства этого утверждения требуется тщательный вероятностный анализ (см. раздел ссылок). 
Доказательства свойств вероятностных алгоритмов требуют хорошего понимания теории вероятностей, но понимание таких доказательств отнюдь не обязательно для программистов, использующих эти алгоритмы. Осмотрительный программист в любом случае проверит утверждения, подобные свойству 13.3, независимо от того, как они обоснованы (например, проверив качество генератора случайных чисел или иных особенностей реализации), и, следовательно, сможет уверенно использовать эти методы. Похоже, что рандомизированные BST-деревья представляют собой простейший способ поддержки всех свойств АТД таблицы символов при гарантии почти оптимальной производительности — именно поэтому они находят применение во многих практических приложениях.
Упражнения
13.8. Нарисуйте рандомизированное BST-дерево, образованное вставками элементов с ключами E A S Y Q U T I O N в указанном порядке в первоначально пустое дерево, если реализован плохой метод рандомизации, выполняющий вставку в корень каждый раз при нечетном размере дерева.
13.9. Напишите программу-драйвер, которая 1000 раз выполняет следующий эксперимент для N = 10 и 100: используя программу 13.2, вставляет ключи от 0 до N — 1 (по порядку) в первоначально пустое рандомизированное BST-дерево, а затем выводит 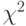 -распределение для предположения, что вероятность попадания каждого ключа в корень равна 1/N (см. упражнение 14.5).
-распределение для предположения, что вероятность попадания каждого ключа в корень равна 1/N (см. упражнение 14.5).
13.10. Приведите вероятность попадания ключа F в каждую из позиций, показанных на рис. 13.2.
13.11. Напишите программу вычисления вероятности того, что рандомизированная вставка завершается в одном из внутренних узлов заданного дерева, для каждого из узлов на пути поиска.
13.12. Напишите программу вычисления вероятности того, что рандомизированная вставка завершается в одном из внешних узлов заданного дерева.
13.13. Реализуйте нерекурсивную версию функции рандомизированной вставки, приведенной в программе 13.2.
13.14. Нарисуйте рандомизированное BST-дерево, образованное вставками элементов с ключами E A S Y Q U T I O N в указанном порядке в первоначально пустое дерево при использовании версии программы 13.2, в которой в выражении, принимающем решение о применении вставки в корень, вызов rand() заменен проверкой (111 % h.N) == 3.
13.15. Выполните упражнение 13.9 для версии программы 13.2, в которой в выражении, принимающем решение о применении вставки в корень, вызов rand() заменен проверкой (111 % h.N) == 3.
13.16. Приведите последовательность случайных решений, которая привела бы к построению вырожденного дерева (все ключи упорядочены, а левые ссылки являются пустыми) из ключей E A S Y Q U T I O N. Какова вероятность возникновения этого события?
13.17. Может ли любое BST-дерево, содержащее ключи E A S Y Q U T I O N, быть построено с помощью какой-либо последовательности случайных решений, если эти ключи вставляются в указанном порядке в первоначально пустое дерево? Обоснуйте свой ответ.
13.18. Определите эмпирическим путем среднее значение и среднеквадратичное отклонение количества сравнений, используемых для успешных и неудачных поисков в рандомизированном BST-дереве, построенном вставками N случайных ключей в первоначально пустое дерево, при N = 103, 104, 105 и 106 .
13.19. Нарисуйте BST-дерево, образованное в результате удаления программой 13.4 ключа Q из дерева, построенного в упражнении 13.14, если для принятия решения об объединении с помещением ключа a в корень используется проверка (111 % (a.N + b.N)) < a.N.
13.20. Нарисуйте BST-дерево, образованное вставками элементов с ключами E A S Y в первоначально пустое дерево, вставками элементов с ключами Q U E S T I O N в другое первоначально пустое дерево и последующим объединением результатов программой 13.3 с проверкой, описанной в упражнении 13.19.
13.21. Нарисуйте BST-дерево, образованное вставками элементов с ключами E A S Y Q U T I O N в указанном порядке в первоначально пустое дерево и последующим удалением ключа Q программой 13.4, если используется плохой генератор случайных чисел, всегда возвращающий 0.
13.22. Экспериментально определите рост высоты BST-дерева при выполнении длинной последовательности чередующихся случайных вставок и удалений с помощью программ 13.2 и 13.3 в дереве из N узлов, при N = 10, 100 и 1000 и при выполнении N2 пар вставок-удалений для каждого N.
13.23. Сравните результаты, полученные в упражнении 13.22, с результатом удаления и повторной вставки наибольшего ключа в рандомизированном дереве из N узлов с помощью программ 13.2 и 13.3, для N = 10, 100 и 1000 и при выполнении N2 пар вставок-удалений для каждого N.
13.24. Добавьте в программу из упражнения 13.22 возможность определения среднего количества вызовов функции rand() при удалении одного элемента.