Проект "Компилятор формул"
Рекурсивный компилятор формул
Как уже было отмечено в предыдущей секции, грамматика 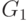 не
подходит
для использования ее в качестве базовой при реализации компилятора
формул из-за отсутствия в ней учета приоритета операций. Поэтому поставим
перед собой задачу реализовать компилятор, т.е. программу, осуществляющую
автоматический перевод с сохранением семантики, с языка
не
подходит
для использования ее в качестве базовой при реализации компилятора
формул из-за отсутствия в ней учета приоритета операций. Поэтому поставим
перед собой задачу реализовать компилятор, т.е. программу, осуществляющую
автоматический перевод с сохранением семантики, с языка  на
язык
на
язык  программ стекового калькулятора.
программ стекового калькулятора.
Задача 12.1. Напишите программу (компилятор формул), которая для любой правильной
арифметической формулы (элемента языка  ), данной ей на вход,
выдает семантически эквивалентную ей программу стекового калькулятора
(элемент языка
), данной ей на вход,
выдает семантически эквивалентную ей программу стекового калькулятора
(элемент языка  ).
).
Сначала даже не ясно, как подступиться к такой задаче. Однако ее разрешимость сомнения вызывать не должна — существуют же компиляторы с огромного множества языков программирования, включая язык Java!
Ключом к решению задачи является использование грамматик, задающих
входной и выходной языки. Существует вполне естественное соответствие между
грамматиками 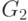 и
и 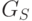 : в них обеих имеются ровно по
одному правилу,
порождающему каждую из четырех арифметических операций и правило, порождающее
имя переменной (переменная является одним из способов задания числа).
: в них обеих имеются ровно по
одному правилу,
порождающему каждую из четырех арифметических операций и правило, порождающее
имя переменной (переменная является одним из способов задания числа).
Для любой цепочки входного языка рассмотрим ее вывод в грамматике 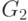 ,
а затем заменим правила входной грамматики, используемые на
каждом шаге вывода, на соответствующие им правила выходной грамматики
,
а затем заменим правила входной грамматики, используемые на
каждом шаге вывода, на соответствующие им правила выходной грамматики 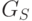 .
В результате у нас получится цепочка выходного языка, которая будет иметь
тот же самый смысл, что и входная цепочка.
.
В результате у нас получится цепочка выходного языка, которая будет иметь
тот же самый смысл, что и входная цепочка.
Попробуем реализовать данную общую идею, применив рекурсию. Это определяет имя компилятора, который будет построен — рекурсивный компилятор формул.
Будем трактовать поставленную задачу следующим образом: реализовать
класс RecursCompf с методом compile, получающим в качестве
аргумента исходную формулу (цепочку языка  ) в виде массива
символов,
который компилирует эту формулу и печатает получившийся результат (цепочку
языка
) в виде массива
символов,
который компилирует эту формулу и печатает получившийся результат (цепочку
языка  . Метод main, предназначенный для тестирования
получившейся программы реализуем в отдельном классе RecursCompfTest.
Для ввода/вывода информации будем использовать методы класса Xterm,
а весь исходный текст программы разместим в одном файле, который будет
иметь имя RecursCompfTest.java.
. Метод main, предназначенный для тестирования
получившейся программы реализуем в отдельном классе RecursCompfTest.
Для ввода/вывода информации будем использовать методы класса Xterm,
а весь исходный текст программы разместим в одном файле, который будет
иметь имя RecursCompfTest.java.
После завершения работы над программой она должна вести себя примерно так:
[roganov@msiu compf]$ java RecursCompfTest Введите формулу -> a a Введите формулу -> a-b a b - Введите формулу -> (a-b)*(a+b) a b - a b + *
Приступим собственно к решению. Создадим отдельный метод для обработки
каждого из четырех метасимволов грамматики 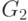 . Для компиляции
формулы
(метасимвола
. Для компиляции
формулы
(метасимвола  ) будем использовать метод compileF, терма — compileT, множителя — compileM, а имени переменной —
метод compileV. Так как любая цепочка входного языка
представляет из себя формулу, что соответствует метасимволу
) будем использовать метод compileF, терма — compileT, множителя — compileM, а имени переменной —
метод compileV. Так как любая цепочка входного языка
представляет из себя формулу, что соответствует метасимволу  грамматики
грамматики 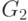 , то ее компиляция, выполняемая методом compile, должна
сводится к
вызову метода compileF.
, то ее компиляция, выполняемая методом compile, должна
сводится к
вызову метода compileF.
В соответствии с первым правилом грамматики 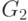 формула всегда
начинается
с терма. Таким образом, первое действие, которое должен выполнить метод compileF, — это вызвать метод compileT. Опять таки в соответствии
с грамматикой далее возможны три различных варианта: либо формула
на этом заканчивается (сводится просто к терму), либо за знаками сложения или
вычитания (два варианта) следует еще одна формула.
формула всегда
начинается
с терма. Таким образом, первое действие, которое должен выполнить метод compileF, — это вызвать метод compileT. Опять таки в соответствии
с грамматикой далее возможны три различных варианта: либо формула
на этом заканчивается (сводится просто к терму), либо за знаками сложения или
вычитания (два варианта) следует еще одна формула.
Теперь уже в соответствии с грамматикой 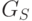 можно сделать
вывод о том, как
должна происходить работа метода compileF в каждом из этих трех случаях.
В первом из них делать ничего не надо, а в двух остальных следует сначала обработать формулу, следующую за знаком операции, а затем
напечатать символ, ей соответствующий ( + или - ).
можно сделать
вывод о том, как
должна происходить работа метода compileF в каждом из этих трех случаях.
В первом из них делать ничего не надо, а в двух остальных следует сначала обработать формулу, следующую за знаком операции, а затем
напечатать символ, ей соответствующий ( + или - ).
Обратите внимание, что при такой реализации метод compileF не пытается
откомпилировать всю полученную методом compile формулу целиком —
им обрабатывается только некоторая ее часть, соответствующая одному метасимволу  в процессе ее вывода.
в процессе ее вывода.
Для того чтобы можно было реализовать описанную идею, необходимо конкретизировать форму представления исходной формулы. Так как метод compile получает ее в виде массива символов str, вполне естественно сделать этот массив private -компонентой класса RecursCompf, доступной всем его методам и с помощью еще одной private -компоненты index отслеживать ту часть формулы, которая уже обработана. Обработка завершается, когда достигается конец формулы, длина которой равна str.length.
Этого вполне достаточно для реализации метода compileF:
private void compileF() {
compileT();
if (index >= str.length) return;
if (str[index] == '+'){
index++;
compileF();
Xterm.print("+ ");
return;
}
if (str[index] == '-'){
index++;
compileF();
Xterm.print("- ");
}
}Обработка терма совершенно аналогична обработке формулы — это следует из
грамматик 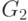 и
и 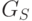 , поэтому метод compileT
пишется мгновенно:
, поэтому метод compileT
пишется мгновенно:
private void compileT() {
compileM();
if (index >= str.length) return;
if (str[index] == '*'){
index++;
compileT();
Xterm.print("* ");
return;
}
if (str[index] == '/'){
index++;
compileT();
Xterm.print("/ ");
}
}Множитель  в грамматике
в грамматике 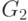 является либо
заключенной в скобки формулой,
либо именем переменной. В первом случае необходимо пропустить открывающую
скобку, затем вызвать метод compileF и пропустить закрывающую скобку,
а во втором достаточно просто вызвать метод обработки имени переменной:
является либо
заключенной в скобки формулой,
либо именем переменной. В первом случае необходимо пропустить открывающую
скобку, затем вызвать метод compileF и пропустить закрывающую скобку,
а во втором достаточно просто вызвать метод обработки имени переменной:
private void compileM() {
if (str[index] == '(') {
index++;
compileF();
index++;
} else compileV();
}Последний из оставшихся методов является самым простым — обработка имени переменной сводится к печати этого имени (и перемещению указателя index ):
private void compileV() {
Xterm.print("" + str[index++] + " ");
}Полный текст построенной программы приведен в последней секции параграфа, а мы сейчас попробуем ответить на стандартный для рекурсивных программ вопрос: почему эта программа заканчивает работу? Потенциально опасными в данном случае являются методы compileF и compileT, которые являются рекурсивными. Перед каждым таким рекурсивным вызовом, однако, обработанная часть исходной формулы увеличивается (возрастает значение переменной index ), что, в силу конечности длины исходной формулы, и гарантирует завершение работы программы в целом.
Сделаем одно небольшое чисто технологическое замечание. Хотя построенная нами реализация и является достаточно простой, программа в целом использует три различных файла ( RecursCompfTest.java, RecursCompf.java и Xterm.java ), размещенных в двух директориях (каталогах). Хорошим средством для автоматизации работы над сложными программными проектами является утилита make, которая позволяет значительно облегчить труд программиста в процессе написания и отладки большой программы (на любом языке).
В специальном управляющем файле, обычно именуемом Makefile, необходимо указать те конечные и промежуточные цели, которые должны быть достигнуты в процессе работы над проектом. В нашем случае такими целями являются запуск итоговой программы, ее компиляция и удаление class -файлов. Каждой цели в управляющем файле дается уникальное имя, после которого ставится двоеточие и перечисляются те файлы, от которых данная цель зависит, а в следующей строке после обязательного символа табуляции записывается действие, которое должно быть выполнено для достижения цели.
Когда утилита make запускается с указанием одной из перечисленных в управляющем файле целей в виде ее аргумента, то все необходимые действия для достижения цели выполняются автоматически. При этом выясняется, не изменились ли некоторые из файлов, от которых зависит цель. Если это произошло, то все промежуточные цели, от них зависящие, также будут заново перестроены. При запуске make без указания аргумента в качестве цели берется первая из встречающихся в управляющем файле.
Вот полный текст управляющего файла, который используется в рассматриваемом проекте:
Makefile
# -*- mode: makefile -*-
.PHONY : run clean
# Запустить тест рекурсивного компилятора формул.
run: RecursCompfTest.class
java RecursCompfTest
# Откомпилировать текст рекурсивного компилятора формул.
RecursCompfTest.class: RecursCompfTest.java RecursCompf.java \
Xterm.java
javac RecursCompfTest.java
# Удалить лишние файлы.
clean:
rm -f *.class *.expandКроме описания трех целей ( run, RecursCompfTest.class и clean ) в нем содержится информация для редактора emacs о специальном режиме работы с этим файлом и указание для утилиты make, сообщающее, что цели run и clean относятся к разряду особых — они не является именами файлов, создаваемых при их построении. Символ \ в конце строки означает, что следующая строка файла должна рассматриваться, как продолжение предыдущей.
Команда make, которая в данном случае эквивалентна make run, сначала выяснит, нет ли уже построенной цели RecursCompfTest.class. Если она существует и времена модификации всех файлов, от которых зависит эта цель ( RecursCompfTest.java, RecursCompf.java и Xterm.java ) не превосходят времени создания цели RecursCompfTest.class, то будет просто выполнена команда запуска java RecursCompfTest. Если же хотя бы один из файлов с исходными текстами был модифицирован, то произойдет его перекомпиляция.
Утилита make, таким образом, позволяет не заботиться о перекомпиляции измененных исходных файлов, выполняя ее автоматически.
Следующее замечание касается поведения построенной нами программы при работе с некорректными формулами. При попытке откомпилировать с ее помощью подобную формулу поведение программы является непредсказуемым. Это, однако, вполне соответствует ее спецификации — программа должна была компилировать только правильные формулы.
И еще одно замечание. При компиляции формулы 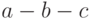 получается
результат a b c - -, что явно не верно!. Правильным результатом является a b - c -. Значит написанная нами программа ошибочна?
получается
результат a b c - -, что явно не верно!. Правильным результатом является a b - c -. Значит написанная нами программа ошибочна?
На самом деле программа написана абсолютно правильно, а причина неверной
компиляции заключается в грамматике 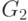 . Дело в том, что эта
грамматика,
верно отражая приоритеты арифметических операций, неявно считает их все правоассоциативными, в то время как они являются на самом деле левоассоциативными. Это хорошо видно из рисунка 12.3,
где изображено дерево вывода формулы
. Дело в том, что эта
грамматика,
верно отражая приоритеты арифметических операций, неявно считает их все правоассоциативными, в то время как они являются на самом деле левоассоциативными. Это хорошо видно из рисунка 12.3,
где изображено дерево вывода формулы 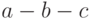 в грамматике
в грамматике 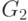 .
.
Определенная выше грамматика 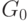 , задавая тот же язык,
предполагает
правильную ассоциативность операций. К сожалению, использовать ее для написания
рекурсивного компилятора формул нельзя. При обработке формулы совершенно
не ясно, с чего она начинается — с терма или с формулы. Кроме того,
рекурсивная цепочка вызовов в данном случае вполне может оказаться
бесконечной.
, задавая тот же язык,
предполагает
правильную ассоциативность операций. К сожалению, использовать ее для написания
рекурсивного компилятора формул нельзя. При обработке формулы совершенно
не ясно, с чего она начинается — с терма или с формулы. Кроме того,
рекурсивная цепочка вызовов в данном случае вполне может оказаться
бесконечной.
Одним из способов построения компилятора, который будет учитывать
левоассоциативность всех арифметических операций, является использование
грамматики  . Основываясь на ней, можно построить другую
реализацию
рекурсивного компилятора формул, в которой метод compileF после
вызова метода обработки терма будет содержать цикл, обеспечивающий обработку
всех следующих за ним других термов этой формулы. Аналогичное изменение
необходимо сделать и в методе compileT.
. Основываясь на ней, можно построить другую
реализацию
рекурсивного компилятора формул, в которой метод compileF после
вызова метода обработки терма будет содержать цикл, обеспечивающий обработку
всех следующих за ним других термов этой формулы. Аналогичное изменение
необходимо сделать и в методе compileT.
Такая реализация компилятора будет уже корректно обрабатывать все
правильные
арифметические формулы. Ее основной недостаток — невозможность простой
модификации. Внесение даже небольших изменений во входной язык требует
внесения глобальных изменений и переписывания значительной части программы.
Примером подобного изменения может быть повышение приоритета вычитания так,
что формула  должна будет трактоваться, как
должна будет трактоваться, как  .
.
Для построения достаточно гибкой реализации компилятора формул целесообразно применить совсем иной подход.

