Проект "Компилятор формул"
Стековый компилятор формул
Напомним, что компилятор  представляет собой программную
реализацию
отображения из множества цепочек одного языка в множество цепочек другого.
По этой причине его можно рассматривать, как функцию на пространстве
последовательностей. Легко понять, что в рассматриваемом случае перевода
с языка правильных арифметических формул на язык программ для стекового
калькулятора эта функция не индуктивна.
представляет собой программную
реализацию
отображения из множества цепочек одного языка в множество цепочек другого.
По этой причине его можно рассматривать, как функцию на пространстве
последовательностей. Легко понять, что в рассматриваемом случае перевода
с языка правильных арифметических формул на язык программ для стекового
калькулятора эта функция не индуктивна.
Для доказательства этого факта применим отрицание критерия индуктивности.
Результатом компиляции цепочек  и
и 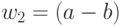 является
одна и та же цепочка a b -.
Если дописать к обеим этим цепочкам
двухэлементную цепочку
является
одна и та же цепочка a b -.
Если дописать к обеим этим цепочкам
двухэлементную цепочку  (любая одноэлементная приводит к
неправильной
формуле), то результатом компиляции первой из них будет программа a b c * -, a второй — a b - c *, т.е.
(любая одноэлементная приводит к
неправильной
формуле), то результатом компиляции первой из них будет программа a b c * -, a второй — a b - c *, т.е.  .
.
Попробуем построить индуктивное расширение  функции
функции  так,
чтобы с его
помощью реализовать однопроходный алгоритм, осуществляющий нужный нам перевод.
Прежде всего заметим, что любую правильную формулу можно откомпилировать так,
что, во-первых, переменные в выходной цепочке (программе для стекового
калькулятора) будут идти в том же порядке, что и переменные в исходной
формуле;
и, во-вторых, все операции в выходной цепочке будут расположены позже
соответствующих им операций в исходной формуле.
так,
чтобы с его
помощью реализовать однопроходный алгоритм, осуществляющий нужный нам перевод.
Прежде всего заметим, что любую правильную формулу можно откомпилировать так,
что, во-первых, переменные в выходной цепочке (программе для стекового
калькулятора) будут идти в том же порядке, что и переменные в исходной
формуле;
и, во-вторых, все операции в выходной цепочке будут расположены позже
соответствующих им операций в исходной формуле.
Доказательство этого утверждения можно провести с помощью индукции по числу операций в исходной формуле. База индукции (случай полного отсутствия операций) проверяется непосредственно, а индуктивный переход осуществляется следующим рассуждением.
Пусть сформулированное выше утверждение справедливо для любой формулы, число
операций в которой не превосходит  . Рассмотрим произвольную
формулу с
. Рассмотрим произвольную
формулу с  операцией. Выделим ту из этих операций, которая должна
выполняться
последней в соответствии с действующими приоритетами и ассоциативностью.
Данная операция разделяет два фрагмента исходной формулы, в каждом из которых
содержится не более, чем по
операцией. Выделим ту из этих операций, которая должна
выполняться
последней в соответствии с действующими приоритетами и ассоциативностью.
Данная операция разделяет два фрагмента исходной формулы, в каждом из которых
содержится не более, чем по  операций. По предположению индукции
каждый из
них может быть откомпилирован с соблюдением двух сформулированных выше условий.
Запишем последовательно результат компиляции каждого из них, а затем —
символ выделенной операции. Получившаяся цепочка, являющаяся переводом исходной
формулы, удовлетворяет нужным требованиям, что и завершает доказательство.
операций. По предположению индукции
каждый из
них может быть откомпилирован с соблюдением двух сформулированных выше условий.
Запишем последовательно результат компиляции каждого из них, а затем —
символ выделенной операции. Получившаяся цепочка, являющаяся переводом исходной
формулы, удовлетворяет нужным требованиям, что и завершает доказательство.
Таким образом, формулу можно компилировать так: встретив имя переменной,
немедленно его печатать, а встретив знак операции или скобку, печатать
те из предыдущих, но еще не обработанных операций (будем их называть отложенными ), которые выполнимы в данный момент, после чего
"откладывать" и новый знак. Поскольку в любой момент времени среди
отложенных операций нет таких, которые выполнимы до только что пришедшего
знака, то в качестве контейнера для хранения отложенных операций можно
использовать стек. Этот стек и будет содержать ту дополнительную информацию,
которая необходима для индуктивного перевычисления функции  ,
осуществляющей компиляцию исходной формулы.
,
осуществляющей компиляцию исходной формулы.
Требуемый нам класс Compf, содержащий метод compile, можно сделать выведенным из класса Stack, являющегося непрерывной реализацией стека символов на базе вектора. Как это было объяснено выше, метод compile должен обеспечивать последовательную обработку всех символов исходной формулы, что будет осуществляться с помощью private -метода processSymbol.
В момент появления в формуле правой скобки необходимо выполнить все отложенные, но еще не выполненные операции, содержащиеся в стеке. То же самое нужно сделать и тогда, когда формула закончится. Для того, чтобы не различать эти две ситуации можно взять в скобки исходную формулу, что и реализовано в методе compile:
public void compile(char[] str) {
processSymbol('(');
for(int i = 0; i < str.length; i++)
processSymbol(str[i]);
processSymbol(')');
Xterm.print("\n");
}Все возможные входные символы делятся (с помощью метода symType ) на четыре категории: две скобки ( SYM\_LEFT и SYM\_RIGHT ), знаки операций ( SYM\_OPER ) и все остальные ( SYM\_OTHER ). К последним относятся, прежде всего, имена переменных.
Реализация метода processSymbol полностью соответствует проведенному выше обсуждению компиляции с помощью стека:
private void processSymbol(char c) {
switch (symType(c)) {
case SYM_LEFT:
push(c); break;
case SYM_RIGHT:
processSuspendedSymbols(c); pop(); break;
case SYM_OPER:
processSuspendedSymbols(c); push(c); break;
case SYM_OTHER:
nextOther(c); break;
}
}Открывающая скобка всегда заносится в стек отложенных операций; закрывающая скобка приводит к вызову метода processSuspendedSymbols, обрабатывающего отложенные символы, и удалению из стека парной ей открывающей скобки; символ операции вызывает обработку отложенных символов и сам затем помещается в стек; а имя переменной просто печатается с помощью методов nextOther и nextOper.
Метод processSuspendedSymbols обеспечивает обработку всех тех отложенных операций, которые выполнимы в данный момент, что определяется приоритетом операций (метод priority ) и правилами предшествования (метод precedes ):
private void processSuspendedSymbols(char c) {
while (precedes(top(), c))
nextOper(pop());
}
private int priority(char c) {
return c == '+' || c == '-' ? 1 : 2;
}
private boolean precedes(char a, char b) {
if(symType(a) == SYM_LEFT) return false;
if(symType(b) == SYM_RIGHT) return true;
return priority(a) >= priority(b);
}
protected void nextOper(char c) {
Xterm.print("" + c + " ");
}Текст проекта целиком приведен в последней секции параграфа. Обратите внимание, насколько эта реализация компилятора сложнее рекурсивной. Однако она позволяет легко модифицировать ее при изменении входного языка. Например, изменение ассоциативности всех арифметических операций требует только удаления одного символа: в методе precedes нужно >= заменить на >. Многие значительно более сложные задачи на модификацию также сводятся к минимальным изменениям в тексте программы и не требует изменения структуры всей реализации в целом.
Так же, как и построенный ранее рекурсивный компилятор формул, стековый компилятор не делает никаких попыток сообщить о характере и месторасположении ошибки в некорректной формуле, данной ему на вход. Это отличает его от реально используемых компиляторов, в которых анализ ошибок во входной программе и выдача максимально полной информации о них является одной из важнейших задач. Причем зачастую эта задача ничуть не проще, нежели основная задача компилятора — осуществление перевода на выходной язык.
Использование в тексте программы ключевого слова protected и некоторые другие не вполне понятные моменты объясняются тем, что построенный класс Compf будет использован в качестве базового для реализации интерпретатора арифметических выражений. Подобный подход является характерной особенностью объектно-ориентированного программирования — уже написанный код может быть использован для решения родственной задачи без какой-либо его модификации.
