| Россия |
Предобработка данных
Понижение размерности входов
Сильной стороной нейроанализа является возможность получения предсказаний при минимуме априорных знаний. Поскольку заранее обычно
неизвестно насколько полезны те или иные входные переменные для предсказания значений выходов, возникает соблазн увеличивать число
входных параметров, в надежде на то, что сеть сама определит какие из них наиболее значимы. Однако, как это уже обсуждалось в
"Обучение с учителем: Распознавание образов"
,
сложность обучения персептронов быстро возрастает с ростом числа входов (а именно - как куб размерности входных данных  ). Еще важнее,
что с увеличением числа входов страдает и точность предсказаний, т.к. увеличение числа весов в сети снижает предсказательную способность
последней (согласно предыдущим оценкам:
). Еще важнее,
что с увеличением числа входов страдает и точность предсказаний, т.к. увеличение числа весов в сети снижает предсказательную способность
последней (согласно предыдущим оценкам:  ).
).
Таким образом, количество входов приходится довольно жестко лимитировать, и выбор наиболее информативных входных переменных представляет важный этап подготовки данных для обучения нейросетей. Лекция 4 специально посвящена использованию для этой цели самих нейросетей, обучаемых без учителя. Не стоит, однако, пренебрегать и традиционными, более простыми и зачастую весьма эффективными методами линейной алгебры.
Один из наиболее простых и распространенных методов понижения размерности - использование главных компонент входных векторов. Этот метод позволяет не отбрасывая конкретные входы учитывать лишь наиболее значимые комбинации их значений.
Понижение размерности входов методом главных компонент
Собственные числа матрицы ковариаций 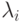 , фигурировавшие в предыдущем разделе, являются квадратами дисперсий вдоль ее главных осей.
Если между входами существует линейная зависимость, некоторые из этих собственных чисел стремятся к нулю. Таким образом, наличие малых
, фигурировавшие в предыдущем разделе, являются квадратами дисперсий вдоль ее главных осей.
Если между входами существует линейная зависимость, некоторые из этих собственных чисел стремятся к нулю. Таким образом, наличие малых 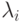 свидетельствует о том, что реальная размерность входных данных объективно ниже, чем число входов. Можно задаться некоторым пороговым
значением
свидетельствует о том, что реальная размерность входных данных объективно ниже, чем число входов. Можно задаться некоторым пороговым
значением  и ограничиться лишь теми главными компонентами, которые имеют
и ограничиться лишь теми главными компонентами, которые имеют 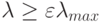 . Тем самым, достигается понижение размерности входов, при
минимальных потерях точности представления входной информации.
. Тем самым, достигается понижение размерности входов, при
минимальных потерях точности представления входной информации.
Восстановление пропущенных компонент данных
Главные компоненты оказываются удобным инструментом и для восстановления пропусков во входных данных. Действительно, метод главных
компонент дает наилучшее линейное приближение входных данных меньшим числом компонент:  (Здесь мы, как и прежде, для учета постоянного
члена включаем фиктивную нулевую компоненту входов, всегда равную единице - см.
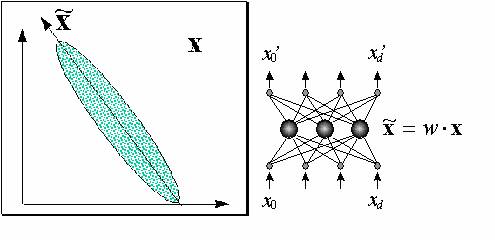
рисунок 7.5, где справа показана нейросетевая интерпретация метода главных компонент. Таким образом,
- это матрица размерности
(Здесь мы, как и прежде, для учета постоянного
члена включаем фиктивную нулевую компоненту входов, всегда равную единице - см.
рисунок 7.5, где справа показана нейросетевая интерпретация метода главных компонент. Таким образом,
- это матрица размерности 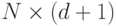 ). Восстановленные по главным компонентам данные из обучающей выборки
). Восстановленные по главным компонентам данные из обучающей выборки 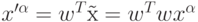 имеют наименьшее среднеквадратичное
отклонение от своих прототипов
имеют наименьшее среднеквадратичное
отклонение от своих прототипов 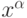 . Иными словами, при отсутствии у входного вектора
. Иными словами, при отсутствии у входного вектора  компонент, наиболее вероятное положение этого
вектора - на гиперплоскости первых
компонент, наиболее вероятное положение этого
вектора - на гиперплоскости первых 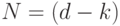 главных компонент. Таким образом, для восстановленного вектора имеем:
главных компонент. Таким образом, для восстановленного вектора имеем:  , причем для известных
компонент
, причем для известных
компонент  .
.
Пусть, например, у вектора 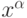 неизвестна всего одна,
неизвестна всего одна,  -я координата. Ее значение находится из оставшихся по формуле:
-я координата. Ее значение находится из оставшихся по формуле:
![x^{\prime\alpha}_k=[w^Tw]_{ki}x^\alpha_i/(1-[w^Tw]_kk),](/sites/default/files/tex_cache/9dc451d1bbe6577f0b3651ec7d9211d0.png)
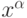 .
.В общем случае восстановить неизвестные компоненты (с индексами из множества  ) можно с помощью следующей итеративной процедуры
(см. рисунок 7.6):
) можно с помощью следующей итеративной процедуры
(см. рисунок 7.6):

 ,
,