| Россия |
Предобработка данных
Вытапливай воск, но сохраняй мед. Козьма Прутков
Мелочи не играют решающей роли. Они решают все. Х.Маккей, "Как уцелеть среди акул"
Необходимые этапы нейросетевого анализа
Теперь, после знакомства с базовыми принципами нейросетевой обработки, можно приступать к практическим применениям полученных знаний для решения конкретных задач. Первое, с чем сталкивается пользователь любого нейропакета - это необходимость подготовки данных для нейросети. До сих пор мы не касались этого, вообще говоря, непростого вопроса, молчаливо предполагая, что данные для обучения уже имеются и представлены в виде, доступном для нейросети. На практике же именно предобработка данных может стать наиболее трудоемким элементом нейросетевого анализа. Причем, знание основных принципов и приемов предобработки данных не менее, а может быть даже более важно, чем знание собственно нейросетевых алгоритмов. Последние как правило, уже "зашиты" в различных нейроэмуляторах, доступных на рынке. Сам же процесс решения прикладных задач, в том числе и подготовка данных, целиком ложится на плечи пользователя. Данная лекция призвана заполнить этот пробел в описании технологии нейросетевого анализа.
Для начала выпишем с небольшими комментариями всю технологическую цепочку, т.е. необходимые этапы нейросетевого анализа1В предположении, что задача определена и база данных для обучения нейросети уже собрана
- Кодирование входов-выходов: нейросети могут работать только с числами.
- Нормировка данных:результаты нейроанализа не должны зависеть от выбора единиц измерения.
- Предобработка данных:удаление очевидных регулярностей из данных облегчает нейросети выявление нетривиальных закономерностей.
- Обучение нескольких нейросетей с различной архитектурой: результат обучения зависит как от размеров сети, так и от ее начальной конфигурации.
- Отбор оптимальных сетей: тех, которые дадут наименьшую ошибку предсказания на неизвестных пока данных.
- Оценка значимости предсказаний: оценка ошибки предсказаний не менее важна, чем само предсказанное значение.
Если до сих пор мы ограничивали наше рассмотрение, в основном, последними этапами, связанными с обучением собственно нейросетей, то в этой лекции мы сосредоточимся на первых этапах нейросетевого анализа - предобработке данных. Хотя перебработка не связана непосредственно с нейросетями, она является одним из ключевых элементов этой информационной технологии. Успех обучения нейросети может решающим образом зависеть от того, в каком виде представлена информация для ее обучения.
В этой лекции мы рассмотрим предобработку данных для обучения с учителем и постараемся, главным образом, выделить и проиллюстрировать на конкретных примерах основной принцип такой предобработки: увеличение информативности примеров для повышения эффективности обучения.
Кодирование входов-выходов
В отличие от обычных компьютеров, способных обрабатывать любую символьную информацию, нейросетевые алгоритмы работают только с числами, ибо их работа базируется на арифметических операциях умножения и сложения. Именно таким образом набор синаптических весов определяет ход обработки данных.
Между тем, не всякая входная или выходная переменная в исходном виде может иметь численное выражение. Соответственно, все такие переменные следует закодировать - перевести в численную форму, прежде чем начать собственно нейросетевую обработку. Рассмотрим, прежде всего основной руководящий принцип, общий для всех этапов предобработки данных.
Максимизация энтропии как цель предобработки
Допустим, что в результате перевода всех данных в числовую форму и последующей нормировки все входные и выходные переменные отображаются в единичном кубе. Задача нейросетевого моделирования - найти статистически достоверные зависимости между входными и выходными переменными. Единственным источником информации для статистического моделирования являются примеры из обучающей выборки. Чем больше бит информации принесет каждый пример - тем лучше используются имеющиеся в нашем распоряжении даные.
Рассмотрим произвольную компоненту нормированных (предобработанных) данных: 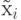 . Среднее количество информации, приносимой
каждым примером
. Среднее количество информации, приносимой
каждым примером 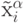 , равно энтропии распределения значений этой компоненты
, равно энтропии распределения значений этой компоненты  . Если эти значения сосредоточены в относительно небольшой
области единичного интервала, информационное содержание такой компоненты мало. В пределе нулевой энтропии, когда все значения переменной
совпадают, эта переменная не несет никакой информации. Напротив, если значения переменной
. Если эти значения сосредоточены в относительно небольшой
области единичного интервала, информационное содержание такой компоненты мало. В пределе нулевой энтропии, когда все значения переменной
совпадают, эта переменная не несет никакой информации. Напротив, если значения переменной 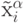 равномерно распределены в единичном
интервале, информация такой переменной максимальна.
равномерно распределены в единичном
интервале, информация такой переменной максимальна.
Общий принцип предобработки данных для обучения, таким образом, состоит в максимизации энтропии входов и выходов. Этим принципом следует руководствоваться и на этапе кодирования нечисловых переменных.
Типы нечисловых переменных
Можно выделить два основных типа нечисловых переменных: упорядоченные (называемые также ординальными - от англ. order - порядок) и
категориальные. В обоих случаях переменная относится к одному из дискретного набора классов 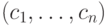 . Но в первом случае эти классы
упорядочены - их можно ранжировать:
. Но в первом случае эти классы
упорядочены - их можно ранжировать:  , тогда как во втором такая упорядоченность отсутствует. В качестве примера упорядоченных
переменных можно привести сравнительные категории: плохо - хорошо - отлично, или медленно - быстро. Категориальные переменные просто
обозначают один из классов, являются именами категорий. Например, это могут быть имена людей или названия цветов: белый, синий,
красный.
, тогда как во втором такая упорядоченность отсутствует. В качестве примера упорядоченных
переменных можно привести сравнительные категории: плохо - хорошо - отлично, или медленно - быстро. Категориальные переменные просто
обозначают один из классов, являются именами категорий. Например, это могут быть имена людей или названия цветов: белый, синий,
красный.
