Нейросетевая оптимизация

Нейросетевая оптимизация и другие "биологические "методы

Преимущества и недостатки нейросетевой оптимизации познаются в сравнении с другими развитыми в настоящее время методами. Из методов, которые иногда дают аналогичные, а порой и лучшие результаты, отметим генетические и эволюционные алгоритмы (Fogel, 1993), а также метод муравьиных колоний (Dorigo & Gambardella, 1996).

В этом разделе мы очень кратко остановимся на них, поскольку эти подходы, так же как и нейросети, используют ясные и плодотворные биологические аналогии. Кроме того, генетические алгоритмы широко используются и для обучения нейронных сетей самих по себе, поскольку обучение нейросетей связано с минимизацией функционала ошибки.

Генетические алгоритмы

Эти алгоритмы могут использоваться для поиска экстремума нелинейных функций с множественными локальными минимумами. Они имитируют адаптацию живых организмов к внешним условиям в ходе эволюции. Точнее, они моделируют эволюцию целых популяций организмов и поэтому требуют достаточно больших ресурсов памяти и высокой скорости вычислительных систем. Важным достоинством их является то, что они не накладывают никаких требований на вид минимизируемой функции (например, дифференцируемость). Поэтому их можно применять в случаях, когда градиентные методы не применимы.

Генетические алгоритмы используют соответствующую терминологию, конфигурации системы называют хромосомами, над которой можно производить операции кроссинговера и мутации. Хромосома является основной информационной единицей, кодирующей переменную, относительно которой ищется оптимум. Обычно она представляет собой битовую строку, хотя компоненты этой строки могут иметь и более общий вид (для задачи коммивояжера компоненты хромосом представляют собой последовательность номеров городов в данном маршруте, например (145321)). Каждая компонента хромосомы называется геном. Выбор удачного представления для хромосомы, или же кодировка искомого решения, могут значительно облегчить нахождение решения.

Обучение происходит в популяции хромосом, к которым на каждом шаге эволюции применяются две основные операции. При мутациях в хромосоме случайным образом выбираются и изменяются ее компоненты (гены). При кроссинговере две хромосомы А и В разрезаются на две части в случайно выбранной одной точке 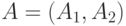и 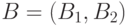и обмениваются ими, давая две новые хромосомы: и 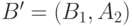(см. рисунок 6.4).

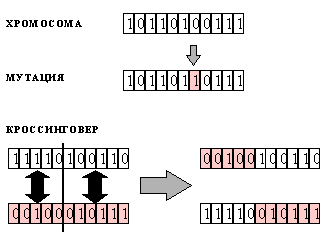
Рис. 6.4. Представление искомого решения в виде битовой строки - хромосомы (вверху). Операции мутации и кроссинговера (внизу)

После каждого шага эволюции - генерации, на котором мутируют и подвергаются кроссинговеру все хромосомы, для каждой из новых хромосом вычисляется значение целевого функционала, которое достигается на кодируемых ими решениях. Чем меньше это значение для данной хромосомы, тем с большей вероятностью она отбирается для кроссинговера. В ходе эволюции усредненное по популяции значение функционала будет уменьшаться, и после завершения процесса (проведения заданного числа генераций) хромосома с минимальным его значаением выбирается в качестве приближенного решения поставленной задачи. Можно значительно улучшить свойства генетического алгоритма если после порождения новой генерации хромосом предварительно объединить ее с предыдущей популяцией и выбрать из 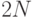полученных хромосом наилучших. Опыт показывает, что генетические алгоритмы особенно эффективны при поиске глобального оптимума, поскольку они осуществляют поиск в широком пространстве решений. Если закодировать в виде хромосом значения весов и порогов нейронной сети заданной архитектуры и использовать в роли минимизируемой функции функционал ошибки, то генетические алгоритмы можно использовать для обучения этой нейронной сети. Очевидно, что для этой же цели можно использовать и описанный ранее метод иммитации отжига.

Метод муравьиных колоний

Энтомологи установили, что муравьи способны быстро находить кратчайший путь от муравейника к источнику пищи. Более того, они могут адаптироваться к изменяющимся условиям , находя новый кратчайший путь. Рассмотрим рисунок 6.5: муравьи движутся по прямой, соединяющей муравейник с местом, в котором находится пища. При движении муравей метит свой путь специальными веществами - феромонами, и эта информация используется другими муравьями для выбора пути. А именно, муравьи предпочитают тропки наиболее обогащенные феромонами. Это элементарное правило поведения муравьев и определяет их способность находить новые пути, если старый оказывается перерезанным преградой. Действительно, достигнув этой преграды, муравьи уже не смогут продолжить свой путь и с равной вероятностью будут обходить ее справа и слева. То же самое будет происходить и на обратной стороне преграды. Однако, те муравьи, которые случайно выберут кратчайший путь (налево от преграды и направо - на обратном пути), будут быстрее проходить свой путь и он с большей скоростью станет обогащаться феромонами. Поэтому следующие муравьи будут предпочитать именно этот наикратчайший путь, метя его и далее. Очевидная положительная обратная связь быстро приведет к тому, что кратчайший путь станет единственным маршрутом движения насекомых.

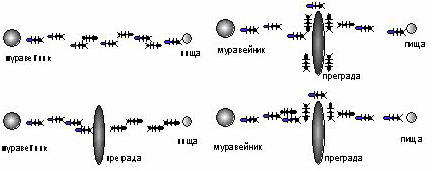
Рис. 6.5. Муравьи находят новый кратчайший новый путь (сверху от преграды) который быстрее обогащается феромонами

Подобный процесс может осуществляться и в компьютерном мире, населенном Искусственными Муравьями (ИМ). Такие муравьи могут решить и нашу задачу коммивояжера. В этом случае они движутся от города к городу по ребрам соответствующего графа. При этом они выбирают направление движения, используя вероятностную функцию, зависящую как от предыдущих попыток движения по данному ребру, так и от эвристического значения, являющегося функцией длины ребра. ИМ с большей вероятностью будут предпочитать ближайшие города и города, связанные ребрами, наиболее богатыми феромонами. Первоначально искусственных муравьев размещаются в случайно выбранных городах. В каждый последующий момент времени они перемещаются в соседние города и изменяют концентрацию феромона на своем пути (локальная модификация). После того, как все ИМ завершат движения по замкнутому маршруту, тот из них, который проделал кратчайший путь, добавляет к его звеньям количество феромона, обратно пропорциональное длине этого пути (глобальная модификация). В отличие от живых муравьев, ИМ обладают способностью определять расстояние до соседних городов и помнят, какие города они уже посетили. Оказывается, метод искусственных муравьиных колоний может давать результаты, лучшие чем при использовании имитации отжига, нейронных сетей, и генетических алгоритмов.

Напомним вновь, что при электронной или оптической реализации нейросетевой подход находится вне конкуренции в ситуациях, когда необходимо очень быстро находить не обязательно оптимальное, но достаточно хорошее решение.