| Россия |
Нейросетевая оптимизация
Оптимизация и сеть Хопфилда
В 1985г. Хопфилд и Танк предложили использовать минимизирующие энергию нейронные сети для решения задач оптимизации (Hopfield & Tank, 1985). В качестве примера они, естественно, рассмотрели задачу коммивояжера.
Для решения этой задачи с помощью нейронной сети Хопфилда нужно закодировать маршрут активностью нейронов и так подобрать связи между ними, чтобы энергия сети оказалась связанной с полной длиной маршрута. Хопфилд и Танк предложили для этого следующий способ.
Рассмотрим сеть, состоящую из  бинарных нейронов, состояния которых мы обозначим
бинарных нейронов, состояния которых мы обозначим 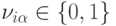
 , где индекс
, где индекс  кодирует город, а индекс
кодирует город, а индекс  -
номер города в маршруте (см.
рисунок 6.1). Если обозначить через
-
номер города в маршруте (см.
рисунок 6.1). Если обозначить через 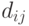 расстояние между
расстояние между  -м и
-м и  -м городами, решение задачи коммивояжера
сводится к минимизации целевой функции
-м городами, решение задачи коммивояжера
сводится к минимизации целевой функции
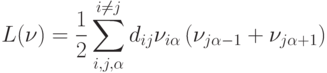
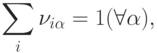
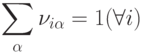
Общий подход к ограничениям в задачах оптимизации состоит в том, что в итоговый функционал, подлежащий минимизации, включаются штрафные члены, увеличивающие целевую функцию при отклонении от накладываемых ограничений. В данном случае в качестве энергии состояния сети можно выбрать функционал
![E(\nu)=\frac{1}{2}\sum^{i\neq
j}_{i,j,\alpha}d_{ij}\nu_{i\alpha}\left(\nu_{j
\alpha-1}+\nu_{j\alpha+1}\right)+\\\frac{\gamma}{2}\left[\sum_{\alpha}\left(\sum_{i}\nu_{i\alpha}-1\right)^2+\sum_{i}\left(\sum_{\alpha}\nu_{i\alpha}-1\right)^2\right],](/sites/default/files/tex_cache/a25c90b4ad73f8d7041cce4869abe277.png)
 регулирует строгость соблюдения дополнительных условий в конечном решении.
регулирует строгость соблюдения дополнительных условий в конечном решении.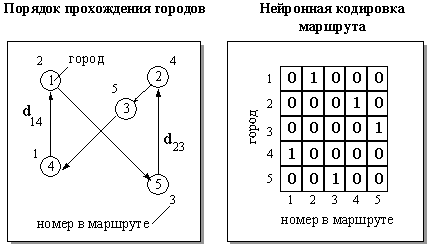
Рис. 6.1. Слева - один из возможных маршрутов коммивояжера в случае задачи с 5 городами. Справа - кодировка этого маршрута состояниями 25 бинарных нейронов
Осмысленному решению будет соответствовать стационарное состояние сети, в котором лишь  нейронов сети будут активными
(
нейронов сети будут активными
( 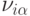 ) и в
каждом столбце и в каждой строке матрицы
) и в
каждом столбце и в каждой строке матрицы  будет находиться один и только один единичный элемент.
будет находиться один и только один единичный элемент.
Величина множителя Лагранжа  регулирует "торг" между поиском маршрута минимальной протяженности и осмысленностью вида
самого маршрута. Частное решение, соответствующее локальному минимуму функционала
регулирует "торг" между поиском маршрута минимальной протяженности и осмысленностью вида
самого маршрута. Частное решение, соответствующее локальному минимуму функционала 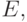 может быть осмысленным (второе слагаемое обращаются
на нем в ноль), но первое слагаемое (длина маршрута) для него, возможно будет слишком велико. Наоборот, длина маршрута может быть
достаточно мала, но одно из оставшихся слагаемых будет ненулевым и маршрут окажется не интерпретируем или недостаточен (например,
проходит не через все города).
может быть осмысленным (второе слагаемое обращаются
на нем в ноль), но первое слагаемое (длина маршрута) для него, возможно будет слишком велико. Наоборот, длина маршрута может быть
достаточно мала, но одно из оставшихся слагаемых будет ненулевым и маршрут окажется не интерпретируем или недостаточен (например,
проходит не через все города).
После того, как минимизируемая целевая функция для задачи коммивояжера построена, можно определить, какие связи в нейронной
сети Хопфилда следует выбрать, так чтобы функционал энергии состояния в ней совпал с этой функцией. Для этого достаточно приравнять
выражение для 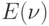 к энергии рекуррентной сети:
к энергии рекуррентной сети:

Таким образом находятся значения синаптических связей в сети:
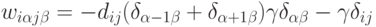
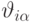 . Общее число весов в сети - порядка
. Общее число весов в сети - порядка 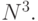
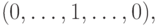 в котором единица помечает принимаемое
им значение. Если при решении задачи коммивояжера сопоставить таким нейронам города, а их состояния соотнести с номером города в туре,
то условие посещения города лишь однажды будет гарантировано автоматически.
в котором единица помечает принимаемое
им значение. Если при решении задачи коммивояжера сопоставить таким нейронам города, а их состояния соотнести с номером города в туре,
то условие посещения города лишь однажды будет гарантировано автоматически.После того как сеть построена, можно, стартуя со случайного начального состояния, проследить ее эволюцию к стационарной конфигурации, которая может дать если не оптимальное, то по крайней мере хорошее решение задачи. К сожалению, в описанном виде сеть чаще всего "застревает" в локальном минимуме относительно далеком от оптимума.
Для улучшения ситуации Хопфилд и Танк предложили использовать сети с непрерывными (аналоговыми) нейронами, принимающими любые
значения в интервале ![x_{i\alpha}\in [0,1]](/sites/default/files/tex_cache/c10f75634416c11a3f9e62b5eaf78d34.png) 2Состояния аналоговых нейронов мы обозначаем латинскими буквами, тогда как состояния бинарных нейронов - греческими.
В качестве тестовых они использовали задачи с 10 и 30 городами. В первом случае сеть в 20 попытках 16 раз
эволюционировала к состояниям, описывающим осмысленный маршрут и в 10 случаях давала один из двух возможных оптимальных маршрутов.
Поскольку для задачи с
2Состояния аналоговых нейронов мы обозначаем латинскими буквами, тогда как состояния бинарных нейронов - греческими.
В качестве тестовых они использовали задачи с 10 и 30 городами. В первом случае сеть в 20 попытках 16 раз
эволюционировала к состояниям, описывающим осмысленный маршрут и в 10 случаях давала один из двух возможных оптимальных маршрутов.
Поскольку для задачи с  городами полное число всевозможных маршрутов равно
городами полное число всевозможных маршрутов равно  !(делитель
!(делитель 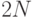 возникает вследствие инвариантности маршрута
относительно циклического сдвига и обращения направления движения), то в задаче с 10 городами оно составляет 181440. Таким образом,
выигрыш при использовании сети, по сравнению со случайным выбором составляет
возникает вследствие инвариантности маршрута
относительно циклического сдвига и обращения направления движения), то в задаче с 10 городами оно составляет 181440. Таким образом,
выигрыш при использовании сети, по сравнению со случайным выбором составляет  . В случае задачи с 30 городами полное число маршрутов
приблизительно равно
. В случае задачи с 30 городами полное число маршрутов
приблизительно равно  . Экономия, даваемая сетью, составила в этом случае
. Экономия, даваемая сетью, составила в этом случае  . В дальнейшем было показано, что использование
сети Кохонена дает лучшие результаты при решении той же задачи. Однако, поскольку на практике (в робототехнике, при проведении стыковки космических аппаратов, в автоматической навигации) необходимо быстро находить хорошее,
но не обязательно лучшее решение, то при электронной реализации аналоговая сеть Хопфилда дает исключительно эффективное решение задач
оптимизации.
. В дальнейшем было показано, что использование
сети Кохонена дает лучшие результаты при решении той же задачи. Однако, поскольку на практике (в робототехнике, при проведении стыковки космических аппаратов, в автоматической навигации) необходимо быстро находить хорошее,
но не обязательно лучшее решение, то при электронной реализации аналоговая сеть Хопфилда дает исключительно эффективное решение задач
оптимизации.
В дальнейшем разные исследователи выявили и другие особенности описанного подхода. Было показано, что недостатком оригинальной схемы Хопфилда и Танка является то, что простейшая сеть Хопфилда имеет тенденцию включать в маршрут ближайшие друг к другу города. Это происходит из-за того, что в определяющую длину маршрута часть функции Ляпунова входят парные произведения состояний нейронов сети. В результате, с увеличением числа городов маршрут, предлагаемый сетью, как правило, распадается на локально оптимальные участки, соединение которых, однако, далеко от оптимального. Ситуацию можно улучшить, если стимулировать сеть находить, например, локально наилучшие тройки городов. Для этого основная часть функции Ляпунова может быть представлена в виде
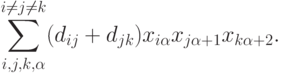
Однако, сети, динамика которых направляется такой функцией Ляпунова, должны состоять из более сложных нейронов, нелинейно суммирующих внешние воздействия - нейронов высокого порядка ( в данном случае - второго):
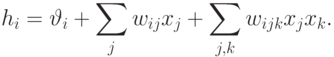
Купер показал, что использование таких сетей значительно улучшает результаты поиска оптимального решения. Так для  такая сеть
вдвое чаще находит оптимальное решение, чем обычная сеть Хопфилда. Повышение порядка сети приводит к дальнейшему улучшению
найденных сетью решений.
такая сеть
вдвое чаще находит оптимальное решение, чем обычная сеть Хопфилда. Повышение порядка сети приводит к дальнейшему улучшению
найденных сетью решений.
Отметим в заключение, что мы упомянули только о небольшой части разработанных к настоящему времени способов улучшения свойств минимизирующих энергию нейронных сетей при решения задач оптимизации.

