Алгоритмы архивации без потерь

Алгоритм декомпрессии, осуществляющий эту операцию, выглядит следующим образом:

code=File.ReadCode();
  while(code != СodeEndOfInformation){
    if(code = СlearСode) {
      InitTable();
      code=File.ReadCode();
      if(code = СodeEndOfInformation)
        {закончить работу};
        ImageFile.WriteString(StrFromTable(code));
      old_code=code;
    }
    else {
      if(InTable(code)) {
        ImageFile.WriteString(FromTable(code));
        AddStringToTable(StrFromTable(old_code)+
          FirstChar(StrFromTable(code)));
        old_code=code;
      }
      else {
        OutString= StrFromTable(old_code)+
          FirstChar(StrFromTable(old_code));
        ImageFile.WriteString(OutString);
        AddStringToTable(OutString);
        old_code=code;
      }
    }
  }

Здесь функция ReadCode() читает очередной код из декомпрессируемого файла. Функция InitTable() выполняет те же действия, что и при компрессии, т.е. очищает таблицу и заносит в нее все строки из одного символа. Функция FirstChar() выдает нам первый символ строки. Функция StrFromTable() выдает строку из таблицы по коду. Функция AddStringToTable() добавляет новую строку в таблицу (присваивая ей первый свободный код). Функция WriteString() записывает строку в файл.

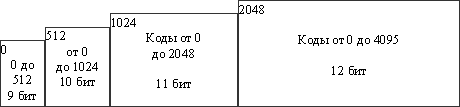
Замечание 1. Как вы могли заметить, записываемые в поток коды постепенно возрастают. До тех пор, пока в таблице не появится, например, в первый раз код 512, все коды будут меньше 512. Кроме того, при компрессии и при декомпрессии коды в таблице добавляются при обработке одного и того же символа, т.е. это происходит "синхронно". Мы можем воспользоваться этим свойством алгоритма для того, чтобы повысить степень компрессии. Пока в таблицу не добавлен 512 символ, мы будем писать в выходной битовый поток коды из 9 бит, а сразу при добавлении 512 - коды из 10 бит. Соответственно декомпрессор также должен будет воспринимать все коды входного потока 9-битными до момента добавления в таблицу кода 512, после чего будет воспринимать все входные коды как 10-битные. Аналогично мы будем поступать при добавлении в таблицу кодов 1024 и 2048. Данный прием позволяет примерно на 15% поднять степень компрессии (рис. 5.5):

Рис. 5.5.

Замечание 2. При сжатии изображения нам важно обеспечить быстроту поиска строк в таблице. Мы можем воспользоваться тем, что каждая следующая подстрока на один символ длиннее предыдущей, кроме того, предыдущая строка уже была нами найдена в таблице. Следовательно, достаточно создать список ссылок на строки, начинающиеся с данной подстроки, как весь процесс поиска в таблице сведется к поиску в строках, содержащихся в списке для предыдущей строки. Понятно, что такая операция может быть проведена очень быстро.

Заметим также, что реально нам достаточно хранить в таблице только пару <код предыдущей подстроки, добавленный символ>. Этой информации вполне достаточно для работы алгоритма. Таким образом, массив от 0 до 4095 с элементами <код предыдущей подстроки; добавленный символ; список ссылок на строки, начинающиеся с этой строки> решает поставленную задачу поиска, хотя и очень медленно.

На практике для хранения таблицы используется такое же быстрое, как в случае списков, но более компактное по памяти решение - хэш-таблица. Таблица состоит из 8192 (2¹³) элементов. Каждый элемент содержит <код предыдущей подстроки; добавленный символ; код этой строки>. Ключ для поиска длиной в 20 бит формируется с использованием двух первых элементов, хранимых в таблице как одно число ( key ). Младшие 12 бит этого числа отданы под код, а следующие 8 бит под значение символа.

В качестве хэш-функции при этом используется:

Index(key)= ((key >> 12) ^ key) & 8191;

Где >> - побитовый сдвиг вправо ( key >> 12 - мы получаем значение символа), ^ - логическая операция побитового исключающего ИЛИ, & логическое побитовое И.

Таким образом, за считанное количество сравнений мы получаем искомый код или сообщение, что такого кода в таблице нет.

Подсчитаем лучшую и худшую степень сжатия для данного алгоритма. Лучшее сжатие, очевидно, будет получено для цепочки одинаковых байт большой длины (т.е. для 8-битного изображения, все точки которого имеют, для определенности, цвет 0). При этом в 258 строку таблицы мы запишем строку "0, 0", в 259 - "0, 0, 0", ... в 4095 - строку из 3839 (=4095-256) нулей. При этом в поток попадет (проверьте по алгоритму!) 3840 кодов, включая код очистки. Следовательно, посчитав сумму арифметической прогрессии от 2 до 3839 (т.е. длину сжатой цепочки) и поделив ее на 3840*12/8 (в поток записываются 12-битные коды), мы получим лучшую степень сжатия.

Худшее сжатие будет получено, если мы ни разу не встретим подстроку, которая уже есть в таблице (в ней не должно встретиться ни одной одинаковой пары символов).

В случае, если мы постоянно будем встречать новую подстроку, мы запишем в выходной поток 3840 кодов, которым будет соответствовать строка из 3838 символов. Без учета замечания 1 это составит увеличение файла почти в 1.5 раза.

LZW реализован в форматах GIF и TIFF.