| Россия, г. Смоленск ул. Николаева д. 19а кв. 56 |
Методы контекстного моделирования
Пример 1
Рассмотрим процесс оценки отмеченного на рис 3.2 стрелкой символа 'л', встретившегося в блоке "молочное_молоко". Считаем, что модель работает на уровне символов.
Пусть мы используем контекстное моделирование порядка 2 и делаем полное смешивание оценок распределений вероятностей в КМ второго, первого и нулевого порядков с весами 0.6, 0.3 и 0.1. Считаем, что в начале кодирования в КМ(0) создаются счетчики для всех символов алфавита {'м', 'о', 'л', 'ч', 'н', 'е', '_', 'к'} и инициализируются единицей; счетчик символа после его обработки увеличивается на 1.
Для текущего символа 'л' имеются контексты "мо", "о" и пустой (нулевого порядка). К данному моменту для них накоплена статистика, показанная в табл. 3.1.
| Символы | 'м' | 'о' | 'л' | 'ч' | 'н' | 'е' | '_' | 'к' | |
|---|---|---|---|---|---|---|---|---|---|
| КМ порядка 0 (контекст "") | Частоты | 3 | 5 | 2 | 2 | 2 | 2 | 2 | 1 |
| Накопленные частоты | 3 | 8 | 10 | 12 | 14 | 16 | 18 | 19 | |
| КМ порядка 1 (контекст "о") | Частоты | - | - | 1 | 1 | - | 1 | - | - |
| Накопленные частоты | - | - | 1 | 2 | - | 3 | - | - | |
| КМ порядка 2("мо") | Частоты | - | - | 1 | - | - | - | - | - |
| Накопленные частоты | - | - | 1 | - | - | - | - | - |
Тогда оценка вероятности для символа 'л' будет равна
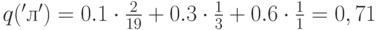
В общем случае, для однозначного кодирования символа 'л' такую оценку необходимо проделать для всех символов алфавита. Действительно, с одной стороны, декодер не знает, чему равен текущий символ, с другой стороны, оценка вероятности не гарантирует уникальность кода, а лишь задает его длину. Поэтому статистическое кодирование выполняется на основании накопленной частоты (см. подробности в примере 2 и в пункте "Арифметическое сжатие" главы 1). Например, если кодировать на основании статистики только нулевого порядка, то существует взаимно однозначное соответствие между накопленными частотами из диапазона (8,10] и символом 'л', что не имеет места в случае просто частоты (частоту 2 имеют еще 4 символа). Понятно, что аналогичные свойства остаются в силе и в случае оценок, получаемых частичным смешиванием.
Очевидно, что успех применения смешивания зависит от способа выбора весов w(o). Простой путь состоит в использовании заданного набора фиксированных весов КМ разных порядков при каждой оценке; этот способ был применен в примере 2. Естественно, альтернативой является адаптация весов по мере кодирования. Приспособление может заключаться в придании все большей значимости КМ все больших порядков или, скажем, попытке выбрать наилучшие веса на основании определенных статистических характеристик последнего обработанного блока данных. Но так исторически сложилось, что реальное развитие получили методы неявного взвешивания. Это объясняется в первую очередь их меньшей вычислительной сложностью.
Техника неявного взвешивания связана с введением вспомогательного символа ухода (escape). Символ ухода является квазисимволом и не должен принадлежать алфавиту сжимаемой последовательности. Фактически, он используется для передачи декодеру указаний кодера. Идея заключается в том, что если используемая КМ не позволяет оценить текущий символ (его счетчик равен 0 в этой КМ), то на выход посылается закодированный символ ухода и производится попытка оценить текущий символ в другой КМ, которой соответствует контекст иной длины. Обычно попытка оценки начинается с КМ наибольшего порядка N, затем в определенной последовательности осуществляется переход к контекстным моделям меньших порядков.
Естественно, статистическое кодирование символа ухода выполняется на основании его вероятности, так называемой вероятности ухода. Очевидно, что символы ухода порождаются не источником данных, а моделью. Следовательно, их вероятность может зависеть от характеристик сжимаемых данных, свойств КМ, с которой производится уход, свойств КМ, на которую происходит уход, и т.д. Как можно оценить эту вероятность, имея в виду, что конечный критерий качества - улучшение сжатия? Вероятность ухода - это вероятность появления в контексте нового символа. Тогда, фактически, необходимо оценить правдоподобность наступления ни разу не происходившего события. Теоретического фундамента для решения этой проблемы, видимо, не существует, но за время развития техник контекстного моделирования было предложено несколько подходов, хорошо работающих в большинстве реальных ситуаций. Кроме того, эксперименты показывают, что модели с неявным взвешиванием устойчивы относительно используемого метода оценки вероятности ухода, т.е. выбор какого-то способа вычисления этой величины не влияет на коэффициент сжатия кардинальным образом.

