|
Упражнение 2.1.25 |
Основные свойства контекстно-свободных языков
9.6. Пересечение контекстно-свободного языка с автоматным языком
Теорема 9.6.1. Если L1 - контекстно-свободный язык и L2 - автоматный язык, то язык 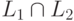 является контекстно-свободным.
является контекстно-свободным.
Доказательство.
Пусть  -
контекстно-свободная грамматика, порождающая язык L1.
Без ограничения общности можно считать, что множество P
содержит только правила вида
-
контекстно-свободная грамматика, порождающая язык L1.
Без ограничения общности можно считать, что множество P
содержит только правила вида 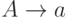 и
и  ,
где
,
где 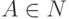 ,
, 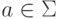 и
и  (см. теорему 8.3.3).
Пусть
(см. теорему 8.3.3).
Пусть  -
конечный автомат,
распознающий язык L_2.
Без ограничения общности можно считать, что
для каждого перехода
-
конечный автомат,
распознающий язык L_2.
Без ограничения общности можно считать, что
для каждого перехода  выполняется равенство |x| = 1
(см. лемму 2.3.3).
выполняется равенство |x| = 1
(см. лемму 2.3.3).
Построим контекстно-свободную грамматику 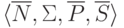 ,
порождающую язык
,
порождающую язык 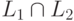 .
Положим
.
Положим
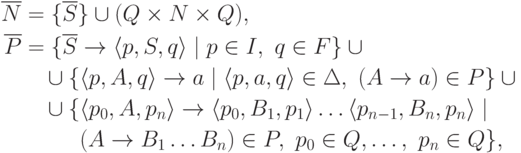
 -
новый символ (не принадлежащий множеству
-
новый символ (не принадлежащий множеству  ).
).Пример 9.6.2.
Пусть 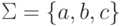 .
Рассмотрим
контекстно-свободный язык L1,
порождаемый грамматикой
.
Рассмотрим
контекстно-свободный язык L1,
порождаемый грамматикой

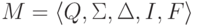 ,
где Q = {1,2}, I = {1}, F = {2},
,
где Q = {1,2}, I = {1}, F = {2},
![\objectwidth={5mm} \objectheight={5mm} \let\objectstyle=\scriptstyle
\xymatrix {
*=[o][F-]{1}
\ar @`{+/l16mm/} [] ^{}
\ar `ur_r{+/u7mm/}`r_dr{[0,2]}^{c} "1,3"
\ar "1,3" <0.6mm> ^{a}
&
& *=[o][F=]{2}
\ar "1,1" <0.6mm> ^{a}
\ar `dl_l{+/d7mm/}`l_ul{[0,-2]}^{b} "1,1"
}](/sites/default/files/tex_cache/da980c008f03074d7bfa4d3bbc37ac8c.png)
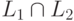 порождается контекстно-свободной грамматикой
порождается контекстно-свободной грамматикой
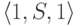 ,
,  ,
,  и
и  из доказательства теоремы 9.6.1.
из доказательства теоремы 9.6.1.Теорема 9.6.3*. Если L1 - линейный язык и L2 - автоматный язык, то язык 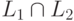 является линейным.
является линейным.
Пример 9.6.4*.
Пусть  .
Рассмотрим
линейный язык L1,
порождаемый грамматикой
.
Рассмотрим
линейный язык L1,
порождаемый грамматикой

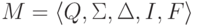 ,
где Q = {1,2,3}, I = {1}, F = {3},
,
где Q = {1,2,3}, I = {1}, F = {3},
![\objectwidth={5mm} \objectheight={5mm} \let\objectstyle=\scriptstyle
\xymatrix {
*=[o][F-]{1}
\ar @`{+/l16mm/} [] ^{}
\rloop{0,1} ^{a}
\rloop{0,-1} ^{b}
\ar "1,2" ^{a}
& *=[o][F-]{2}
\ar "1,3" ^{b}
& *=[o][F=]{3}
\rloop{0,1} ^{a}
\rloop{0,-1} ^{b}
}](/sites/default/files/tex_cache/e405d931a1c8f964bd956eb99355c5c8.png)
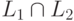 порождается контекстно-свободной грамматикой
порождается контекстно-свободной грамматикой
Упражнение 9.6.5. Найти контекстно-свободную грамматику для языка 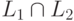 ,
где L1
порождается грамматикой
,
где L1
порождается грамматикой


Упражнение 9.6.6. Найти контекстно-свободную грамматику для языка 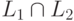 ,
где L1
порождается грамматикой
,
где L1
порождается грамматикой


Упражнение 9.6.7. Является ли контекстно-свободным язык 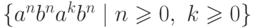
Упражнение 9.6.8. Является ли контекстно-свободным язык 
Упражнение 9.6.9.
Существует ли над алфавитом {a,b}
такой линейный
язык L,
что язык  не является контекстно-свободным?
не является контекстно-свободным?
