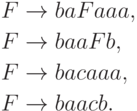|
Упражнение 2.1.25 |
Опубликован: 09.07.2007 | Уровень: профессионал | Доступ: платный | ВУЗ: Московский государственный университет имени М.В.Ломоносова
Лекция 10:
Основные свойства контекстно-свободных языков
9.3. Свойства замкнутости класса линейных языков
Пример 9.3.1.
Пусть 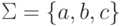 .
Язык
.
Язык  является линейным,
так как он порождается грамматикой
является линейным,
так как он порождается грамматикой

Пример 9.3.2.
Рассмотрим алфавит 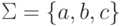 .
Язык
.
Язык


Теорема 9.3.3. Если L1 и L2 - линейные языки над алфавитом  , то
, то  тоже линейный язык.
тоже линейный язык.
Доказательство.
Пусть язык L1
порождается линейной грамматикой 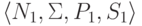 и L2
порождается линейной грамматикой
и L2
порождается линейной грамматикой  ,
где
,
где 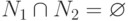 .
Тогда
.
Тогда  порождается грамматикой
порождается грамматикой
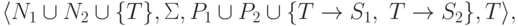
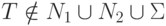 .
.Пример 9.3.4.
Рассмотрим алфавит 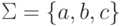 .
Язык
.
Язык
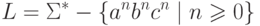


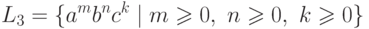
Упражнение 9.3.5.
Пусть 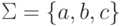 .
Является ли линейным язык
.
Является ли линейным язык  ?
?
Упражнение 9.3.6.
Пусть 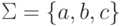 .
Является ли линейным язык
.
Является ли линейным язык  ?
?
Упражнение 9.3.7. Найти линейную грамматику, порождающую язык  ,
где L1
порождается грамматикой
,
где L1
порождается грамматикой