|
Упражнение 2.1.25 |
Слова, языки и грамматики
1.3. Гомоморфизмы
Определение 1.3.1. Пусть 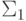 и
и  - алфавиты.
Если отображение
- алфавиты.
Если отображение  удовлетворяет условию
удовлетворяет условию 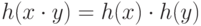 для всех слов
для всех слов 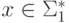 и
и 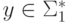 ,
то отображение h
называется гомоморфизмом
( морфизмом ).
,
то отображение h
называется гомоморфизмом
( морфизмом ).
Замечание 1.3.2.
Можно доказать, что если  - гомоморфизм,
то
- гомоморфизм,
то 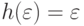 .
.
Замечание 1.3.3. Пусть 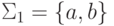 и
и 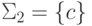 .
Тогда отображение
.
Тогда отображение  ,
заданное равенством
,
заданное равенством  ,
является гомоморфизмом.
,
является гомоморфизмом.
Замечание 1.3.4. Каждый гомоморфизм однозначно определяется своими значениями на однобуквенных словах.
Замечание 1.3.5.
Если  -
гомоморфизм и
-
гомоморфизм и 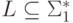 ,
то через h(L)
обозначается язык
,
то через h(L)
обозначается язык 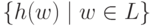 .
.
Пример 1.3.6.
Пусть  и гомоморфизм
и гомоморфизм 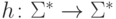 задан равенствами h(a) = abba
и
задан равенствами h(a) = abba
и 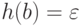 .
Тогда
.
Тогда
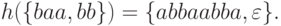
Определение 1.3.7. Если  -
гомоморфизм и
-
гомоморфизм и 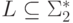 ,
то через h-1(L)
обозначается язык
,
то через h-1(L)
обозначается язык 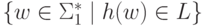 .
.
Пример 1.3.8. Рассмотрим алфавит  .
Пусть гомоморфизм
.
Пусть гомоморфизм 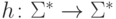 задан равенствами h(a) = ab
и h(b) = abb.
Тогда
задан равенствами h(a) = ab
и h(b) = abb.
Тогда

Упражнение 1.3.9. Пусть 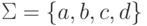 .
Существует ли такой гомоморфизм
.
Существует ли такой гомоморфизм 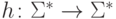 ,
что h(abc) = bac
и h(da) = ba?
,
что h(abc) = bac
и h(da) = ba?
Упражнение 1.3.10.
Существуют ли такой язык  и такой гомоморфизм
и такой гомоморфизм 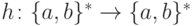 ,
что
,
что 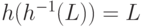 и
и 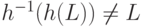 ?
?
Упражнение 1.3.11. Пусть  .
Существует ли
такой гомоморфизм
.
Существует ли
такой гомоморфизм 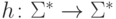 ,
что
,
что  и
и  ?
?
Упражнение 1.3.12. Существуют ли такой язык  и такой гомоморфизм
и такой гомоморфизм 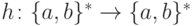 ,
что
,
что  и
и 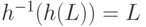 ?
?
Упражнение 1.3.13. Пусть 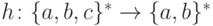 -
гомоморфизм, заданный соотношениями h(a) = a, h(b) = ba, h(c) = bb.
Существуют ли такие слова u и v,
что |u|<|v|
и |h(u)|>|h(v)|?
-
гомоморфизм, заданный соотношениями h(a) = a, h(b) = ba, h(c) = bb.
Существуют ли такие слова u и v,
что |u|<|v|
и |h(u)|>|h(v)|?
