Минимизация неполностью определенных функций
Операция штрих Шеффера
Заметим, что эта функция дуальна по отношению к f8, поэтому все свойства являются по существу дуально вытекающими из рассмотренных.
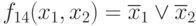 (запись функций по нулям)
(запись функций по нулям)
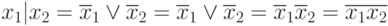
на основе принципа суперпозиции:
x1 | x2 | . . . | xn = x1x2...xn
Рассмотрим некоторые эквивалентности:
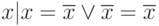
x1 | x2 | x3 = (x1 x2)| x3 = x1| (x2 x3)
x1 | x2 | x3| x4 = (x1 x2)| (x3 x4)
Сформулируем правила перехода от ДНФ функции к выражению с использованием операции " Штрих Шеффера ".
- заменить все операции дизъюнкции на операции Шеффера
- заменить все операции конъюнкции на операции Шеффера
- группы букв, которые соответствуют дизъюнктивным членам, заключить в скобки.
Пример:
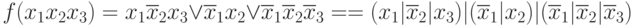
То же самое можно утверждать относительно минимальной формы.
В заключение необходимо отметить, что в настоящее время вопросы синтеза функций в одноэлементном базисе приобретают большое значение, так как соответствующие элементы используют операцию Пирса и Шеффера. Однако в полной мере теоретически методы синтеза разработаны не столь детально, как это сделано в базисе "и", "или", "инверсия".
Минимальные конъюнктивные нормальные формы
Как было отмечено, для получения минимальной формы функции нужно построить как МДНФ так и МКНФ.
Рассмотрим построение МКНФ.
В основном методы получения МКНФ аналогичны методам получения МДНФ и поэтому сформулируем лишь правила получения МКНФ:
- Представить ФАЛ в СКНФ. Если она задана таблицей, то произвести запись функции по нулям, как это было сформулировано ранее. Если дана СДНФ, то из нее легко получить СКНФ:
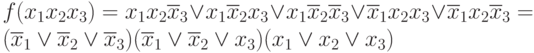 ,
,т.е. нужно функцию представить в виде конъюнкции недостающего числа дизъюктивных членов с соответсвенно расставлеными отрицаниями.
- При задании функции в произвольной конъюктивной форме, применяя
формулы развертывания:
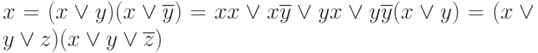
. . . . . . . . . . . .,
- Выполнить все операции неполного склеивания:
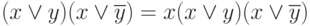
- Применить любой из методов минимизации: испытание членов, диаграммы Вейча, метод импликантных матриц.
- При выполнении метода испытания членов необходимо каждый конъюктивный член приравнять нулю. Найти значения аргументов, которые обращают его в нуль, удалить его из выражения функции и найти значение функции при найденных значениях аргументов. Если функция обратится в нуль, то конъюктивный член является лишним.
По возможности отбросить одновременно несколько членов, поступить как и при минимизации функции ДНФ.
- При использовании диаграмм Вейча ищутся правильные конфигурации, образованные нулями.
- При применении метода импликантных матриц поступают как и в случае ДНФ, только колонкам присваивают имена конституент " 0 " функции, записанной в СКНФ, а горизонтальным рядам – простых импликант. Далее ищут оптимальное покрытие.
- При выполнении метода испытания членов необходимо каждый конъюктивный член приравнять нулю. Найти значения аргументов, которые обращают его в нуль, удалить его из выражения функции и найти значение функции при найденных значениях аргументов. Если функция обратится в нуль, то конъюктивный член является лишним.

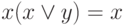 , получить сокращенную
, получить сокращенную