Логические и арифметические основы и принципы работы ЭВМ

:

Логические и арифметические основы и принципы работы ЭВМ
[+]
Опубликован: 30.03.2005 | Уровень: специалист | Доступ: платный | ВУЗ: Национальный исследовательский ядерный университет «МИФИ»
Лекция 5:

Минимизация неполностью определенных функций
A
|
версия для печати
< Лекция 4 || Лекция 5: 123 || Лекция 6 >

Синтез переключательных функций в одноэлементном базисе

Операция (стрелка) Пирса

f8(x1,x2)
x1 0 0 1 1
x2 0 1 0 1
f8 1 0 0 0

Эту функцию можем представить, записав по "единицам":

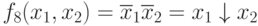
f_{8}(x_{1},x_{2}) = \overline{x}_{1}\overline{x}_{2} = x_{1}\downarrow x_{2}

или

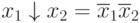
x_{1}\downarrow x_{2} = \overline{x}_{1}\overline{x}_{2}

На основе принципа суперпозиции:

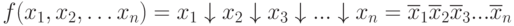
f(x_{1},x_{2},\dots x_{n}) = x_{1}\downarrow x_{2}\downarrow x_{3}\downarrow . . . \downarrow x_{n} = \overline{x}_{1}\overline{x}_{2}\overline{x}_{3} . . .\overline{x}_{n}

Применяя правило де Моргана:

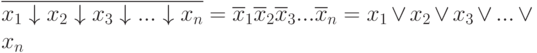
\overline{x_{1}\downarrow x_{2}\downarrow x_{3}\downarrow . . .\downarrow x_{n}} = \overline{x}_{1}\overline{x}_{2}\overline{x}_{3} . . .\overline{x}_{n} = x_{1} \vee x_{2} \vee x_{3} \vee . . .\vee x_{n}

или:

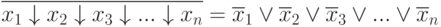
\overline{x_{1}\downarrow x_{2}\downarrow x_{3}\downarrow . . .\downarrow x_{n}} = \overline{x}_{1} \vee \overline{x}_{2} \vee \overline{x}_{3} \vee . . .\vee \overline{x}_{n}

т.е.

x_{1}\downarrow x_{2}\downarrow x_{3}\downarrow . . .\downarrow x_{n} = \overline{x_{1} \vee x_{2} \vee x_{3} \vee . . . \vee x_{n}}

Рассмотрим некоторые соотношения для операции Пирса:

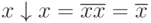
x\downarrow x = \overline{x}\overline{x} = \overline{x}

x_{1}\downarrow x_{2} = \overline{x}_{1}\overline{x}_{2} = \overline{x}_{2}\overline{x}_{1} = x_{2}\downarrow x_{1}

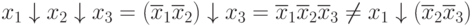x_{1}\downarrow x_{2}\downarrow x_{3} = (\overline{x}_{1}\overline{x}_{2})\downarrow x_{3} = \overline{x}_{1}\overline{x}_{2}\overline{x}_{3} \ne x_{1}\downarrow (\overline{x}_{2}\overline{x}_{3}),

т.е. операция Пирса не обладает свойством ассоциативности

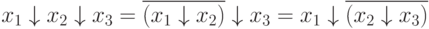
x_{1}\downarrow x_{2}\downarrow x_{3} = \overline{(x_{1}\downarrow x_{2})}\downarrow x_{3} = x_{1}\downarrow \overline{(x_{2}\downarrow x_{3})}

x_{1}\downarrow x_{2}\downarrow x_{3}\downarrow x_{4} = \overline{(x_{1}\downarrow x_{2})}\downarrow \overline{(x_{3}\downarrow x_{4})}

При этом порядок выполнения операций в формулах, где есть операции Пирса такой:

  1. раскрываются скобки
  2. выполняются операции инверсии
  3. выполняются операции Пирса

Синтез логических функций в базисе Пирса удобно производить, имея запись функции в КНФ.

Допустим, что ФАЛ задана в конъюктивной форме

f = Q1Q2Q3 . . . Qn

Подставим член Qi в виде:

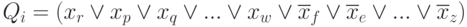
Q_{i} = (x_{r} \vee x_{p} \vee x_{q} \vee . . . \vee x_{w} \vee \overline{x}_{f} \vee \overline{x}_{e} \vee . . . \vee \overline{x}_{z})

Возьмем двойное отрицание от обеих частей этого равенства, применив правило де Моргана

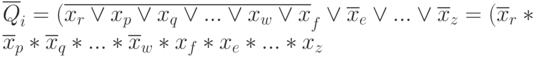
\overline{Q}_{i} = (\overline{x_{r} \vee x_{p} \vee x_{q} \vee . . . \vee x_{w} \vee x}_{f} \vee \overline{x}_{e} \vee . . . \vee \overline{x}_{z} = (\overline{x}_{r} * \overline{x}_{p} * \overline{x}_{q} * . . . * \overline{x}_{w} * x_{f} * x_{e} * . . . * x_{z}

Применяя соотношение, полученное на основе принципа суперпозиции:

Q_{i} = (\overline{x_{r}\downarrow x_{p}\downarrow x_{q}\downarrow . . .\downarrow x_{w}\downarrow x}_{f}\downarrow \overline{x}_{e}\downarrow . . .\downarrow \overline{x}_{z}

Или, применяя это преобразование к исходной форме, получим:

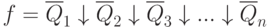
f = \overline{Q}_{1}\downarrow \overline{Q}_{2}\downarrow \overline{Q}_{3}\downarrow . . .\downarrow \overline{Q}_{n}

Итак: чтобы от КНФ перейти к базису Пирса и инверсии необходимо:

  1. заменить операции дизъюнкции операциями Пирса
  2. заменить операции конъюнкции операциями Пирса
  3. заключить в скобки все те группы букв, которые соответсвуют конъюнктивным членам.

Пример:

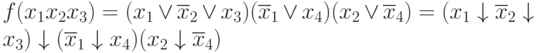
f(x_{1}x_{2} x_{3}) = (x_{1} \vee \overline{x}_{2} \vee x_{3}) (\overline{x}_{1} \vee x_{4}) (x_{2} \vee \overline{x}_{4}) = (x_{1}\downarrow \overline{x}_{2}\downarrow x_{3})\downarrow (\overline{x}_{1}\downarrow x_{4}) (x_{2}\downarrow \overline{x}_{4})

Замечание. Так как в этих произведениях число букв не увеличивается, и если исходная форма функции была минимальной, то вновь полученная также будет минимальной (в действительности дело обстоит сложнее, поскольку мы рассматриваем не базис " 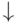\downarrow ", а другой, то есть " 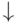\downarrow " и " - " - операцию Пирса и инверсию).

Принципиально можно избавиться от отрицаний, применив соотношение: 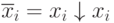\overline{x}_{i} = x_{i}\downarrow x_{i}, но тогда нельзя будет утверждать, что полученная форма будет минимальной!

Дальше >>
< Лекция 4 || Лекция 5: 123 || Лекция 6 >

Вопросы и ответы

вопросов: 6
Жаксылык Несипов
Жаксылык Несипов
ответить
Людмила Долгих
Людмила Долгих

Здравствуйте. В первой лекции курса "Логические и арифметические основы и принципы работы ЭВМ" у вас приведена классическая структурная схема ЭВМ. Если можно уточните, а как в классической архитектуре могла реализоваться прямая работа устройств ввода-вывода с оперативной памятью?  Если я правильно понимаю - это режим прямого доступа к памяти, в классической архитектуре он не предусмотрен.

ответить

Студенты

всего: 82 | онлайн: 1
Дмитрий Жилин
Дмитрий Жилин
Россия, Ул. Автостроителей 6
предложить дружбу