НОУ ИНТУИТ | Компьютерное моделирование. Лекция 3: Типовые математические модели

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 16.11.2010 | Уровень: специалист | Доступ: платный

|

Вам нравится? Нравится 50 студентам

| Поделиться |

Поддержать программу

2.4. Элементы СМО, краткая характеристика

При решении задач управления, в том числе и управления войсками, часто возникает ряд однотипных задач:

оценка пропускной способности направления связи, железнодорожного узла, госпиталя и т. п.;
оценка эффективности ремонтной базы;
определение количества частот для радиосети и др.

Все эти задачи однотипны в том смысле, что в них присутствует массовый спрос на обслуживание. В удовлетворении этого спроса участвует определенная совокупность элементов, образующая систему массового обслуживания (СМО) (рис. 2.9).

увеличить изображение
Рис. 2.9. Система массового обслуживания

Элементами СМО являются:

входной (входящий) поток требований (заявок) на обслуживание;
приборы (каналы) обслуживания;
очередь заявок, ожидающих обслуживания;
выходной (выходящий) поток обслуженных заявок;
поток не обслуженных заявок;
очередь свободных каналов (для многоканальных СМО).

Входящий поток - это совокупность заявок на обслуживание. Часто заявка отождествляется с ее носителем. Например, поток неисправной радиоаппаратуры, поступающий в мастерскую объединения, представляет собой поток заявок - требований на обслуживание в данной СМО.

Как правило, на практике имеют дело с так называемыми рекуррентными потоками, - потоками, обладающими свойствами:

стационарности;
ординарности;
ограниченного последействия.

Первые два свойства мы определили ранее. Что касается ограниченного последействия, то оно заключается в том, что интервалы между поступающими заявками являются независимыми случайными величинами.

Рекуррентных потоков много. Каждый закон распределения интервалов порождает свой рекуррентный поток. Рекуррентные потоки иначе называют потоками Пальма.

Поток с полным отсутствием последействия, как уже отмечалось, называется стационарным пуассоновским. У него случайные интервалы между заявками имеют экспоненциальное распределение:

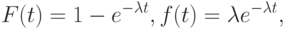
$F(t) = 1 - e^{ - \lambda t}, f(t) = \lambda e^{ - \lambda t},$

здесь $\lambda$ - интенсивность потока.

Название потока - пуассоновский - происходит от того, что для этого потока вероятность 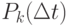$P_{k} (\Delta t)$ появления заявок за интервал $\Delta t$ определяется законом Пуассона:

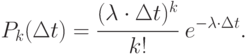
$P_k(\Delta t) = \cfrac{(\lambda\cdot\Delta{t})^k}{k!}\;e^{ - \lambda \cdot\Delta{t}}.$

Поток такого типа, как отмечалось ранее, называют также простейшим. Именно такой поток предполагают проектировщики при разработке СМО. Вызвано это тремя причинами.

Во-первых,поток этого типа в теории массового обслуживания аналогичен нормальному закону распределения в теории вероятностей в том смысле, что к простейшему потоку приводит предельный переход для потока, являющегося суммой потоков с произвольными характеристиками при бесконечном увеличении слагаемых и уменьшении их интенсивности. То есть сумма произвольных независимых (без преобладания) потоков с интенсивностями 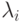$\lambda_{i}$ является простейшим потоком с интенсивностью

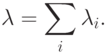
$\lambda = \sum_{i}\lambda_{i}.$

Во-вторых, если обслуживающие каналы (приборы) рассчитаны на простейший поток заявок, то обслуживание других типов потоков (с той же интенсивностью) будет обеспечено с не меньшей эффективностью.

В-третьих, именно такой поток определяет марковский процесс в системе и, следовательно, простоту аналитического анализа системы. При других потоках анализ функционирования СМО сложен.

Часто встречаются системы, у которых поток входных заявок зависит от количества заявок, находящихся в обслуживании. Такие СМО называют замкнутыми (иначе - разомкнутыми). Например, работа мастерской связи объединения может быть представлена моделью замкнутой СМО. Пусть эта мастерская предназначена для обслуживания радиостанций, которых в объединении . Каждая из них имеет интенсивность отказов $\lambda$ . Входной поток отказавшей аппаратуры будет иметь интенсивность $\lambda_{р}$ :

$\lambda_{р} = \lambda(m-n),$

где - количество радиостанций, уже находящихся в мастерской на ремонте.

Заявки могут иметь разные права на начало обслуживания. В этом случае говорят, что заявки неоднородные. Преимущества одних потоков заявок перед другими задаются шкалой приоритетов.

Важной характеристикой входного потока является коэффициент вариации:

$\nu = \cfrac{\sigma}{\overline{\tau}_{инт}},$

где $\overline{\tau}_{инт}$ - математическое ожидание длины интервала;

$\sigma$ - среднеквадратическое отклонение случайной величины (длины интервала) $\tau_{инт}$ .

Для простейшего потока 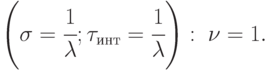$\left( {\sigma = \cfrac{1}{\lambda };{\tau _{инт}} = \cfrac{1}{\lambda }} \right):\;\nu = 1.$

Для большинства реальных потоков $0 \le \nu \le 1$ .

При $\nu = 0$ поток регулярный, детерминированный.

Коэффициент вариации - характеристика, отражающая степень неравномерности поступления заявок.

Каналы (приборы) обслуживания. В СМО могут быть один или несколько обслуживающих приборов (каналов). Согласно с этим СМО называют одноканальными или многоканальными.

Многоканальные СМО могут состоять из однотипных или разнотипных приборов. Обслуживающими приборами могут быть:

линии связи;
мастера ремонтных органов;
взлетно-посадочные полосы;
транспортные средства;
причалы;
парикмахеры, продавцы и др.

Основная характеристика канала - время обслуживания. Как правило, время обслуживания - величина случайная.

Обычно практики полагают, что время обслуживания имеет экспоненциальный закон распределения:

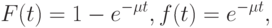
$F(t) = 1-e^{-\mu t}, f(t) = \mue e^{-\mu t},$

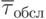где $\mu$ - интенсивность обслуживания, $\mu = \cfrac{1}{\overline{\tau}_{обсл}}$ ;

${\overline{\tau}_{обсл}}$ - математическое ожидание времени обслуживания.

То есть процесс обслуживания - марковский, а это, как теперь нам известно, дает существенные удобства в аналитическом математическом моделировании.

Кроме экспоненциального встречаются -распределение Эрланга, гиперэкспоненциальное, треугольное и некоторые другие. Это нас не должно смущать, так как показано, что значение критериев эффективности СМО мало зависят от вида закона распределения вероятностей времени обслуживания.

При исследовании СМО выпадает из рассмотрения сущность обслуживания, качество обслуживания.

Каналы могут быть абсолютно надежными, то есть не выходить из строя. Вернее, так может быть принято при исследовании. Каналы могут обладать конечной надежностью. В этом случае модель СМО значительно сложнее.

Очередь заявок. В силу случайного характера потоков заявок и обслуживания пришедшая заявка может застать канал (каналы) занятым обслуживанием предыдущей заявки. В этом случае она либо покинет СМО не обслуженной, либо останется в системе, ожидая начало своего обслуживания. В соответствии с этим различают:

СМО с отказами;
СМО с ожиданием.

СМО с ожиданием характеризуются наличием очередей. Очередь может иметь ограниченную или неограниченную емкость: 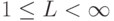$1 \le L < \infty$ .

Исследователя обычно интересуют такие статистические характеристики, связанные с пребыванием заявок в очереди:

среднее количество заявок в очереди за интервал исследования;
среднее время пребывания (ожидания) заявки в очереди. СМО с ограниченной емкостью очереди относят к СМО смешанного типа.

Нередко встречаются СМО, в которых заявки имеют ограниченное время пребывания в очереди независимо от ее емкости. Такие СМО также относят к СМО смешанного типа.

Выходящий поток - это поток обслуженных заявок, покидающих СМО.

Встречаются случаи, когда заявки проходят через несколько СМО: транзитная связь, производственный конвейер и т. п. В этом случае выходящий поток является входящим для следующей СМО. Совокупность последовательно связанных между собой СМО называют многофазными СМО или сетями СМО.

Входящий поток первой СМО, пройдя через последующие СМО, искажается и это затрудняет моделирование. Однако следует иметь в виду, что при простейшем входном потоке и экспоненциальном обслуживании (то есть в марковских системах) выходной поток тоже простейший. Если время обслуживания имеет не экспоненциальное распределение, то выходящий поток не только не простейший, но и не рекуррентный.

Заметим, что интервалы между заявками выходящего потока, это не то же самое, что интервалы обслуживания. Ведь может оказаться, что после окончания очередного обслуживания СМО какое-то время простаивает из-за отсутствия заявок. В этом случае интервал выходящего потока состоит из времени незанятости СМО и интервала обслуживания первой, пришедшей после простоя, заявки.

В системах с отказами есть поток необслуженных заявок. Если в СМО с отказами поступает рекуррентный поток, а обслуживание - экспоненциальное, то и поток необслуженных заявок - рекуррентный.

Очереди свободных каналов. В многоканальных СМО могут образовываться очереди свободных каналов. Количество свободных каналов - величина случайная. Исследователя могут интересовать различные характеристики этой случайной величины. Обычно это среднее число каналов, занятых обслуживанием за интервал исследования.

Таким образом, по признакам, влияющим на функционирование, СМО может принадлежать к одному из типов в соответствии с приводимой классификацией (рис. 2.10).

Рис. 2.10. Классификация СМО

Для обозначения простых (однофазных) СМО используется символика, предложенная Кендаллом:

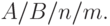
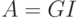- входящий поток заявок: A = GI - рекуррентный поток; A = М - простейший поток с показательным законом распределения вероятностей; A = D - регулярный или детерминированный поток (с постоянными интервалами между моментами поступления заявок).

- случайная длительность обслуживания: B = G или B = GI - рекуррентное обслуживание с одной и той же функцией распределения B(t) для разных каналов; B = М - показательное обслуживание; B = D - регулярное обслуживание.

- количество обслуживающих каналов. Если $n > 1$ , то система называется многоканальной.

- количество мест для ожидания заявок в очереди. Если m = 0 , то СМО с потерями (без ожидания); $m = \infty$ - система с неограниченным ожиданием; $0 < m < \infty$ - система с ограниченным числом мест для ожидания.