| Россия |
Калейдоскоп из комбинаторных алгоритмов
Программа 9. Сортировка строк матрицы.
//Cортировка строк матрицы. В каждой строке подсчитывается сумма
//простых чисел. Полученный вектор упорядочивается по возрастанию.
//Строки матрицы переставляются по новому вектору.
//Алгоритм реализован на Turbo C++.
#include<stdio.h>
#include<conio.h>
#define n 5
struct summa
{
int value;
int idx;
} sum,massum[n],a;
void main(void){
clrscr();
int mas1[n][n],mas[n][n]={{1,1,1,1,1},
{3,16,11,6,4},
{8,10,15,23,1},
{3,8,10,15,3},
{7,3,20,15,10}};
int i,j,k,flag;
for(i=0;i<n;i++){
sum.value=0;
for(j=0;j<n;j++){
flag=0;
if(mas[i][j]>2)
for(k=2;k<mas[i][j];k++)
if(mas[i][j]%k==0) flag=1;
if(flag==0) sum.value=sum.value+mas[i][j];
}
sum.idx=i;
massum[i]=sum;
}
for(i=0;i<n-1;i++)
for(j=0;j<n-1-i;j++){
if (massum[j].value>massum[j+1].value){
a=massum[j];
massum[j]=massum[j+1];
massum[j+1]=a;
}
}
for(i=0;i<n;i++)
for(j=0;j<n;j++)
mas1[i][j]=mas[massum[i].idx][j];
for(i=0;i<n;i++){
for(j=0;j<n;j++)
printf("%3d ",mas[i][j]);
printf("\n");
}
printf("\n\n\n");
for(i=0;i<n;i++){
for(j=0;j<n;j++)
printf("%3d ",mas1[i][j]);
printf("\n");
}
getch();
}Задача о назначениях (задачи выбора)
Эта задача состоит в следующем. Пусть имеется  работ и
работ и  кандидатов для
выполнения этих работ. Назначение кандидата
кандидатов для
выполнения этих работ. Назначение кандидата  на работу
на работу  связано с затратами
связано с затратами 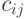
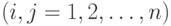 . Требуется найти
назначение кандидатов на все работы, дающее
минимальные суммарные затраты; при этом каждого кандидата можно назначить
только на одну работу и каждая работа может быть занята только одним
кандидатом.
. Требуется найти
назначение кандидатов на все работы, дающее
минимальные суммарные затраты; при этом каждого кандидата можно назначить
только на одну работу и каждая работа может быть занята только одним
кандидатом.
Иначе говоря, решение этой задачи представляет собой перестановку
( 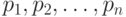 ) чисел
) чисел  ; каждое
из производимых
назначений описывается соответствием
; каждое
из производимых
назначений описывается соответствием  (
( 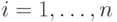 ).
Указанные условия единственности при этом автоматически выполняются, и
нашей целью является минимизация суммы
).
Указанные условия единственности при этом автоматически выполняются, и
нашей целью является минимизация суммы
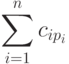 |
( 17.1) |
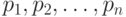 ).
).Перед нами типичная экстремальная комбинаторная задача. Ее решение путем
прямого перебора, то есть вычисления значений функции 17.1 на всех
перестановках и сравнения, практически невозможно при сколько-нибудь
больших  , поскольку число перестановок равно
, поскольку число перестановок равно 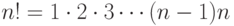 . Попытаемся свести дело к линейному программированию.
. Попытаемся свести дело к линейному программированию.
Конечное множество, на котором задана целевая функция 17.1, представляет
собой множество всех перестановок чисел  . Как
известно, каждая такая перестановка может быть описана точкой в
. Как
известно, каждая такая перестановка может быть описана точкой в 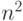 -мерном евклидовом
пространстве; эту точку удобнее всего представить в виде
-мерном евклидовом
пространстве; эту точку удобнее всего представить в виде  -матрицы
-матрицы 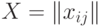 . Элементы
. Элементы 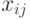 интерпретировать следующим образом:
интерпретировать следующим образом:
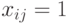 , если i-й кандидат назначается на j-ю работу,
, если i-й кандидат назначается на j-ю работу,
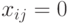 , в противном случае.
, в противном случае.
Элементы матрицы должны быть подчинены двум условиям:
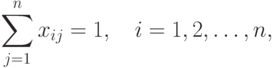 |
( 17.3) |
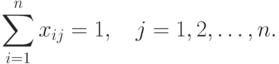 |
( 17.4) |
 имеется ровно по одной единице. Говоря
неформально, условие 17.3 означает, что каждый кандидат может быть назначен только на
одну работу, а условие 17.4 — что каждая работа предназначена только для
одного кандидата. (Матрицу перестановок можно получить из единичной
матрицы путем некоторой перестановки ее строк.)
имеется ровно по одной единице. Говоря
неформально, условие 17.3 означает, что каждый кандидат может быть назначен только на
одну работу, а условие 17.4 — что каждая работа предназначена только для
одного кандидата. (Матрицу перестановок можно получить из единичной
матрицы путем некоторой перестановки ее строк.)Теперь задача заключается в нахождении чисел 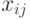 ,
удовлетворяющих условиям
17.2, 17.3, 17.4 и минимизирующих суммарные затраты 17.1, которые теперь можно
переписать в виде
,
удовлетворяющих условиям
17.2, 17.3, 17.4 и минимизирующих суммарные затраты 17.1, которые теперь можно
переписать в виде
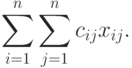 |
( 17.5) |
 |
( 17.6) |
Программа 10.Назначение на работу.
program one;{Назначение на работу.
Рассматривается случай: 10 работ и 10 желающих.
реализовано на Turbo-Pascal}
uses crt;
const n=10;
var C : array [1..n,1..n] of integer;
T : array [1..n] of integer;
M : array [1..n,1..4] of integer;
Sum,tmj,z,min,i,j,tmp:integer;
begin
clrscr;
randomize;
write('work - ');
for i:=1 to n do write(i:2,' ');
for i:=1 to n do begin
writeln;
write(i:2,' man ');
for j:=1 to n do begin
C[i,j]:=random(100);
{if M[i,j]>max then max:=M[i,j];}
{if C[i,j]<min then begin M[1]:=C[i,j]; M[2]:=i; M[3]:=j; end; }
write(C[i,j]:2,' ');
end;
end;
writeln;
for j:=1 to n do T[j]:=0;
Sum:=0;
for i:=1 to n do begin
writeln;
write(i:2,' man ');
min:=100;
for j:=1 to n do begin
if (C[i,j]<min) and (T[j]=0) then begin min:=C[i,j]; M[i,1]:=i;
M[i,2]:=j; M[i,3]:=C[i,j]; tmj:=j;
end;
write(C[i,j]:2,' ');
end;
T[tmj]:=1;
{M[i,3]:=min;}
Sum:=Sum+M[i,3];
write('=',M[i,3]:2,' man=',M[i,1],' job=',M[i,2]);
end;
writeln;
{for i:=1 to n do begin
for j:=1 to n do begin
if (i<>j) and (M[i,2]=M[j,2]) then begin
M[j,3]:=C[j,1];
for z:=1 to n do begin
if (M[j,3]>C[j,z]) and (z<>M[j,2]) then begin M[j,3]:=C[j,z];
M[j,2]:=z; end;
end;
end;
end;
writeln('=',M[i,3]:2,' man=',M[i,1],' job=',M[i,2]);
end;
}
write('sum=',Sum);
readln;
end.Программа 11.Назначение на работу.
/*
Назначение на работу.
Рассматривается случай: 6 работ и 6 желающих.
*/
//Назначение на работу. Реализовано на Turbo C++.
#include <stdio.h>
#include <iostream.h>
#include <stdlib.h>
#include <conio.h>
#define k 6
int Sum,tmj,i,j,zj,min,tmp,min2,tmj2,p,q,ki;
int M[k][4], C[k][k], T[k][2], Temper[k][2];
char a;
/*struct myst
{int cel;
float rac;
};
myst ctpyk[k];*/
main()
{
Sum=0;
min=100;
for(i=1;i<k;i++)
{ T[i][1]=0;
printf("\n");
for(j=1;j<k;j++)
{C[i][j]=rand()/1000 +1;
// printf(" %d ", C[i][j]);
}
}
for(i=1;i<k;i++)
{
min=100;
printf("\n");
for(j=1;j<k;j++)
{
if(C[i][j]<min/* && T[j][1]==0*/)
{
if(T[j][1]==0)
{
min=C[i][j]; //m[i][1] - 4el, m[i][2] -job, m[i][3]
- stoimost.
M[i][1]=i;
M[i][2]=j;
M[i][3]=C[i][j];
tmj=j;
}
/* else
{
if(C[i][j]<C[T[j][2]][j])
{
ki=T[j][2];
T[j][2]=0;
// T[j][1]=0;
min=C[i][j];
M[i][1]=i;
M[i][2]=j;
M[i][3]=C[i][j];
tmj=j;
for(zj=1;zj<k;zj++)
{
min2=100;
if(C[ki][zj]<min2 && zj!=tmj &&
T[zj][1]==0)
{
min2=C[ki][zj];
tmj2=zj;
M[ki][1]=ki;
M[ki][2]=zj;
M[ki][3]=C[ki][zj];
}
}
T[tmj2][2]=ki;
T[tmj2][1]=min2;
}
*/
}
printf(" %d ", C[i][j]);
}
T[tmj][2]=i;
T[tmj][1]=min;
//na4alo mega funkcii
/* if(C[i][j]<min && T[j][1]!=0)
{
for(p=1;pk;p++)
{
if(C[T[tmj][2]][p]
}
}
*/
//konec.
Sum=Sum+M[i][3];
printf(" $= %d, man= %d, job= %d ",M[i][3],M[i][1],M[i][2]);
}
/* for(i=0;i<k;i++)
{ctpyk[i].cel=rand();
ctpyk[i].rac=rand()/1000;
printf("%d %f \n", ctpyk[i].cel, ctpyk[i].rac);}
*/
scanf("%d",a);
return 0;
}
