Действия над степенными рядами
Перейдем теперь к действиям над степенными рядами. Пусть функции  и
и 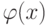 разложены в степенные ряды
разложены в степенные ряды
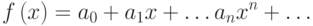 |
(
9.12)
|
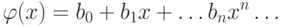 |
(
9.13)
|
Тогда
Оказывается, что слагаемые в правой части равенства можно переставить и
сгруппировать вместе члены с одинаковыми степенями

.
Это утверждение
совсем не так очевидно, как кажется на первый взгляд. Ведь в
правой части равенства у нас бесконечные суммы, а в бесконечных суммах
переставлять слагаемые можно далеко не всегда. После этой
перегруппировки мы получим
 |
(
9.14)
|
Ряд, стоящий в правой части равенства (9.14), называется
суммой степенных рядов (9.12) и (9.13).
Посмотрим теперь, как разлагается в степенной ряд произведение функций  и
и 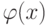 . Мы имеем
. Мы имеем
 |
(
9.15)
|
Оказывается, что как и в случае многочленов, ряды, стоящие в правой части
равенства (9.15), можно почленно перемножать. Мы опускаем
доказательство этого
утверждения. Найдем ряд, получающийся после почленного перемножения. Свободный член этого
ряда равен

. Члены, содержащие

, получатся
дважды: при умножении
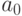
на

и при умножении

на

. Они дают
Точно так же вычисляются члены, содержащие
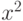
. Таким образом,
 |
(
9.16)
|
Ряд, стоящий в правой части равенства (9.16), называется
произведением рядов (9.12) и (9.13).
В частности, возводя ряд (9.12) в квадрат, получаем
 |
(
9.17)
|
Посмотрим теперь, как делят друг на друга степенные ряды. Пусть свободный
член ряда (9.13) отличен от нуля. Покажем, что в этом случае существует такой
степенной ряд
 |
(
9.18)
|
что
 |
(
9.19)
|
Для доказательства перемножим ряды в левой части этого равенства. Мы
получим ряд
Для того чтобы этот ряд совпадал с рядом (9.12), необходимо и достаточно, чтобы
выполнялись равенства
Эти равенства дают бесконечную систему уравнений для отыскания коэффициентов
Из первого уравнения системы получаем

. Подставим полученное
значение во второе уравнение. Мы получим
уравнение
из которого находим, что

. Вообще, если уже найдены
коэффициенты 
, то для отыскания
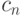
имеем уравнение
Это уравнение разрешимо, поскольку

.Итак, мы доказали существование
ряда (9.18), удовлетворяющего соотношению
(9.19). Ряд (9.18) называют
частным при делении рядов (9.12) и (9.13). Можно
доказать, что он получается при разложении функции

. Таким образом,
степенные ряды можно складывать, умножать и делить
(последнее - при условии, что свободный член делителя отличается от нуля). Эти действия
соответствуют действиям над разлагаемыми функциями.
 и
и 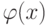 разложены в степенные ряды
разложены в степенные ряды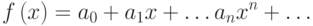
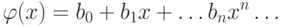

 . Это утверждение
совсем не так очевидно, как кажется на первый взгляд. Ведь в
правой части равенства у нас бесконечные суммы, а в бесконечных суммах
переставлять слагаемые можно далеко не всегда. После этой
перегруппировки мы получим
. Это утверждение
совсем не так очевидно, как кажется на первый взгляд. Ведь в
правой части равенства у нас бесконечные суммы, а в бесконечных суммах
переставлять слагаемые можно далеко не всегда. После этой
перегруппировки мы получим
 и
и 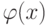 . Мы имеем
. Мы имеем
 . Члены, содержащие
. Члены, содержащие  , получатся
дважды: при умножении
, получатся
дважды: при умножении 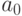 на
на  и при умножении
и при умножении  на
на  . Они дают
. Они дают
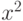 . Таким образом,
. Таким образом,









 . Подставим полученное значение во второе уравнение. Мы получим
уравнение
. Подставим полученное значение во второе уравнение. Мы получим
уравнение
 . Вообще, если уже найдены коэффициенты
. Вообще, если уже найдены коэффициенты  , то для отыскания
, то для отыскания 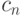 имеем уравнение
имеем уравнение
 .Итак, мы доказали существование
ряда (9.18), удовлетворяющего соотношению
(9.19). Ряд (9.18) называют частным при делении рядов (9.12) и (9.13). Можно
доказать, что он получается при разложении функции
.Итак, мы доказали существование
ряда (9.18), удовлетворяющего соотношению
(9.19). Ряд (9.18) называют частным при делении рядов (9.12) и (9.13). Можно
доказать, что он получается при разложении функции  . Таким образом, степенные ряды можно складывать, умножать и делить
(последнее - при условии, что свободный член делителя отличается от нуля). Эти действия
соответствуют действиям над разлагаемыми функциями.
. Таким образом, степенные ряды можно складывать, умножать и делить
(последнее - при условии, что свободный член делителя отличается от нуля). Эти действия
соответствуют действиям над разлагаемыми функциями.