| Россия |
Последовательности (множества и мультимножества)
Решето Эратосфена
Одной из самых больших загадок математики является расположение
простых чисел в ряду всех натуральных чисел. Иногда два простых числа идут
через одно, (например, 17 и 19, 29 и 31), а иногда подряд идет миллион
составных чисел. Сейчас ученые знают уже довольно много о том, сколько
простых чисел содержится среди  первых натуральных чисел. В этих
подсчетах весьма полезным оказался метод, восходящий еще к
древнегреческому ученому Эратосфену. Он жил в третьем веке до новой эры в
Александрии.
первых натуральных чисел. В этих
подсчетах весьма полезным оказался метод, восходящий еще к
древнегреческому ученому Эратосфену. Он жил в третьем веке до новой эры в
Александрии.
Эратосфен занимался самыми различными вопросами - ему принадлежат интересные исследования в области математики, астрономии и других наук. Впрочем, такая разносторонность привела его к некоторой поверхностности. Современники несколько иронически называли Эратосфена "во всем второй": второй математик после Евклида, второй астроном после Гиппарха и т.д.
В математике Эратосфена интересовал как раз вопрос о том, как найти все
простые числа среди натуральных чисел от 1 до  . (Эратосфен
считал 1 простым числом. Сейчас математики считают 1 числом особого
вида, которое не относится ни к простым, ни к составным числам.) Он придумал
для этого следующий способ. Сначала вычеркивают все числа, делящиеся на 2 (исключая
само число 2). Потом берут первое из оставшихся чисел (а именно 3). Ясно, что
это число - простое. Вычеркивают все идущие после него числа, делящиеся на 3.
Первым оставшимся числом будет 5. Вычеркивают все идущие после него числа, делящиеся
на 5, и т.д. Числа, которые уцелеют после всех вычеркиваний, и являются простыми.
Так как во времена Эратосфена писали на восковых табличках и не вычеркивали, а
"выкалывали" цифры, то табличка после описанного процесса напоминала решето.
Поэтому метод Эратосфена для нахождения простых чисел получил название
"решето Эратосфена".
. (Эратосфен
считал 1 простым числом. Сейчас математики считают 1 числом особого
вида, которое не относится ни к простым, ни к составным числам.) Он придумал
для этого следующий способ. Сначала вычеркивают все числа, делящиеся на 2 (исключая
само число 2). Потом берут первое из оставшихся чисел (а именно 3). Ясно, что
это число - простое. Вычеркивают все идущие после него числа, делящиеся на 3.
Первым оставшимся числом будет 5. Вычеркивают все идущие после него числа, делящиеся
на 5, и т.д. Числа, которые уцелеют после всех вычеркиваний, и являются простыми.
Так как во времена Эратосфена писали на восковых табличках и не вычеркивали, а
"выкалывали" цифры, то табличка после описанного процесса напоминала решето.
Поэтому метод Эратосфена для нахождения простых чисел получил название
"решето Эратосфена".
Подсчитаем, сколько останется чисел в первой сотне, если мы вычеркнем по методу Эратосфена числа, делящиеся на 2, 3 и 5. Иными словами, поставим такой вопрос: сколько чисел в первой сотне не делится ни на одно из чисел 2, 3, 5? Эта задача решается по формуле включения и исключения.
Обозначим через 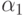 свойство числа делиться на 2, через
свойство числа делиться на 2, через 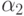 - свойство делимости на 3 и через
- свойство делимости на 3 и через 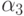 - свойство делимости на 5. Тогда
- свойство делимости на 5. Тогда  означает, что число делится на 6,
означает, что число делится на 6,  означает,
что оно делится на 10, и
означает,
что оно делится на 10, и 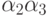 - оно делится на
15. Наконец,
- оно делится на
15. Наконец, 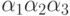 означает, что число
делится на 30. Надо найти, сколько чисел от 1 до 100 не делится
ни на 2, ни на 3, ни на 5, то есть не обладает ни одним из свойств
означает, что число
делится на 30. Надо найти, сколько чисел от 1 до 100 не делится
ни на 2, ни на 3, ни на 5, то есть не обладает ни одним из свойств 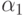 ,
, 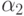 ,
, 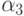 . По
формуле 6.3 имеем
. По
формуле 6.3 имеем
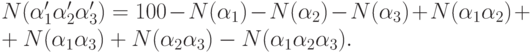
 делится на
делится на  , надо разделить
, надо разделить  на
на  и взять целую
часть получившегося частного. Поэтому
и взять целую
часть получившегося частного. Поэтому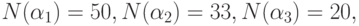
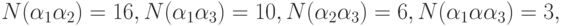

А из первой тысячи после первых трех шагов процесса Эратосфена останется 335 чисел. Это следует из того, что в этом случае
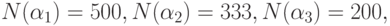

Примеры программы
Программа 1. Решето Эратосфена.
{В примере, иллюстрирующем работу с множествами, реализуется алгоритм
выделения из первой сотни натуральных чисел всех простых чисел. В основе
алгоритма лежит прием "решета Эратосфена".
Алгоритм написан на языке программирования Turbo-Pascal.}
Uses crt;
Const
N=100; {количество элементов исходного множества}
Type
SetN=set of 1..N;
var
n1, next, I : word; {вспомогательные переменные }
BeginSet, {исходное множество }
PrimerSet: SetN; {множество простых чисел }
Begin
Clrscr; {почистить экран}
BeginSet:=[2..N]; {создать исходное множество}
PrimerSet:=[1]; {первое простое число}
next:=2; {следующее простое число}
while BeginSet <> [ ] do {начало основного цикла}
begin
n1:=next; {n1-число, кратное очередному простому (next)}
while n1<=N do
{цикл удаления из исходного множества непростых чисел}
begin
BeginSet:=BeginSet-[n1];
n1:=n1+next {следующее кратное}
end; {конец цикла удаления}
repeat {получить следующее простое число, которое есть первое
не вычеркнутое из исходного множества}
inc(next)
until(next in BeginSet) or (next > N)
end; {конец основного цикла}
{вывод результата}
textcolor(15); {задание цвета}
for I:=1 to N do
if i in PrimerSet then write(I:8);
readln;
end.Программа 2. Простые числа в порядке убывания от 200.
{Находит и пишет все простые числа в порядке убывания от 2 до 200.
Алгоритм написан на языке программирования Turbo-Pascal.}
Uses crt;
const
n=197;
var
i,q,w,e,r,t:integer;
prost:array[1..n] of integer;
begin
clrscr;
e:=1;
r:=0;
for q:=1 to n do begin
r:=0;
for w:=2 to n-1 do
if (q<>w) and (q mod w = 0) then r:=1;
{prost[e]:=q; e:=e+1;}
if r=0 then begin{begin write(q,' ');}
prost[e]:=q;
e:=e+1;
end;
end;
for i:=e downto 2 do begin
write (prost[i],' ');
if wherex>70 then writeln;
end;
readln;
end.Программа 3. Поиск литер в строке.
{Поиск числа вхождений в данную сроку литер a, c, e, h.
Алгоритм написан на языке программирования Turbo-Pascal.}
Uses crt;
type
liter_set = set of char;
var
c:integer;
let: liter_set;
a:char;
begin
clrscr;
let:=['a','c','e','h'];
repeat
a:=readkey;
write(a);
if a in let then c:=c+1;
until a = '.';
writeln;
writeln('Общее число вхожений литер a,c,e,h в вашу запись:',c);
readln;
end.