| Россия |
Комбинаторика разбиений
Число сочетаний
Рассмотрим подмножества множества, состоящего из пяти элементов, и
подсчитаем их число. При этом записывать подмножества будем не с помощью букв,
как обычно, а в виде последовательностей длиной пять, составленных из нулей и
единиц. Каждая из единиц указывает на наличие в подмножестве соответствующего
элемента. Например, подмножества, содержащие один элемент, будут изображаться
следующими последовательностями: 10000, 01000, 00100, 00010, 00001. Пустое
подмножество  будет соответствовать последовательности
00000. Подмножества, содержащие по два элемента из пяти, запишутся с помощью
следующих последовательностей: 11000, 10100, 10010, 10001, 01100. 01010, 01001,
00110, 00101, 00011. Всего их
будет соответствовать последовательности
00000. Подмножества, содержащие по два элемента из пяти, запишутся с помощью
следующих последовательностей: 11000, 10100, 10010, 10001, 01100. 01010, 01001,
00110, 00101, 00011. Всего их 
Вообще, число сочетаний из  элементов по
элементов по  равно
числу всевозможных последовательностей из
равно
числу всевозможных последовательностей из  единиц и
единиц и  нулей.
нулей.
Задачи на разбиение чисел
Теперь мы переходим к задачам, в которых все разделяемые предметы совершенно одинаковы. В этом случае можно говорить не о разделении предметов, а о разбиении натуральных чисел на слагаемые (которые, конечно, тоже должны быть натуральными числами).
Здесь возникает много различных задач. В одних задачах учитывается порядок слагаемых, в других - нет.
Задача 4. Отправка бандероли.
За пересылку бандероли надо уплатить 18 рублей. Сколькими способами можно оплатить ее марками стоимостью 4, 6, и 10 рублей, если два способа, отличающиеся порядком марок, считаются различными (запас марок различного достоинства считаем неограниченным)?
Обозначим через 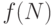 число способов, которыми можно наклеить
марки в 4, 6 и 10 рублей так, чтобы общая стоимость этих марок равнялась
число способов, которыми можно наклеить
марки в 4, 6 и 10 рублей так, чтобы общая стоимость этих марок равнялась 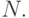 Тогда
для
Тогда
для 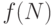 справедливо следующее соотношение:
справедливо следующее соотношение:
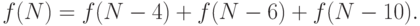 |
( 5.4) |
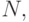 и пусть последней наклеена марка стоимостью 4 рубля. Тогда все остальные марки
стоят (
и пусть последней наклеена марка стоимостью 4 рубля. Тогда все остальные марки
стоят ( 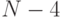 ) рубля. Наоборот, присоединяя к любой комбинации
марок общей стоимостью (
) рубля. Наоборот, присоединяя к любой комбинации
марок общей стоимостью ( 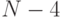 ) рубля одну четырехрублевую марку,
получаем комбинацию марок стоимостью
) рубля одну четырехрублевую марку,
получаем комбинацию марок стоимостью  рублей. При этом из разных
комбинаций стоимостью (
рублей. При этом из разных
комбинаций стоимостью ( 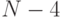 ) рублей получается разные комбинации
стоимостью
) рублей получается разные комбинации
стоимостью  рублей. Итак, число искомых комбинаций, где последней
наклеена марка стоимостью 4 рубля, равно
рублей. Итак, число искомых комбинаций, где последней
наклеена марка стоимостью 4 рубля, равно 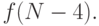
Точно так же доказывается, что число комбинаций, оканчивающихся на
шестирублевую марку, равно 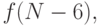 а на десятирублевую марку
оканчиваются
а на десятирублевую марку
оканчиваются 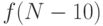 комбинацией. Поскольку любая комбинация
оканчивается на марку одного из указанных типов, то по правилу суммы получаем соотношение 5.4.
комбинацией. Поскольку любая комбинация
оканчивается на марку одного из указанных типов, то по правилу суммы получаем соотношение 5.4.
Соотношение 5.4 позволяет свести задачу о наклеивании марок на
сумму  рублей к задачам о наклеивании марок на меньшие суммы. Но
при малых значениях
рублей к задачам о наклеивании марок на меньшие суммы. Но
при малых значениях  задачу легко решить непосредственно. Простой
подсчет показывает, что
задачу легко решить непосредственно. Простой
подсчет показывает, что
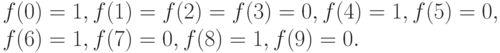
 означает, что сумму в 0 рублей можно уплатить
единственным образом: совсем не наклеивая марок. А сумму в 1,2,3,5,7 и 9
рублей вообще никак нельзя получить с помощью марок стоимостью 4, 6 и 10 рублей.
Используя значения
означает, что сумму в 0 рублей можно уплатить
единственным образом: совсем не наклеивая марок. А сумму в 1,2,3,5,7 и 9
рублей вообще никак нельзя получить с помощью марок стоимостью 4, 6 и 10 рублей.
Используя значения 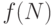 для
для 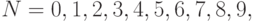 легко
найти
легко
найти 
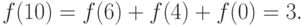
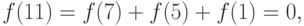
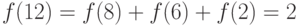
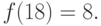 Таким образом, марки можно
наклеить восемью способами. Эти способы таковы:
Таким образом, марки можно
наклеить восемью способами. Эти способы таковы: 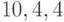 ;
;  ;
; 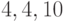 ;
;  ;
; 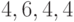 ;
; 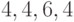 ;
; 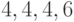 ;
; 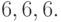 Отметим,
что значения
Отметим,
что значения 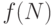 для
для 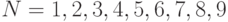 можно было
получить иначе, не приводя непосредственно проверки. Дело в том, что при
можно было
получить иначе, не приводя непосредственно проверки. Дело в том, что при  имеем
имеем 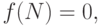 поскольку отрицательную сумму нельзя
уплатить, наклеивая неотрицательное количество марок. В то же время, как мы
видели,
поскольку отрицательную сумму нельзя
уплатить, наклеивая неотрицательное количество марок. В то же время, как мы
видели,  Поэтому
Поэтому 
Точно так же получаем значение  а для
а для 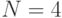 имеем
имеем 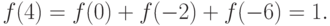
Задача 5.Общая задача о наклейке марок.
Разобранная задача является частным случаем следующей общей задачи: Имеются марки достоинством в 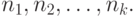 Сколькими
способами можно оплатить с их помощью сумму в
Сколькими
способами можно оплатить с их помощью сумму в  рублей, если два
способа, отличающиеся порядком, считаются различными? Все числа
рублей, если два
способа, отличающиеся порядком, считаются различными? Все числа 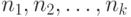 различны, а запас марок неограничен. Здесь на первом месте
мы будем указывать число слагаемых, на втором – разбиваемое число и на
последнем - ограничения на величину слагаемых.
различны, а запас марок неограничен. Здесь на первом месте
мы будем указывать число слагаемых, на втором – разбиваемое число и на
последнем - ограничения на величину слагаемых.
В этом случае число 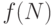 способов удовлетворяет соотношению
способов удовлетворяет соотношению
 |
( 5.5) |
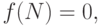 если
если  и
и  С помощью соотношения 5.5 можно найти
С помощью соотношения 5.5 можно найти 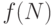 для любого
для любого 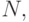 последовательно вычисляя
последовательно вычисляя 
Рассмотрим частный случай этой задачи, когда 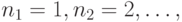
 Мы получаем всевозможные разбиения
числа
Мы получаем всевозможные разбиения
числа  на слагаемые
на слагаемые 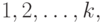 причем разбиения,
отличающиеся порядком слагаемых, считаются различными. Обозначим число
этих разбиений через
причем разбиения,
отличающиеся порядком слагаемых, считаются различными. Обозначим число
этих разбиений через 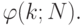 ( На первом месте мы будем указывать число слагаемых, на втором -
разбиваемое число и на последнем – ограничения на величину слагаемых.) Из
соотношения 5.5 следует, что
( На первом месте мы будем указывать число слагаемых, на втором -
разбиваемое число и на последнем – ограничения на величину слагаемых.) Из
соотношения 5.5 следует, что
 |
( 5.6) |
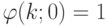 и
и 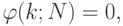 если
если  Вычисление
Вычисление 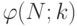 можно упростить, если заметить, что
можно упростить, если заметить, что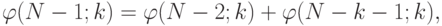
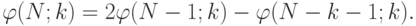 |
( 5.7) |
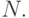 Поэтому
Поэтому 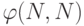 равно числу всех разбиений на
равно числу всех разбиений на  на натуральные слагаемые (включая и
"разбиение"
на натуральные слагаемые (включая и
"разбиение" 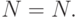 Если число слагаемых равно
Если число слагаемых равно  то получаем
то получаем  разбиений. Поэтому
разбиений. Поэтому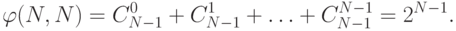
 можно разбить на
слагаемые
можно разбить на
слагаемые 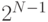 способами. Напомним, что при этом учитывается
порядок слагаемых.Например, число 5 можно разбить на слагаемые
способами. Напомним, что при этом учитывается
порядок слагаемых.Например, число 5 можно разбить на слагаемые  способами.
способами.| 5 = 5 | 5 = 3 + 1 + 1 | 5 = 1 + 2 + 2 |
| 5 = 4 + 1 | 5 = 1 + 3+ 1 | 5 = 2 + 1 + 1 + 1 |
| 5 = 1 + 4 | 5 = 1 + 1 + 3 | 5 = 1 + 2 + 1 + 1 |
| 5 = 2 + 3 | 5 = 2 + 2 + 1 | 5 = 1 + 1 + 2 + 1 |
| 5 = 3 + 2 | 5 = 2 + 1 + 2 | 5 = 1 + 1 + 1 + 2 |
| 5 = 1 + 1 + 1 + 1 + 1 |
Комбинаторные задачи теории информации
Информация - сведения, неизвестные до их получения, или данные, или значения, приписанные данным.
Теория информации - математическая дисциплина, изучающая количественные свойства информации.
Задачу, похожую на только что решенную, приходится решать в теории
информации. Предположим, что сообщение передается с помощью сигналов
нескольких типов. Длительность передачи сигнала первого типа
равна 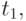 второго типа -
второго типа - 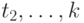 -го типа
-
-го типа
-  единиц времени.
единиц времени.
Задача 6. Сколько различных сообщений можно передать с помощью этих сигналов
за  единиц времени? При этом учитываются лишь "максимальные" сообщения,
то есть сообщения, к которым нельзя присоединить ни одного сигнала, не выйдя за рамки
отведенного для передачи времени.
единиц времени? При этом учитываются лишь "максимальные" сообщения,
то есть сообщения, к которым нельзя присоединить ни одного сигнала, не выйдя за рамки
отведенного для передачи времени.
Обозначим число сообщений, которые можно передать за время  через
через  Рассуждая точно так же, как и в задаче о марках, получаем,
что
Рассуждая точно так же, как и в задаче о марках, получаем,
что 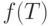 удовлетворяет соотношению
удовлетворяет соотношению
 |
( 5.8) |
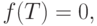 если
если  и
и  .
.