Решения задач
И, наконец, равенство (7.8) следует из того, что собственные числа оператора 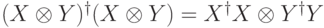 имеют вид
имеют вид 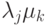 , где
, где 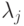 и
и 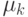 — собственные числа
— собственные числа 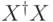 и
и 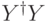 , соответственно.
, соответственно.
7.3. Достаточно проверить для двух сомножителей. Имеем

 , (
, (  ). Поэтому
). Поэтому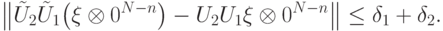
7.4 Обозначим  . Будем искать оператор в виде
. Будем искать оператор в виде ![W=(U\otimes I_{[n+1,\dots,N]})\Pi_\calM +\tilde W(I-\Pi_\calM)](/sites/default/files/tex_cache/12e2fb47fcb93845ff586b8c003e40c5.png) , где унитарный оператор
, где унитарный оператор  сохраняет
сохраняет 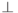 . Для такого
. Для такого  , очевидно, выполняется равенство
, очевидно, выполняется равенство

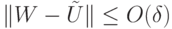 эквивалентно тому, что для всех
эквивалентно тому, что для всех  выполняется
выполняется 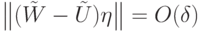 . Представляя
. Представляя 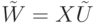 , получаем эквивалентные условия на унитарный оператор
, получаем эквивалентные условия на унитарный оператор  :
: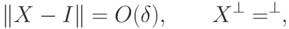
 .
.Теперь нам потребуется следующая лемма.
Лемма. Пусть  и
и  — подпространства конечномерного пространства
— подпространства конечномерного пространства  , такие что
, такие что 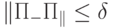 ,
,  . Тогда найдется унитарный оператор
. Тогда найдется унитарный оператор  , такой что
, такой что  и
и 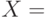 . (Значит, и
. (Значит, и 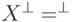 .)
.)
Доказательство. Возьмем оператор 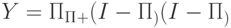 . Сразу видно, что он переводит
. Сразу видно, что он переводит  в
в  и
и 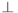 в
в 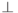 . Для нормы
. Для нормы 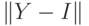 имеем оценку
имеем оценку
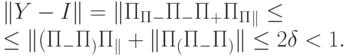
 не унитарный. Но из приведенной оценки следует, что он невырожденный. Рассмотрим унитарный оператор
не унитарный. Но из приведенной оценки следует, что он невырожденный. Рассмотрим унитарный оператор 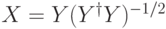 . Оператор
. Оператор 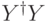 сохраняет подпространство
сохраняет подпространство  , поэтому
, поэтому  переводит
переводит  в
в  . Для оценки нормы
. Для оценки нормы  разложим
разложим 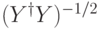 в ряд Тейлора
в ряд Тейлора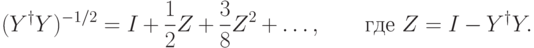
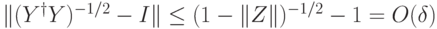 , отсюда получаем
, отсюда получаем  .
.Чтобы применить лемму, необходимо оценить величину  . Имеем
. Имеем  (
(  приближает
приближает  в расширенном смысле с точностью
в расширенном смысле с точностью  ). Обозначая
). Обозначая 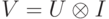 , получаем
, получаем

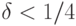 .
.7.5 Схему для оператора 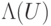 можно построить, используя элемент Фредкина
можно построить, используя элемент Фредкина 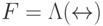 — управляемый обмен битами. Элемент Фредкина задается соотношениями
— управляемый обмен битами. Элемент Фредкина задается соотношениями

![F[1,2,3]=\Lambda(\qxor)[1,2,3]\ \Lambda(\qxor)[1,3,2]\ \Lambda(\qxor)[1,2,3]](/sites/default/files/tex_cache/8db3dd59aa3977398781fcd7a793d4cf.png)
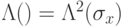 — это элемент Тоффоли).
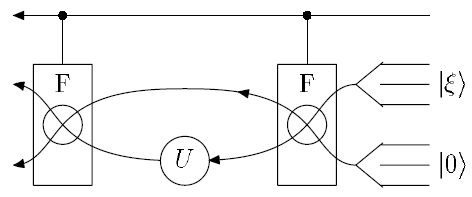
— это элемент Тоффоли).На рис. 15.7 показано, как из схемы для оператора  , сохраняющего
, сохраняющего  , построить схему для
, построить схему для 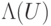 . В прямоугольниках происходит управляемый обмен q-битами (параллельно действует нужное количество элементов Фредкина). Если управляющий q-бит равен
. В прямоугольниках происходит управляемый обмен q-битами (параллельно действует нужное количество элементов Фредкина). Если управляющий q-бит равен 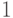 , то на вход схемы, вычисляющей
, то на вход схемы, вычисляющей  , будет подан
, будет подан 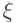 , в противном случае —
, в противном случае —  .
.
7.6 Каждый из рассматриваемых поворотов порождает всюду плотное подмножество в подгруппе поворотов относительно фиксированной прямой. Поэтому осталось доказать, что повороты относительно двух различных прямых порождают  . Для этого достаточно доказать, что подгруппа, порожденная всеми поворотами относительно двух различных прямых, действует транзитивно на сфере (или на проективной плоскости — множестве одномерных подпространств). Справедливость этого факта очевидна из рис. 15.8 (если можно перемещаться по двум семействам параллелей, то из любой точки на сфере можно попасть в любую другую). Строгое доказательство получается аналогично решению задачи 7.7.
. Для этого достаточно доказать, что подгруппа, порожденная всеми поворотами относительно двух различных прямых, действует транзитивно на сфере (или на проективной плоскости — множестве одномерных подпространств). Справедливость этого факта очевидна из рис. 15.8 (если можно перемещаться по двум семействам параллелей, то из любой точки на сфере можно попасть в любую другую). Строгое доказательство получается аналогично решению задачи 7.7.
Замечание. Это решение неконструктивно: нельзя дать никакой верхней оценки на количество поворотов 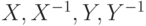 , композиция которых приближает заданный элемент
, композиция которых приближает заданный элемент  с заданной точностью
с заданной точностью  . Причина неконструктивности состоит в следующем. Поворот на угол
. Причина неконструктивности состоит в следующем. Поворот на угол  , где
, где  — иррациональное, порождает всюду плотное подмножество в группе поворотов относительно фиксированной прямой (эта группа, очевидно, изоморфна
— иррациональное, порождает всюду плотное подмножество в группе поворотов относительно фиксированной прямой (эта группа, очевидно, изоморфна  ). Однако число
). Однако число  может очень хорошо приближаться рациональными числами (это имеет место, когда коэффициенты цепной дроби, представляющей
может очень хорошо приближаться рациональными числами (это имеет место, когда коэффициенты цепной дроби, представляющей  , очень быстро растут). Тогда любое
, очень быстро растут). Тогда любое  приближается элементами вида
приближается элементами вида 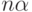 (
(  ) с любой точностью
) с любой точностью 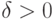 , но число
, но число  может быть сколь угодно велико: больше, чем любая наперед заданная функция
может быть сколь угодно велико: больше, чем любая наперед заданная функция  .
.
Конструктивное доказательство и эффективный (при фиксированных  и
и  ) алгоритм построения аппроксимаций довольно сложны [4].
) алгоритм построения аппроксимаций довольно сложны [4].
7.7 Обозначим 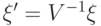 , тогда
, тогда 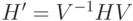 — стабилизатор
— стабилизатор 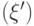 . Так что утверждение задачи приобретает вид: объединение стабилизаторов двух несовпадающих одномерных подпространств порождает
. Так что утверждение задачи приобретает вид: объединение стабилизаторов двух несовпадающих одномерных подпространств порождает 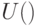 .
.
Достаточно показать, что группа  , порожденная
, порожденная 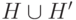 , действует транзитивно на множестве единичных векторов. Действительно, пусть для каждого
, действует транзитивно на множестве единичных векторов. Действительно, пусть для каждого 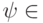 найдется оператор
найдется оператор 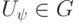 , такой что
, такой что 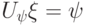 . Тогда
. Тогда

Доказываем транзитивность действия группы  . Заметим, что
. Заметим, что
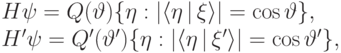
где 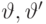 обозначают углы между
обозначают углы между 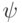 и
и 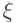 ,
, 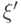 соответственно:
соответственно:  ,
,  ,
, 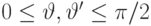 . В последующих формулах используется также угол
. В последующих формулах используется также угол  между векторами
между векторами 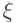 и
и 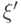 :
:  ,\,
,\, 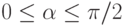 .
.
Можно проверить, что при 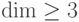

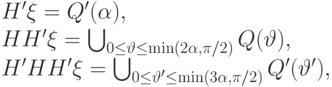
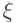 попеременно элементами из
попеременно элементами из 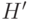 и
и  достаточное количество раз, можно получить любой единичный вектор
достаточное количество раз, можно получить любой единичный вектор 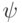 .
.7.8 Поскольку 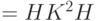 , то стандартный базис содержит полный базис для классических обратимых вычислений (см. задачу 6.1). Это, благодаря задаче 7.5, позволяет реализовать операторы
, то стандартный базис содержит полный базис для классических обратимых вычислений (см. задачу 6.1). Это, благодаря задаче 7.5, позволяет реализовать операторы 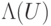 для всех элементов базиса, кроме
для всех элементов базиса, кроме  .
.
Теперь рассмотрим оператор 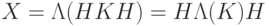 , который, в силу сказанного, реализуется в стандартном базисе (оператор
, который, в силу сказанного, реализуется в стандартном базисе (оператор  сохраняет
сохраняет  ). Подействуем им на
). Подействуем им на  двумя возможными способами:
двумя возможными способами: ![X_1=X[1,2]](/sites/default/files/tex_cache/59aa2228833bcc9815b0b0ea427ea218.png) ,
, ![X_2=X[2,1]](/sites/default/files/tex_cache/1e8ba9d495198b80f89db020ec4c4c0a.png) . Операторы
. Операторы 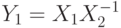 ,
, 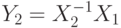 также реализуются в стандартном базисе.
также реализуются в стандартном базисе.
Заметим, что операторы  ,
,  (следовательно, и
(следовательно, и 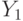 ,
, 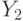 ) сохраняют векторы
) сохраняют векторы  и
и  . Кроме того, вычислениями проверяется, что
. Кроме того, вычислениями проверяется, что 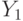 ,
, 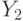 не коммутируют и имеют, помимо 1, собственные числа
не коммутируют и имеют, помимо 1, собственные числа  . В
. В 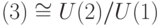 оператору с такими собственными числами соответствует поворот на угол
оператору с такими собственными числами соответствует поворот на угол  . Поскольку
. Поскольку 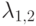 не являются корнями из
не являются корнями из  (и даже целыми алгебраическими числами, так как их след равен
(и даже целыми алгебраическими числами, так как их след равен 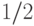 ), угол
), угол  несоизмерим с
несоизмерим с  . А поскольку эти операторы не коммутируют, им соответствуют повороты вокруг различных прямых. Поэтому
. А поскольку эти операторы не коммутируют, им соответствуют повороты вокруг различных прямых. Поэтому 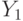 ,
, 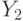 порождают всюду плотное подмножество в
порождают всюду плотное подмножество в  , где
, где 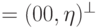 (см. задачу 7.6).
(см. задачу 7.6).
Для завершения доказательства дважды применим результат задачи 7.7. Операторы 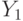 ,
, 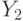 порождают всюду плотное множество в
порождают всюду плотное множество в  , оператор
, оператор 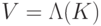 сохраняет
сохраняет 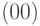 и не сохраняет
и не сохраняет  . Так что
. Так что 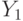 ,
, 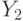 ,
, 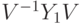 ,
, 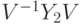 порождают всюду плотное множество в
порождают всюду плотное множество в 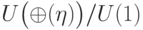 . Оператор
. Оператор ![H[1]](/sites/default/files/tex_cache/9ee660f8c5ac88dc78a6200d677a6b43.png) не сохраняет
не сохраняет 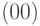 ; применяя результат задачи 7.7 еще раз, получаем всюду плотное множество в
; применяя результат задачи 7.7 еще раз, получаем всюду плотное множество в 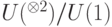 .
.
7.9 Из предыдущей задачи следует, что можно реализовать оператор 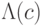 с точностью до фазового множителя,
с точностью до фазового множителя,  . Оператор
. Оператор  реализуется точно. Возьмем дополнительный q-бит в состоянии
реализуется точно. Возьмем дополнительный q-бит в состоянии  и применим
и применим  . Неизвестный фазовый множитель сокращается.
. Неизвестный фазовый множитель сокращается.
7.10 В базисе 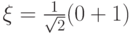 ,
, 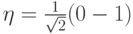 оператор
оператор  диагонализуется, так что в этом базисе
диагонализуется, так что в этом базисе  имеет вид
имеет вид
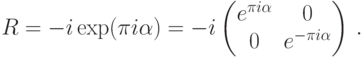
 — иррациональное число, степенями
— иррациональное число, степенями  можно приближенно реализовать любой оператор вида
можно приближенно реализовать любой оператор вида 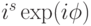 , который в указанном выше базисе имеет матрицу
, который в указанном выше базисе имеет матрицу 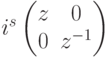 , где
, где 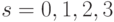 ,
,  . В геометрической интерпретации эти операторы соответствуют поворотам вокруг оси
. В геометрической интерпретации эти операторы соответствуют поворотам вокруг оси  . При
. При 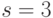 и
и 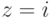 получаем элемент Тоффоли:
получаем элемент Тоффоли:  (при подходящем
(при подходящем  ), так что уже имеем полный классический базис. При
), так что уже имеем полный классический базис. При 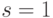 и
и 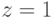 получаем
получаем 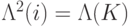 (на третий q-бит этот оператор действует тождественным образом). Из
(на третий q-бит этот оператор действует тождественным образом). Из 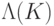 можно сделать
можно сделать  , подавая на управляющий q-бит константу
, подавая на управляющий q-бит константу 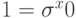 . С точностью до фазового множителя
. С точностью до фазового множителя  — это поворот на
— это поворот на  вокруг оси
вокруг оси  , а композициями поворотов вокруг
, а композициями поворотов вокруг  и одного поворота вокруг
и одного поворота вокруг  представляются все элементы
представляются все элементы  (аналогично задаче 7.7).
(аналогично задаче 7.7).Итак, мы получили реализацию всех операторов из  с точностью до фазового множителя. Осталось использовать задачу 7.9 для того, чтобы реализовать
с точностью до фазового множителя. Осталось использовать задачу 7.9 для того, чтобы реализовать  .
.
7.11 Любое вращение трехмерного пространства представляется как композиция трех поворотов: на угол  вокруг оси
вокруг оси  , затем на угол
, затем на угол  вокруг оси
вокруг оси  , затем на угол
, затем на угол  вокруг оси
вокруг оси  . Поэтому любой оператор, действующий на одном q-бите, представляется в виде
. Поэтому любой оператор, действующий на одном q-бите, представляется в виде
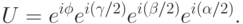 |
( *) |
Каждый из операторов в правой части  выражается через
выражается через  и управляемые фазовые сдвиги:
и управляемые фазовые сдвиги:
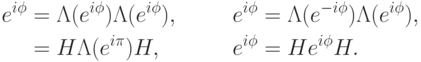
Таким образом, для решения задачи достаточно построить схему, представляющую управляемый фазовый сдвиг  с точностью
с точностью 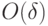 .
.
Выберем такое 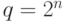 , что
, что  . Предположим, что у нас в распоряжении есть
. Предположим, что у нас в распоряжении есть  -битовый регистр в состоянии
-битовый регистр в состоянии
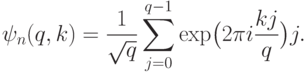
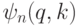 — собственный вектор классического оператора
— собственный вектор классического оператора 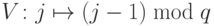 :
: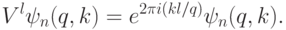
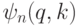 оператор
оператор  , управляемый дополнительным q-битом, получаем искомый фазовый сдвиг на этом q-бите:
, управляемый дополнительным q-битом, получаем искомый фазовый сдвиг на этом q-бите:
(Классический) оператор 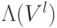 можно задать схемой линейного размера в стандартном базисе. Если
можно задать схемой линейного размера в стандартном базисе. Если  — нечетно, то выбором подходящего
— нечетно, то выбором подходящего  можно представить оператор
можно представить оператор  с точностью
с точностью 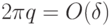 .
.
Вместо того, чтобы строить схему, порождающую 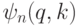 , будем брать смесь
, будем брать смесь 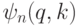 при разных
при разных  , измерять значение
, измерять значение  и выбирать
и выбирать  , соответствующее этому измеренному значению. Опишем требуемые действия.
, соответствующее этому измеренному значению. Опишем требуемые действия.
- Создаем векторЗаметим, что
![\sz[1] H[1]\ket{0^n}=\ket\eta= \frac{1}{\sqrt2}\ket{0}-\frac{1}{\sqrt2}\ket{q/2}= \frac{1}{\sqrt{q/2}}\sum_{s=0}^{q/2-1}\ket{\psi_n(q,2s+1)}.](/sites/default/files/tex_cache/803209bace323f28f87a743ecfd30795.png)
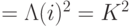 реализуется точно в стандартном базисе.
реализуется точно в стандартном базисе. - Произведем измерение
 с вероятностью ошибки
с вероятностью ошибки 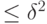 ; оно может быть представлено операторомгде
; оно может быть представлено операторомгде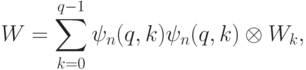
 , а векторы
, а векторы 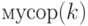 и
и 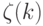 — единичной длины. Заметим, что точность — квадратный корень из вероятности ошибки:
— единичной длины. Заметим, что точность — квадратный корень из вероятности ошибки: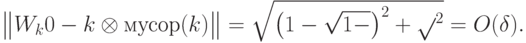
- Найдем такое
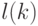 , что
, что 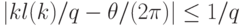 .
. - Применим
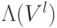 к рабочему
к рабочему  -битовому регистру, используя бит, в котором нужно сделать фазовый сдвиг, в качестве управляющего.
-битовому регистру, используя бит, в котором нужно сделать фазовый сдвиг, в качестве управляющего. - Обратим вычисления, сделанные на шагах 1 — 3.
Чтобы вероятность ошибки была меньше 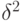 , нужны
, нужны  элементарных измерений для каждого из операторов
элементарных измерений для каждого из операторов  ,
, 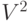
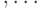 ,
, 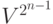 . Поскольку
. Поскольку  , общий размер схемы —
, общий размер схемы — 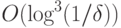 .
.