Решения задач
Из раздела 8
8.1 Пусть 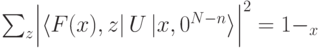 , и
, и 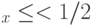 для всех
для всех  . Нам нужно оценить величину
. Нам нужно оценить величину
![p(x)=\mkern-15mu\sum_{\scriptstyle\begin{gathered} \scriptstyle f_1,\dots,f_k\\[-8pt] \scriptstyle z_1,\dots,z_k\end{gathered}}^{} \Bigl| \langle f_1,z_1,\dots,f_k,z_k, F(x), 0^{s} |\,MU^{\otimes k}\,| (x,0^{N-n})^{k}, 0^{m+s}\rangle \Bigr|^2,](/sites/default/files/tex_cache/e5be2a3c75ac6ac4d68251d7db592987.png)
 — оператор, реализующий применение функции MAJ к соответственным битам
— оператор, реализующий применение функции MAJ к соответственным битам  регистров ответа исходной схемы и записывающий значение этой функции в регистр окончательного ответа. (Длина ответа равна
регистров ответа исходной схемы и записывающий значение этой функции в регистр окончательного ответа. (Длина ответа равна  , а
, а  дополнительных битов используются при вычислении MAJ).
дополнительных битов используются при вычислении MAJ).Если более половины регистров ответа исходной схемы содержат  , то результатом применения
, то результатом применения  обязательно будет
обязательно будет  . Поэтому, аналогично (3.1), имеем
. Поэтому, аналогично (3.1), имеем
![\begin{multiline*} 1-p(x)\leq\\ \leq\mkern-5mu \sum_{\scriptstyle \begin{gathered} \scriptscriptstyle S\subseteq\{1,\dots,k\},\\[-7pt] \scriptscriptstyle|S|\leq k/2\end{gathered}} \sum_{\scriptstyle \begin{gathered} \scriptscriptstyle f_1,\dots,f_k,\\[-7pt] \scriptscriptstyle f_j=F(x)\,\Leftrightarrow\,j\in S\end{gathered}} \sum_{z_1,\dots,z_k} \Bigl| \langle f_1,z_1,\dots,f_k,z_k |U^{\otimes k}| (x,0^{N-n})^{k}\rangle \Bigr|^2=\\ =\mkern-5mu \sum_{\scriptstyle\begin{gathered} \scriptscriptstyle S\subseteq\{1,\dots,k\},\\[-6pt] \scriptscriptstyle|S|\leq k/2\end{gathered}} (1-\eps_x)^{|S|}\eps_x^{k-|S|}= \bigl((1-\eps_x)\eps_x\bigr)^{k/2} \sum_{\scriptstyle\begin{gathered} \scriptscriptstyle S\subseteq\{1,\dots,k\},\\[-6pt] \scriptscriptstyle|S|\leq k/2\end{gathered}} \left(\frac{\eps_x}{1-\eps_x}\right)^{k/2-|S|}\leq\\ \leq\left(\sqrt{(1-\eps_x)\eps_x}\right)^k 2^k\,\leq\,\lambda^k, \quad \text{где }\lambda=2\sqrt{(1-\eps)\eps.} \end{multiline*}](/sites/default/files/tex_cache/fcf8920e43017639f8f6cc77ffee990a.png)
8.2 Поскольку 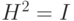 , имеем цепочку равенств:
, имеем цепочку равенств:
Оператор 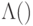 умножает
умножает 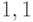 на
на  , а остальные базисные векторы не меняет.
, а остальные базисные векторы не меняет.
Если сделать замену базиса только в управляющем q-бите, как показано на рисунке ниже, то получится оператор, который является произведением отрицаний в обоих q-битах и "оператора диффузии" (в
"Определение квантового вычисления. Примеры"
мы обозначали его  ). Действительно,
). Действительно,
![\begin{equation*} H[1]\Lambda(\sx)[1,2]H[1]\ket{a,b}&= H[1]\Lambda(\sx)[1,2] \frac{1}{\sqrt2}\sum_{c}^{}(-1)^{ac}\ket{c,b}=\\ =H[1]\frac{1}{\sqrt2}\sum_{c}^{}(-1)^{ac}\ket{c,b\oplus c}&= \frac{1}{2}\sum_{c,d}^{}(-1)^{(a+d)c}\ket{d,b\oplus c}=\\ &=\frac{1}{2}\sum_{c,b'}^{}(-1)^{(a+d)(b+b')}\ket{d,b'}. \end{equation*}](/sites/default/files/tex_cache/446f77f0dda8786dcaa4cd5d58779f37.png)
На рисунке слева показана схема вычисления такого оператора, а справа — его матрица в стандартном базисе:
8.3  . Классическое вероятностное вычисление можно представить обратимой схемой
. Классическое вероятностное вычисление можно представить обратимой схемой 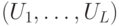 , которая, наряду со входом
, которая, наряду со входом  , использует случайную последовательность нулей и единиц
, использует случайную последовательность нулей и единиц 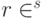 . (Кроме полезного ответа, схема может создавать мусор — это неважно). Заменим перестановки
. (Кроме полезного ответа, схема может создавать мусор — это неважно). Заменим перестановки 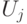 на соответствующие унитарные операторы
на соответствующие унитарные операторы 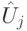 , а вместо случайного слова
, а вместо случайного слова  приготовим состояние
приготовим состояние
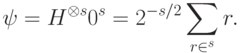
 . Пусть схема
. Пусть схема 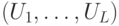 вычисляет предикат
вычисляет предикат  с вероятностью ошибки
с вероятностью ошибки 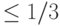 , общее число битов в схеме равно
, общее число битов в схеме равно  , а
, а 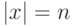 . Вероятность получения ответа 1 выражается через проектор
. Вероятность получения ответа 1 выражается через проектор  , примененный к первому q-биту:
, примененный к первому q-биту:
![\begin{equation*} p(x) =\,& \langle x,0^{N-n} | U_1^\dagger U_2^\dagger\cdot\ldots\cdot U_L^\dagger \,\Pi^{(1)}[1]\, U_LU_{L-1}\cdot\ldots\cdot U_1 | x,0^{N-n} \rangle =\\ =\,& 2^{-h} \langle x,0^{N-n} | V_{L}V_{L-1}\cdot\ldots\cdot V_{-L+1}V_{-L} | x,0^{N-n} \rangle. \end{equation*}](/sites/default/files/tex_cache/4deaa66494480310e4b0da60b4b51749.png) |
( *) |
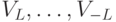 — перенумерованные операторы
— перенумерованные операторы ![U_1^\dagger,\dots,\Pi^{(1)}[1],\dots](/sites/default/files/tex_cache/140c1d86f24b847afc476b268c6db542.png)
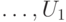 с одним исключением: если
с одним исключением: если ![U_k=H[m]](/sites/default/files/tex_cache/91141776d5fe78191cffb67426d6cf25.png) (или
(или ![U_k^\dagger=H[m]](/sites/default/files/tex_cache/d5f4640e7046f279740dd11155bb8fd3.png) ), то соответствующий оператор
), то соответствующий оператор 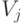 равен
равен ![\sqrt{2}H[m]](/sites/default/files/tex_cache/d615ee411f3239a16c2bf4f0fc503a17.png) ; количество элементов
; количество элементов  в схеме обозначено через
в схеме обозначено через  .
.Матричные элементы операторов 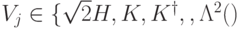 ,
,  принадлежат множеству
принадлежат множеству
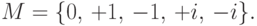
 . Поскольку интересующая нас величина
. Поскольку интересующая нас величина 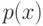 вещественная, мы можем ограничиться суммированием
вещественная, мы можем ограничиться суммированием  . Кратности слагаемых будут выражаться в виде
. Кратности слагаемых будут выражаться в виде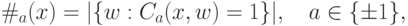
 определены ниже. Получаем представление
определены ниже. Получаем представление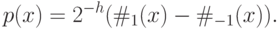
 к виду из определения класса PPP уже не будет использовать никакой квантовой специфики.
к виду из определения класса PPP уже не будет использовать никакой квантовой специфики.Теперь опишем предикаты 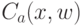 формально. Матричные элементы произведения
формально. Матричные элементы произведения  можно выразить по формуле (5.1)
можно выразить по формуле (5.1)

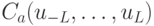 равно 1, если и только если
равно 1, если и только если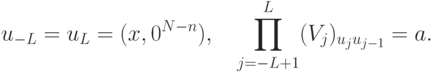
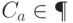 : нужно представлять матричные элементы как степени
: нужно представлять матричные элементы как степени  и суммировать показатели степеней по модулю 4.
и суммировать показатели степеней по модулю 4.Если 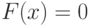 , то
, то  ; если
; если  , то
, то  . Итак,
. Итак,  тогда и только тогда, когда
тогда и только тогда, когда
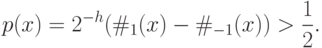

Записанное неравенство почти соответствует определению класса  : остается лишь проверить, что левая часть представима в виде
: остается лишь проверить, что левая часть представима в виде 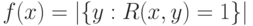 ,
, 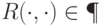 (для правой части это уже доказано). Функции
(для правой части это уже доказано). Функции  такого вида образуют так называемый класс
такого вида образуют так называемый класс 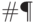 . Покажем, что этот класс замкнут относительно сложения. Пусть
. Покажем, что этот класс замкнут относительно сложения. Пусть 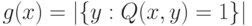 ,
, 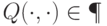 , тогда
, тогда
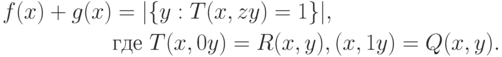
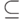 . Это очевидно. Заведем два счетчика: один для
. Это очевидно. Заведем два счетчика: один для 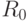 , другой — для
, другой — для 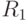 . Перебираем все возможные значения
. Перебираем все возможные значения  и увеличиваем значения счетчиков для
и увеличиваем значения счетчиков для 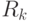 , если
, если 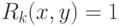 . Потом сравниваем значения счетчиков.
. Потом сравниваем значения счетчиков.
8.4 Пункт а) следует из пункта б). Для б) приведем схему, которая дает приближенное решение. Прежде всего, запишем рекуррентную формулу
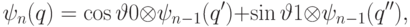
![&q'=2^{n-1}, & &q''=q-2^{n-1}, & &\vartheta=\arccos\sqrt{q'/q}, & &\text{если } q>2^{n-1}; \notag\\[-3pt] &q'=q, & &q''=1, & &\vartheta=0, & &\text{если } q\leq2^{n-1}. \notag](/sites/default/files/tex_cache/100d5e1f082acf734da6d2c3f730dfda.png)
Организуем рекурсивное вычисление, используя формулу  .
.
- Вычисляем
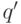 ,
, 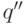 ,
, 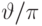 , последнее представляем приближенно
, последнее представляем приближенно  двоичными цифрами. Запоминаем результаты вычисления в дополнительных q-битах.
двоичными цифрами. Запоминаем результаты вычисления в дополнительных q-битах. - Применяем к первому q-биту регистра
 , в котором нужно создать
, в котором нужно создать 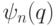 , оператор
, оператор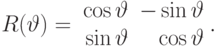
- В остальных
 битах создаем состояние, зависящее от значения первого бита: если он равен 0, то создаем состояние
битах создаем состояние, зависящее от значения первого бита: если он равен 0, то создаем состояние 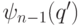 , в противном случае создаем
, в противном случае создаем 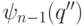 .
. - Проводим вычисление, обратное к шагу 1, чтобы очистить дополнительную память.
Оператор 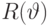 реализуется приближенно. Пусть
реализуется приближенно. Пусть 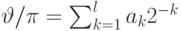 . Тогда
. Тогда 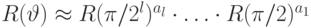 с точностью
с точностью 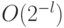 . Итак, приближенно оператор
. Итак, приближенно оператор 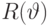 представляется произведением операторов
представляется произведением операторов 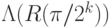 , где
, где  -й разряд числа
-й разряд числа 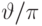 управляет применением оператора
управляет применением оператора 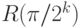 .
.
Общая точность такой схемы равна  ; размер, выраженный через длину входа и точность, —
; размер, выраженный через длину входа и точность, —  .
.
Пункт в). Приведем реализацию преобразования Фурье, найденную Копперсмитом и, независимо, Дойчем, в изложении П. Шора [39].
Занумеруем q-биты в убывающем порядке от  до
до  . Обозначим
. Обозначим
![H_j=H[j],\qquad S_{j,l}=\Lambda^2\bigl(e^{i\pi/2^{l-j}}\bigr)[j,l]\quad (j<l).](/sites/default/files/tex_cache/e141ded89468f8d854ffe6c4c70ecd24.png)
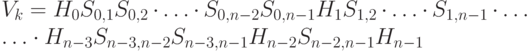
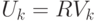 , где
, где  — (классический) оператор, переписывающий двоичное слово в обратном порядке. Размер такой схемы
— (классический) оператор, переписывающий двоичное слово в обратном порядке. Размер такой схемы 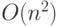 .
.Легко видеть, что модули матричных элементов 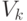 определяются количеством операторов
определяются количеством операторов 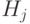 , так что они равны
, так что они равны 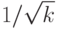 , как и требуется. Осталось проверить фазовые множители. Пусть
, как и требуется. Осталось проверить фазовые множители. Пусть

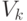 есть произведение матричных элементов сомножителей. Применение
есть произведение матричных элементов сомножителей. Применение 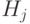 меняет фазу на
меняет фазу на  тогда и только тогда, когда
тогда и только тогда, когда 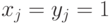 ; применение
; применение 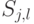 добавляет к фазе
добавляет к фазе 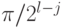 только в том случае, когда
только в том случае, когда 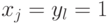 . Изменение фазы на
. Изменение фазы на 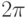 ни на что не влияет, поэтому вычислим
ни на что не влияет, поэтому вычислим  по модулю 1.
по модулю 1.![\begin{align*} &\phi(x_{n-1},\dots,x_0, y_{n-1},\dots,y_0) =\mkern-2mu\sum_{j=0}^{n-1}\frac{x_j y_j}{2}+\mkern-7mu \sum_{0\leq j<l<n}^{}\frac{x_j y_l}{2^{l-j+1}}=\\[-3pt] &=\mkern-7mu \sum_{0\leq j\leq l<n}^{}\frac{x_j y_l}{2^{l-j+1}}=\mkern-7mu \sum_{0\leq j+m<n}^{}\frac{x_j y_{n-1-m}}{2^{n-j-m}}=\\ \intertext{(здесь равенство по модулю 1)} &=\sum_{j,m=0}^{n-1} \frac{x_j y_{n-1-m}}{2^{n-j-m}} =2^{-n}\sum_{j=0}^{n-1}2^jx_j \sum_{m=0}^{n-1}2^my_{n-1-m}. \end{align*}](/sites/default/files/tex_cache/dfab0c41d46d9cbc90710d52b8b7efe8.png)
 в обратном порядке, последнее выражение превращается в
в обратном порядке, последнее выражение превращается в 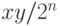 .
.

