Решения задач
Из раздела 11
11.1 По определению квантовой вероятности имеем
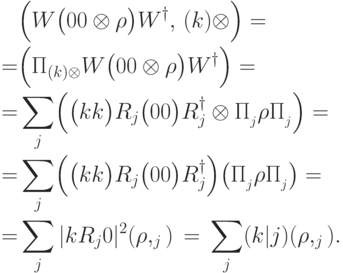
11.2 Если 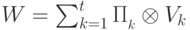 , то
, то 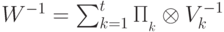 . Поэтому искомая квантовая схема имеет вид
. Поэтому искомая квантовая схема имеет вид  , где оператор
, где оператор  копирует в дополнительный регистр "полезный результат":
копирует в дополнительный регистр "полезный результат":
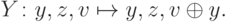
Из раздела 12
12.1 Интересующую нас вероятность обозначим через 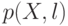 . Если
. Если 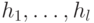 не порождают всю группу
не порождают всю группу  , то они содержатся в некоторой максимальной собственной подгруппе
, то они содержатся в некоторой максимальной собственной подгруппе 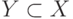 . Для каждого
. Для каждого  вероятность такого события не превосходит
вероятность такого события не превосходит 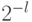 , поскольку
, поскольку  . Таким образом, мы имеем оценку
. Таким образом, мы имеем оценку
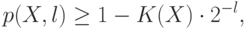
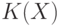 — число максимальных собственных подгрупп в группе
— число максимальных собственных подгрупп в группе  .
.Подгруппы абелевой группы  находятся во взаимнооднозначном соответствии с подгруппами группы характеров
находятся во взаимнооднозначном соответствии с подгруппами группы характеров 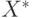 , при этом максимальным собственным подгруппам отвечают минимальные ненулевые подгруппы. Каждая такая подгруппа порождается одним элементом, поэтому
, при этом максимальным собственным подгруппам отвечают минимальные ненулевые подгруппы. Каждая такая подгруппа порождается одним элементом, поэтому  .
.
12.2 Построим классический оператор  (базисные векторы в
(базисные векторы в 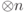 занумерованы от
занумерованы от  до
до  ), такой что
), такой что

![V^{-1}[0,B]\,U[B,A]\,V[0,B]](/sites/default/files/tex_cache/165d90b3e2c63873ee203e6ba1668999.png) реализует оператор
реализует оператор ![\Lambda(U_b)[0,A]](/sites/default/files/tex_cache/04b11c68cb56d9eb34ea672652f01d6f.png) в расширенном смысле.
в расширенном смысле.12.3 Обозначим образ вектора 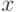 при преобразовании Фурье через
при преобразовании Фурье через 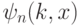 . В задаче 8.4 мы научились строить вектор
. В задаче 8.4 мы научились строить вектор 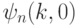 . Как уже отмечалось в решении задачи 7.11,
. Как уже отмечалось в решении задачи 7.11, 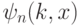 — собственный вектор классического оператора
— собственный вектор классического оператора  , собственное число которого равно
, собственное число которого равно  .
.
Используя эти соображения и результат задачи 11.2, построим следующую схему для квантового преобразования Фурье.
- В дополнительном, изначально нулевом, регистре построим вектор
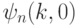 . Общее состояние получается
. Общее состояние получается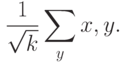
- Сделаем фазовый сдвиг на
 . Теперь получаем состояние
. Теперь получаем состояние 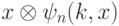 .
. - Измеряя обратимым образом (см. задачу 11.2) собственное число оператора
 , действующего на второй регистр, прибавляем результат измерения
, действующего на второй регистр, прибавляем результат измерения  к первому регистру. (Здесь имеется в виду побитовое сложение по модулю 2). В первом регистре получается
к первому регистру. (Здесь имеется в виду побитовое сложение по модулю 2). В первом регистре получается  , а во втором — требуемый результат
, а во втором — требуемый результат 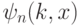 .
.
Из раздела 14
14.1 Оператор  можно представить в виде
можно представить в виде
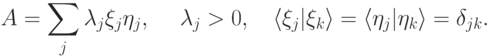
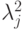 — ненулевые собственные числа оператора
— ненулевые собственные числа оператора  ,
,  — его собственные векторы, а
— его собственные векторы, а  . Тогда
. Тогда  .
.Для любого оператора 

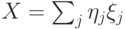 , то
, то 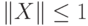 , а
, а 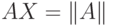 .
.Из доказанного представления для 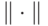 легко следует неравенство треугольника, а положительность и однородность
легко следует неравенство треугольника, а положительность и однородность 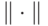 очевидны.
очевидны.
14.2 Свойство а):
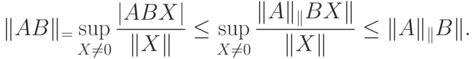
 ).
).Свойство в):
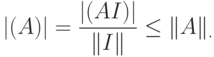
Свойство г): для любого 
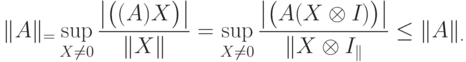
Свойство д):

14.3 Пусть  — пространство состояний q-битов из
— пространство состояний q-битов из  , а
, а  — пространство состояний остальных q-битов. Обозначим
— пространство состояний остальных q-битов. Обозначим
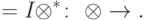
 , то
, то  . Следовательно, код
. Следовательно, код  исправляет ошибки из
исправляет ошибки из  .
.Преобразование 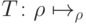 может быть разложено в операторную сумму (
может быть разложено в операторную сумму (  ), см. решение задачи 10.1. Операторы
), см. решение задачи 10.1. Операторы  из этого разложения принадлежат пространству
из этого разложения принадлежат пространству  , поэтому
, поэтому 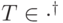 . Осталось воспользоваться теоремой 14.2.
. Осталось воспользоваться теоремой 14.2.
14.4 Пространство  , соответствующее искомому коду, порождается строками таблицы
, соответствующее искомому коду, порождается строками таблицы

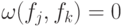 для любых двух строк
для любых двух строк 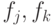 . Заметим, что столбцы в таблице разбиты на пары. Если взять любые две пары, то соответствующие 4 столбца линейно независимы. Следовательно, из строк всегда можно составить линейную комбинацию, которая в двух заданных парах позиций содержит заданные числа. Поэтому условия
. Заметим, что столбцы в таблице разбиты на пары. Если взять любые две пары, то соответствующие 4 столбца линейно независимы. Следовательно, из строк всегда можно составить линейную комбинацию, которая в двух заданных парах позиций содержит заданные числа. Поэтому условия 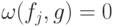 (
( 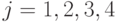 ) при
) при  могут выполняться только для
могут выполняться только для  .
.14.5 (См. [22, 23].) Допустим, что  — код типа
— код типа 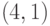 , исправляющий одну ошибку. Тогда он должен обнаруживать по крайней мере две ошибки, в частности, ошибки в q-битах
, исправляющий одну ошибку. Тогда он должен обнаруживать по крайней мере две ошибки, в частности, ошибки в q-битах ![[1,2]](/sites/default/files/tex_cache/f79408e5ca998cd53faf44af31e6eb45.png) , а также в q- битах
, а также в q- битах ![[3,4]](/sites/default/files/tex_cache/b814fa889082069ffb727ee1623c0944.png) . Это означает, что произвольное состояние
. Это означает, что произвольное состояние  можно восстановить как по первым, так и по последним двум
можно восстановить как по первым, так и по последним двум  -битам (см. задачу 14.3). Покажем, что это невозможно.
-битам (см. задачу 14.3). Покажем, что это невозможно.
Пусть  — пространство состояний q-битов
— пространство состояний q-битов ![[1,2]](/sites/default/files/tex_cache/f79408e5ca998cd53faf44af31e6eb45.png) , а
, а 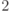 — пространство состояний q-битов
— пространство состояний q-битов ![[3,4]](/sites/default/files/tex_cache/b814fa889082069ffb727ee1623c0944.png) , тогда
, тогда  — это подпространство в
— это подпространство в  . Вложение
. Вложение 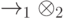 обозначим через
обозначим через  (это изометрический оператор). Пусть также
(это изометрический оператор). Пусть также 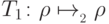 и
и 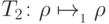 — преобразования ошибок, а
— преобразования ошибок, а 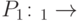 и
и 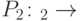 — соответствующие исправляющие преобразования. Тогда преобразование
— соответствующие исправляющие преобразования. Тогда преобразование  обладает следующим свойством: для любого
обладает следующим свойством: для любого 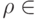
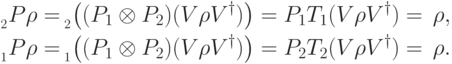
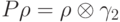 , где
, где 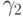 не зависит от
не зависит от  . Из второго тождества следует, что
. Из второго тождества следует, что 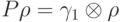 . Получили противоречие:
. Получили противоречие:  , где
, где  —любое.
—любое.14.6 Опишем кратко идею решения этой задачи.
Достаточно рассмотреть одно из двух прямых слагаемых торического кода. Компонента синдрома равна 1 для такого узла решетки, в звезду которого входит нечетное число ребер с ненулевыми весами в 1-цепи, соответствующей вектору ошибки 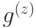 .
.
Поэтому получаем такую задачу. Задано некоторое множество  узлов решетки. Из всех 1-цепей
узлов решетки. Из всех 1-цепей  , граница которых совпадает с
, граница которых совпадает с  , нужно выбрать ту, в которой наименьшее число ребер ненулевого веса. Нетрудно сообразить, что такая 1-цепь распадается в объединение путей, соединяющих узлы из множества
, нужно выбрать ту, в которой наименьшее число ребер ненулевого веса. Нетрудно сообразить, что такая 1-цепь распадается в объединение путей, соединяющих узлы из множества  (любые два различных пути не имеют общих ребер), причем эти пути можно считать кратчайшими. Так что задача определения ошибки по синдрому сводится к задаче о взвешенном паросочетании: дан граф
(любые два различных пути не имеют общих ребер), причем эти пути можно считать кратчайшими. Так что задача определения ошибки по синдрому сводится к задаче о взвешенном паросочетании: дан граф  (в нашем случае полный), каждому его ребру приписан вес (в нашем случае — расстояние между узлами по решетке), нужно найти паросочетание, на котором достигается минимум суммы весов по ребрам, входящим в паросочетание.
(в нашем случае полный), каждому его ребру приписан вес (в нашем случае — расстояние между узлами по решетке), нужно найти паросочетание, на котором достигается минимум суммы весов по ребрам, входящим в паросочетание.
Для задачи о взвешенном паросочетании известны полиномиальные алгоритмы (см., например, [11, гл.11], где описан алгоритм, основанный на идеях линейного программирования).
