| Россия |
Спектрофотометрия в обратно рассеянном свете. Гемоглобиномеры и сенсоры кровенаполнения
19.2. Спектрофотометрия в обратно рассеянном свете
Рассмотрим теперь внимательнее трудности, связанные с переходом от классической схемы спектрофотометрического измерения "на просвет" к схеме измерений "на отражение". При последней схеме входной пучок света проникает сквозь кожу в живую ткань тела. Проходя сквозь ткань, свет рассеивается и поглощается. За счет рассеяния часть света возвращается к поверхности тела и выходит наружу. Спектральный состав света при этом изменяется в зависимости от наличия и от концентрации разных веществ в исследуемом участке тела. В отличие от схемы измерения "на просвет", путь, который проходит свет в живой ткани, при такой схеме измерения, вообще говоря, не фиксирован.
Для фотоплетизмографических сенсоров, оксиметров и пульсоксиметров это не играет особой роли. Но когда нужно измерять не относительную, а абсолютную концентрацию аналита, тогда путь  , который проходит свет в ткани, надо знать обязательно. Ибо, только зная этот путь, можно корректно вычислять концентрацию.
, который проходит свет в ткани, надо знать обязательно. Ибо, только зная этот путь, можно корректно вычислять концентрацию.
Возможно ли в принципе определить этот путь в схеме измерений "на отражение"? И, если возможно, то как именно? Этот вопрос и встал в 90-х г.г. ХХ в. перед исследователями и разработчиками спектрофотометрических интеллектуальных сенсоров.
19.2.1. Модель обратного рассеяния света
Точная математическая модель процесса распространения света в оптически сложной среде, которая не только поглощает и рассеивает свет, но еще и является такой неоднородной и многослойной, как биоткань вблизи поверхности человеческого тела, оказывается довольно сложной. Она не была столь разработана, чтобы из нее можно было сделать однозначные практические выводы.
Все более широкое применение в 70-80-х г.г. лазеров для диагностики и лечения разных заболеваний подтолкнуло физиков-оптиков детально изучить взаимодействие света с биологическими тканями. В этой области выполнено немало экспериментальных исследований (см., например, [
[
4
]
,
[
17
]
,
[
33
]
,
[
37
]
,
[
58
]
,
[
71
]
,
[
93
]
,
[
137
]
,
[
142
]
,
[
320
]
]). Экспериментально установлено, например, что средняя длина свободного пробега фотонов видимого света между рассеяниями в наружном (роговом) слое кожи человека составляет порядка 5 мкм, и при прохождении сквозь роговой слой свет рассеивается не больше 4  6 раз.
Средняя длина свободного пробега света в эпидермисе составляет уже примерно 20 мкм, и при прохождении сквозь эпидермис видимый свет рассеивается приблизительно 6
6 раз.
Средняя длина свободного пробега света в эпидермисе составляет уже примерно 20 мкм, и при прохождении сквозь эпидермис видимый свет рассеивается приблизительно 6  8 раз. В более глубоких слоях тела средняя длина свободного пробега фотонов видимого света между рассеяниями возрастает и составляет порядка 50 мкм. Следовательно, при прохождении сквозь тело пути в 2-4 мм свет рассеивается приблизительно 40-80 раз. В сумме имеем примерно 50-100 актов рассеяния. В этом случае нельзя применять такие упрощенные модели, как модель однократных рассеяний на большие углы, модель кратных рассеяний или диффузионную модель, которая "работает" при числе рассеяний свыше 500-1000. Наиболее приемлемой для данного случая является модель многократных рассеяний. Однако и она довольно сложна для подсчетов, которые обычно выполняются на ЭВМ методом статистического моделирования Монте-Карло.
8 раз. В более глубоких слоях тела средняя длина свободного пробега фотонов видимого света между рассеяниями возрастает и составляет порядка 50 мкм. Следовательно, при прохождении сквозь тело пути в 2-4 мм свет рассеивается приблизительно 40-80 раз. В сумме имеем примерно 50-100 актов рассеяния. В этом случае нельзя применять такие упрощенные модели, как модель однократных рассеяний на большие углы, модель кратных рассеяний или диффузионную модель, которая "работает" при числе рассеяний свыше 500-1000. Наиболее приемлемой для данного случая является модель многократных рассеяний. Однако и она довольно сложна для подсчетов, которые обычно выполняются на ЭВМ методом статистического моделирования Монте-Карло.
Из имеющихся экспериментальных данных и компьютерных расчетов вытекает, что интегральная интенсивность обратно рассеянного человеческим телом света может составлять от 5 до 30 % . Даже если свет входит в ткань перпендикулярно к поверхности кожи в виде узкого пучка, который можно назвать "световым зондом", то и в этом случае обратно рассеянный свет распределяется по довольно большой площади на поверхности ткани. Фотография на рис. 19.2 слева, сделанная на вертикальном разрезе матового стекла, в которое вводится "световой зонд", наглядно иллюстрирует характер распространения света в среде, рассеивающей свет. Справа показано диффузно размытое круглое пятно радиусом приблизительно 4-6 мм, которое наблюдается в обратно рассеянном сине-зеленом свете [ [ 257 ] ]. Снимок сделан цифровой фотокамерой сверху. Темную тень дает оптическое волокно, через которое в тело вводился "световой зонд".

Рис. 19.2. Фотография слева иллюстрирует характер распространения света в рассеивающей среде (матовое стекло); справа – фото обратно рассеянного от человеческой руки диффузно размытого пятна в сине-зеленом свете
19.2.2. Пучок наиболее вероятных траекторий света
В приближении геометрической оптики можно говорить о "траекториях" прохождения света в ткани. Обратное рассеяние света от тела теоретически может иметь место в результате нескольких его рассеяний на большие углы (см. рис. 19.3, а, где показано прохождение света в разрезе перпендикулярно к поверхности кожи).
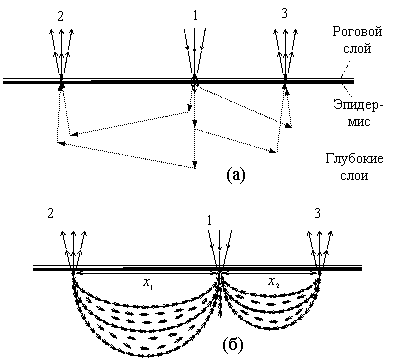
Рис. 19.3. а) Схематическое изображение обратного рассеяния светового пучка при нескольких рассеяниях на большие углы: 1 – первичный, 2 и 3 – обратно рассеянные световые пучки, отбираемые для измерений; б) пучки наиболее вероятных траекторий обратного рассеяния света посредством многократных рассеяний на малые углы
Кратчайший теоретически возможный путь света в ткани равняется при этом расстоянию х между точками входа и выхода света. Но для этого свет должен дважды (на входе и на выходе) рассеяться на большие углы. А вероятность рассеяния на большие углы намного меньше, чем вероятность рассеяния на малые углы. Поэтому такие траектории прохождения света в ткани являются наименее вероятными.
Более вероятными являются траектории прохождения света, обусловленные его многократными рассеяниями на малые углы ( рис. 19.3, б ). Пучок наиболее вероятных траекторий группируется вокруг траектории, близкой к дуге окружности, вдоль которой многократные рассеяния происходят на одинаковые наименьшие возможные углы. Такой пучок траекторий специалисты в шутку называют "бананом".
Если от входа в тело до выхода из него световой луч разворачивается на угол  , то такие наименьшие углы рассеяния составляют
, то такие наименьшие углы рассеяния составляют 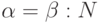 , где
, где  – суммарное число рассеяний. Если световой зонд входит в тело по нормали, и мы отбираем для измерений световой пучок, который выходит из тела тоже по нормали к его поверхности, то угол разворота составляет 180
– суммарное число рассеяний. Если световой зонд входит в тело по нормали, и мы отбираем для измерений световой пучок, который выходит из тела тоже по нормали к его поверхности, то угол разворота составляет 180  . Наименьшие углы рассеяния
. Наименьшие углы рассеяния 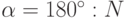 , что при
, что при 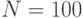 составляет
составляет 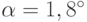 .
.
Таким образом, при использовании остро сфокусированного светового зонда с небольшим углом расхождения, при фиксированном направлении его входа в тело и при фиксированном направлении выхода измеряемого обратно рассеянного пучка света из тела среднестатистический путь  света в ткани является более или менее фиксированным и пропорциональным к
света в ткани является более или менее фиксированным и пропорциональным к  . (Расстояние х между входящим и выходящим пучками должно быть больше радиуса светового зонда – порядка 0,5 мм).
. (Расстояние х между входящим и выходящим пучками должно быть больше радиуса светового зонда – порядка 0,5 мм).
19.2.3. Характеристики светового поля обратного рассеяния света
Теоретические и экспериментальные исследования показали, что, когда "световой зонд" входит перпендикулярно к поверхности тела, то интенсивность обратно рассеянного света зависит от расстояния до точки облучения и от направления выхода. Световое поле, создаваемое обратно рассеянным от тела светом, можно детально охарактеризовать с помощью распределений интенсивности этого света по координатам и по направлениям выхода. В тех случаях, когда структура биоткани тела одинакова во всех направлениях от точки входа светового зонда, световое поле обратно рассеянного света является осесимметричным. И в этих случаях для описания распределений лучше всего использовать полярную систему координат.
Характер зависимости интенсивности обратно рассеянного света от расстояния до точки облучения для таких случаев приблизительно показан на
рис.
19.4. Здесь 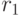 – радиус светового зонда,
– радиус светового зонда, 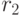 – расстояние, на котором интенсивность обратно рассеянного света становится максимальной. Положение максимума зависит от рассеивающих свойств биоткани, от поглощения света в ней, от спектрального состава света.
– расстояние, на котором интенсивность обратно рассеянного света становится максимальной. Положение максимума зависит от рассеивающих свойств биоткани, от поглощения света в ней, от спектрального состава света.
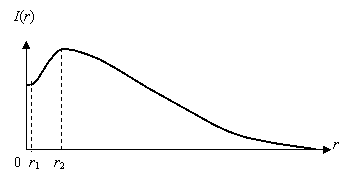
Рис. 19.4. Характер распределения интенсивности рассеянного света от расстояния до точки входа светового зонда
На рис. 19.5, например, показана экспериментально найденная зависимость от расстояния до точки облучения интенсивности зеленого света, обратно рассеянного мягкими тканями руки в направлении, перпендикулярном к поверхности кожи, [ [ 45 ] ]. Вдоль горизонтальной оси здесь отложено расстояние, по вертикальной оси – интенсивность света в относительных единицах. Интервалы между метками соответствуют расстояниям в 0,05 мм. Область в центре экранирована оптическим волокном с оболочкой, внутренний диаметр которого составляет 1 мм. Поэтому на расстояниях от центра, меньших 0,5 мм, отсчеты близки к нулю. Видно, что интенсивность света в этом случае после достижения максимума экспоненциально уменьшается с расстоянием в соответствии с законом Ламберта-Бэра (см. формулу 19.3).
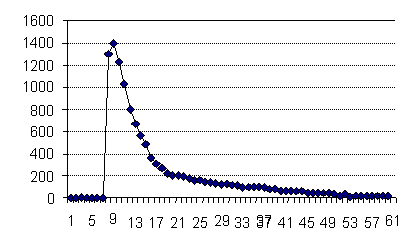
Рис. 19.5. Зависимость интенсивности обратно рассеянного зеленого света от расстояния до точки облучения
В каждой точке выхода из тела интенсивность обратно рассеянного света распределена по направлениям выхода. Каждое направление можно задать двумя углами: углом  между направлением выхода и нормалью к поверхности кожи и азимутальным углом
между направлением выхода и нормалью к поверхности кожи и азимутальным углом  , который отсчитывается от луча, проведенного от точки входа светового зонда к точке выхода света.
, который отсчитывается от луча, проведенного от точки входа светового зонда к точке выхода света.
Распределение интенсивности по углам  зависит от расстояния до точки входа светового зонда. Характер распределений в плоскости, проведенной через перпендикуляр к поверхности кожи и радиус-вектор точки выхода, показан на
рис.
19.6. Положительные углы отсчитываются от нормали в сторону радиус-вектора, проведенного в точку выхода от точки входа светового зонда.
зависит от расстояния до точки входа светового зонда. Характер распределений в плоскости, проведенной через перпендикуляр к поверхности кожи и радиус-вектор точки выхода, показан на
рис.
19.6. Положительные углы отсчитываются от нормали в сторону радиус-вектора, проведенного в точку выхода от точки входа светового зонда.

Рис. 19.6. Распределение обратно рассеянного света по углам theta: (а) недалеко от точки входа светового зонда; (б) на средних расстояниях; (в) на значительных расстояниях. Сверху – графики зависимости І( theta ), снизу – индикатриссы рассеяния
Рис. 19.6, а дает картину распределения по углам  вблизи от точки входа светового зонда,
рис.
19.6, б – на средних расстояниях, а
рис.
19.6, в – далеко от точки входа. Во всех случаях ( а, б, в ) сверху приведен график зависимости интенсивности обратно рассеянного света
вблизи от точки входа светового зонда,
рис.
19.6, б – на средних расстояниях, а
рис.
19.6, в – далеко от точки входа. Во всех случаях ( а, б, в ) сверху приведен график зависимости интенсивности обратно рассеянного света 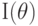 , а внизу – диаграмма (индикатрисса) рассеяния. Вблизи от точки входа света в тело картина распределения по углам
, а внизу – диаграмма (индикатрисса) рассеяния. Вблизи от точки входа света в тело картина распределения по углам  обычно асимметрична: интенсивность света, выходящего под положительными углами
обычно асимметрична: интенсивность света, выходящего под положительными углами  (т.е. от точки входа), значительно больше интенсивности света, выходящего под отрицательными углами.
Максимум углового распределения интенсивности смещен в сторону положительных углов
(т.е. от точки входа), значительно больше интенсивности света, выходящего под отрицательными углами.
Максимум углового распределения интенсивности смещен в сторону положительных углов  . Далеко от точки входа распределение обратно рассеянного света по углам
. Далеко от точки входа распределение обратно рассеянного света по углам  приближается к равномерному, а максимум находится вблизи нормали к поверхности. На средних расстояниях имеет место промежуточная асимметрия.
приближается к равномерному, а максимум находится вблизи нормали к поверхности. На средних расстояниях имеет место промежуточная асимметрия.
Характер распределения интенсивности обратно рассеянного телом света по азимуту показан на
рис.
19.7. На
рис.
19.7, а показана проекция направления обратно рассеянного света на плоскость поверхности тела. Проекция обозначена буквой  . Там же показано, как отсчитывается азимут
. Там же показано, как отсчитывается азимут  . Типичный вид распределения по азимуту на небольших расстояниях от точки входа света показан на
рис.
19.7, б. Распределение является неравномерным. Интенсивность света, выходящего из тела в направлении от точки входа света, – наибольшая, а выходящего в обратном направлении, – наименьшая.
Типичное распределение интенсивности обратно рассеянного света по азимуту на больших расстояниях от точки входа показано на
рис.
19.7, в. Оно приближается к равномерному. На
рис.
19.7, б и в сверху приведены графики зависимости
. Типичный вид распределения по азимуту на небольших расстояниях от точки входа света показан на
рис.
19.7, б. Распределение является неравномерным. Интенсивность света, выходящего из тела в направлении от точки входа света, – наибольшая, а выходящего в обратном направлении, – наименьшая.
Типичное распределение интенсивности обратно рассеянного света по азимуту на больших расстояниях от точки входа показано на
рис.
19.7, в. Оно приближается к равномерному. На
рис.
19.7, б и в сверху приведены графики зависимости 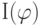 , а внизу – диаграммы (индикатриссы) рассеяния.
, а внизу – диаграммы (индикатриссы) рассеяния.
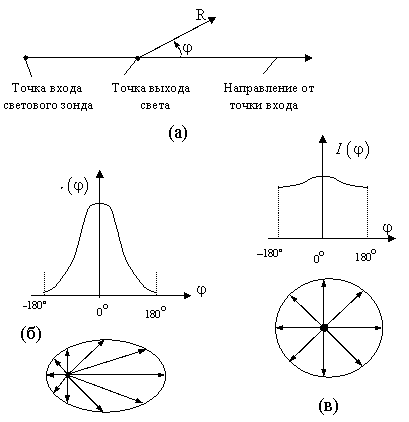
Рис. 19.7. Характер распределения интенсивности обратно рассеянного телом света по азимутальным углам: (а) схема отсчета азимута; (б) распределение вблизи от точки входа; (в) распределение далеко от точки входа
На небольших и средних расстояниях от точки входа светового зонда в принципе для каждой точки поверхности тела и каждого направления выхода света из тела можно указать пучок наиболее вероятных траекторий прохождения света внутри тела и определить среднестатистическую длину траектории. На больших расстояниях от точки входа зонда пучок наиболее вероятных траекторий уже трудно выделить, а дисперсия их длины уже приближается к самой длине. Поэтому на больших расстояниях от точки зондирования тела путь, пройденный в теле обратно рассеянным светом, становится неопределенным. Такие расстояния непригодны для спектрофотометрии в обратно рассеянном свете.
19.2.4. Технология измерений в обратно рассеянном свете
Из описанной модели обратного рассеяния света человеческим телом, вытекающей из теоретических и экспериментальных исследований, стало ясным, что спектрофотометрические исследования и измерения при работе "на отражение" возможны при выполнении четырёх важных условий:
- Зондирующий световой пучок должен входить в исследуемый участок тела в виде остро направленного светового "зонда".
- Направление светового зонда должно быть фиксировано конструкцией сенсора. (Обычно пучок света перпендикулярен к поверхности тела).
- Для измерения спектральных интенсивностей следует выделять пучок обратно рассеянного света, выходящий на определенном расстоянии от точки входа светового зонда и в строго определенном направлении.
- Точка отбора измеряемого пучка обратно рассеянного света должна находиться на средних расстояниях от точки зондирования (1-5 мм), когда обратно рассеянный свет не стал еще "диффузным" (равномерно распределенным по всем направлениям).
Только при этих условиях можно говорить о пучке наиболее вероятных траекторий прохождения света и о среднестатистическом пути, пройденном обратно рассеянным светом в исследуемом участке тела.
В конструкции сенсора эти условия проще всего реализовать, используя оптические волокна с небольшой угловой апертурой. По одним из них, входящим в оптический контакт с телом, в исследуемый участок тела вводится световой зонд. А с помощью других, расположенных на заданном расстоянии от точки входа светового зонда и тоже имеющих оптический контакт с телом, отбираются для измерений только те обратно рассеянные световые лучи, которые выходят из тела в заданном направлении.
Надежный оптический контакт между телом и оптическими волокнами, из которых вводится световой зонд и отбирается для анализа нужная часть обратно рассеянного света, можно обеспечить, размещая между оптической головкой и телом тонкий слой иммерсионной жидкости с показателем преломления, близким к эффективному показателю преломления кожи. Если эта жидкость еще и поверхностно активна, то она заполняет все поры, которые всегда имеются в коже, и тем самым заметно уменьшает чисто поверхностное рассеяние света, увеличивая глубину его проникновения в тело. Такой иммерсионной жидкостью в простейшем случае могут быть обычная вода, физиологический раствор, глицерин. В работе [ [ 136 ] ] предлагается применять глицерол (смесь глицерина с крахмалом).

