| Россия |
Проектирование и инженерия алгоритма: топологическая сортировка
10.5. Уроки
Из алгоритма топологической сортировки можно вывести важные следствия, общезначимые для проектирования алгоритмов и для программной инженерии в целом.
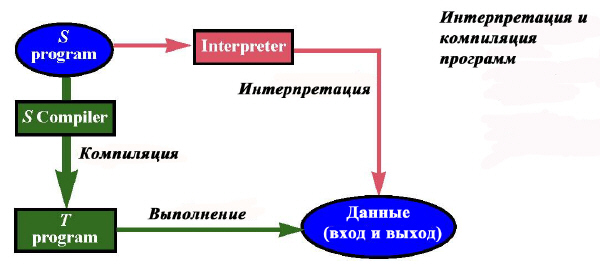
Интерпретация в сравнении с компиляцией
Мы уже рассматривали два стиля выполнения программ, написанных на некотором языке программирования S.
- Интерпретация. Написать программу, называемую Интерпретатором, которая может выполнять произвольную S-программу для произвольных входных данных.
- Компиляция. Написать программу, называемую Компилятором, которая может преобразовать произвольную S-программу в программу с эквивалентной семантикой, записанную на целевом языке T. Если T – это машинный язык для применяемой платформы, то результат компиляции может быть непосредственно выполнен. В противном случае T-программа может быть интерпретирована или подвергнута дальнейшей компиляции.
Как отмечалось, практическая реализация языков часто комбинирует оба подхода.
Эти концепции обобщаются на многие проблемные области, отличающиеся от выполнения программ, которые написаны на языках высокого уровня. Для выполнения некоторой обработки на некотором входе мы можем использовать структуры данных, которые непосредственно отображают вход, или можем разбить процесс обработки на два этапа.
- Компиляция: преобразовать данные в форму, более подходящую для целей алгоритма.
- Интерпретация: применять требуемые операции к исходной структуре данных.
Этот прием (который, как и при обработке языков, может и в общем случае включать несколько итераций процесса) в точности был применен для топологической сортировки. Вначале мы рассмотрели интерпретационное решение, которое использует кажущиеся естественными структуры данных, непосредственно следуемые из постановки задачи. Но оказалось, что эти структуры приводят к "плохому" по производительности решению. "Компиляция" их в представление, подогнанное под наши цели, привело к решению с прекрасной производительностью.
В таком двухэтапном решении шаг "компиляции", инициализирующий структуры данных, может быть столь же сложным для проектирования, как и фактическая обработка, основанная на этих структурах, – он может требовать столь же много времени, а иногда и больше, чем время самой обработки. Этот подход хорош, если общая производительность соответствует вашим целям, но, конечно же, нельзя перепрыгивать к заключению о производительности алгоритма, не учитывая время инициализации, а не только самой обработки.
Подход может быть обобщен в виде эвристики – универсальной стратегии, подобной "образцу проектирования", но в существенно более абстрактной форме.
Почувствуй эвристику
Хорошие алгоритмы часто создаются с использованием двухэтапной стратегии, где:
- на первом этапе преобразуется вход из его исходной формы во внутренние структуры, тщательно спроектированные и подогнанные под цели задачи;
- на втором шаге обрабатываются преобразованные данные для получения конечного результата.
Мы увидим еще одно применение этой идеи при обсуждении архитектуры процесса проектирования, управляемого событиями.
Компромисс "время-память"
Выбора тяжко бремя – память иль время!
Тесно связанным с эвристикой "Вначале компилируй данные" является наблюдение, что идеальная структура данных, та, которая наилучшим способом помогает реализации второго шага, часто не является наиболее экономичным по памяти представлением информации. В топологической сортировке информация об ограничениях может сохраняться в трех различных частях. Ограничение [x, y] ведет к тому, что y появится также в списке последователей x в массиве successors; некоторая информация хранится в массиве predecessor_count[y]. Если для заданного y ограничения отсутствуют, то это приводит к добавлению элемента в массив candidates. При таком представлении нам приходится жертвовать памятью для достижения требуемой по времени производительности. Компромиссы такого вида в ту или иную сторону – ключевые моменты проектирования эффективных алгоритмов.
Алгоритмы в сравнении с программами и компонентами
Вполне возможно было бы привести описание алгоритма топологической сортировки, которое игнорирует многие из аспектов, рассмотренных в этой лекции, концентрируясь только на процессе сортировки. Для практического решения необходимо принимать в расчет практические потребности приложений. ОО-подход позволяет нам действовать в соответствии с этими целями. Вместо написания процедуры топологической сортировки мы проектируем класс TOPOLOGICAL_SORTER. Экземпляр этого класса характеризует задачу топологической сортировки, предоставляя не только алгоритм ее решения (процедуру process), но и весь инструментарий, необходимый клиенту для того, чтобы он мог:
- поставить задачу, записав элементы и ограничения удобным для себя способом;
- применить process для выполнения топологической сортировки заданных элементов, удовлетворяющих заданным ограничениям;
- запросить данные о результирующем состоянии, выяснить, существуют ли циклы, и если да, то получить информацию об элементах, входящих в цикл.
Разница между этим подходом и чистым алгоритмом является частью разницы между программной инженерией и чистым программированием. В инженерии программ недостаточно спроектировать умный алгоритм и связанные с ним структуры данных. Целью становится подготовка решения, которое может быть интегрировано в успешные программные системы.
Наши решения должны допускать повторное использование, так что они не просто представляют "образцы проектирования", которые программист может интегрировать в свою систему, купив и прочитав книги (особенно выдающиеся книги, такие как эта, например). Решения должны быть реализованы как компоненты, доступные всегда и для всех, непосредственно доступные, а не стоящие на полках.
Вы также обратили внимание на то, как в этом процессе контракты позволяют нам точно знать, что нам следует делать, – что мы ожидаем, что гарантируется и что мы поддерживаем.
10.6. Ключевые концепции этой лекции
- Топологическая сортировка является перечислением множества элементов, которое совместимо с множеством ограничений порядка, заданного на этих элементах.
- Задача имеет простое математическое описание: задано (строгое) отношение порядка, требуется найти полное отношение, чьим подмножеством является исходное отношение.
- На практике отношение обычно является не отношением порядка, а в лучшем случае ациклическим отношением. Взятие транзитивного замыкания дает отношение порядка.
- Реалистичное, хорошее инженерное решение должно принимать, возможно, ошибочный вход, содержащий циклы. Оно должно выполнять топологическую сортировку ацикличной части исходного отношения и дополнительно выдать информацию об элементах, входящих в цикл.
- Такое решение должно предоставлять не только алгоритм топологической сортировки, но и механизмы построения экземпляра задачи с вводом элементов и ограничений.
- Для n элементов и m ограничений топологическую сортировку можно выполнить за O(m + n) время, используя память того же порядка.
- Ключом эффективности алгоритма является построение структур данных, специально приспособленных для решения задачи сортировки:
- массив, который для каждого элемента исходного множества содержит список его последователей;
- массив, который для каждого элемента исходного множества содержит число его предшественников;
- распределитель (стек, список или очередь с приоритетами), который содержит множество элементов, не имеющих предшественников.
- На примере задачи сортировки показано, что хорошее алгоритмическое решение часто получается путем "компиляции" исходных данных задачи в специально спроектированные структуры данных, которые затем могут быть эффективно "интерпретируемы".
Новый словарь
10.7. Приложение. Терминологические замечания об отношениях порядка
Для обсуждения топологической сортировки удобно – как показано в этой лекции – использовать отношение строгого порядка: "строго меньше, чем". Классическим примером такого отношения является отношение "<", заданное на числах. В некоторых задачах может быть более полезным иметь дело с нестрогим отношением, как отношение "<=" для чисел. Пара элементов связана нестрогим отношением x <= y, если и только если либо x < y, либо x = y. Общепринятое соглашение для "отношения порядка" предполагает нестрогую версию. В этой главе, так как мы использовали только строгое отношение порядка, слово "строгое" обычно опускалось, так что "порядок" означал "строгий порядок".
Для отношения строгого порядка (иррефлексивного и транзитивного) в литературе иногда используется термин "квазипорядок". Конечно, каждый может дать любое имя понятию, задав его точное определение, но это конкретное имя неудачно, так как ничего "квази" в таком порядке нет. Если и есть что-нибудь характерное для элементов в этом порядке, то это то, что они "более" упорядочены, чем для случая нестрогого порядка, поскольку имеет место иррефлексивность, запрещающая элементу находиться в отношении с самим собой. Чтобы совсем запутать дело, некоторые авторы используют термин "квазипорядок" для отношений, которые являются рефлексивными и транзитивными. Так что лучше этот термин "квази" не использовать и вместо этого квалифицировать отношение порядка как "строгое", когда это необходимо.
Еще одна проблема: является ли отношение тотальным или нет. Тотальность означает, что для любых пар различных элементов x и y имеет место одно из двух – либо x < y, либо y < x. Отношение порядка, удовлетворяющее этому свойству, называется тотальным порядком. Частичным порядком должно было бы называться отношение, которое не удовлетворяет этому свойству, такое, что для него найдется по крайней мере одна пара различных элементов, для которой ни [x, y], ни [y, x] не принадлежат отношению. Но не так определяется частичный порядок в большинстве литературных источников – там частичный порядок определяется как такой порядок, о котором неизвестно, является ли он тотальным. Другими словами, это отношение возможно частичного порядка. Это приводит к путанице, так как теперь тотальный порядок является также частичным порядком! Поэтому лучше писать так, как принято в этой лекции:
- тотальный порядок – в тех случаях, когда известно, что он тотальный;
- частичный порядок – для отношения порядка, о котором известно, что порядок не является тотальным.
Если же мы не знаем, каков порядок, или хотим включить оба случая – лучше применять термин "порядок". В случае неопределенности –использовать термин "возможно частичный порядок".
10.8. Упражнения
10.8.1. Словарь
Дайте точные определения символам словаря.
10.8.2. Иррефлексивность и асимметричность
Отношение порядка было определено как транзитивное и иррефлексивное. Было доказано, что следствием является асимметричность отношения. Докажите, что если отношение определяется как транзитивное и асимметричное, то следствием является иррефлексивность.
10.8.3. Тотальный порядок и перечисление
Докажите, что если отношение r является отношением строгого тотального порядка на конечном множестве, то существует единственное перечисление элементов, такое, что для любых элементов x и y элемент x появится перед y в перечислении, если и только если пара [x, y] принадлежит r.
10.8.4. Строгое отношение в сравнении с нестрогим отношением порядка
Обсуждение в этой лекции строилось на строгом отношении порядка (частичном или полном), таком, как отношение "<" на числах – "меньше чем". Также возможно использовать нестрогое отношение порядка, такое, как "≤" – "меньше или равно". Определение строгого частичного порядка, которое мы будем называть отношением "<", хотя оно и не должно быть обычным отношением на числах, должно удовлетворять свойствам:
| О1 | иррефлексивности: | x < x не выполняется для любого x. |
| О2 | транзитивности: | из того, что x < y и y < z, следует x < z. |
Для этого отношения также выполняется свойство:
Свойство О3 является следствием двух предыдущих свойств. Для частичного нестрогого отношения порядка "≤" имеют место три независимых свойства:
| N1 | рефлексивности: | x≤x для любого x. |
| N2 | транзитивности: | из того, что x≤y и y≤z, следует x≤z. |
| N3 | антисимметричности: | из того, что x≤y и y≤x, следует x = y. |
Для любого частичного строгого отношения порядка "<" существует связанное с ним нестрогое отношение "≤", определенное как
x ≤ y если и только если: x < y или x = y [4]
Пример
10.4.
Справедливо и обратное утверждение: для любого частичного строгого отношения порядка "≤" существует связанное с ним строгое отношение "<", определенное как
x < y если и только если: x ≤ y и x ≠ y [5]
Пример
10.5.
В этом упражнении требуется исследовать связь между этими ассоциированными отношениями – строгим "<" и нестрогим "≤"
- Докажите, что если "<" является частичным строгим отношением порядка, то "≤", определенное в примере 10.4, является частичным нестрогим отношением порядка.
- Докажите, что если "≤" является частичным нестрогим отношением порядка, то "<", определенное в примере 10.5, является частичным строгим отношением порядка.
- В строгом случае определение требует выполнения только двух свойств: иррефлексивности и транзитивности. Третье свойство асимметричности является следствием двух остальных. В нестрогом случае требуется выполнение всех трех свойств. Докажите, что антисимметричность не является следствием двух остальных. Другими словами, приведите пример нестрогого отношения, для которого первые два свойства выполняются, а антисимметричность не имеет места.
- Докажите, что замена "рефлексивности" на "иррефлексивность" в определении нестрогого порядка приводит к определению строгого порядка.
- Приводит ли замена "иррефлексивности" на "рефлексивность" в определении строгого порядка к определению нестрогого порядка?
10.8.5. Ацикличность и отношение тотального порядка
Докажите теорему о топологической сортировке, используя вторую теорему об ацикличности и отношениях порядка.
10.8.6. Интересное постусловие
Объясните постусловие функции has_element.
10.8.7. Оптимизация использования хэш-таблицы
В процедуре record_element проверяется, присутствует ли уже вставляемый элемент в таблице index_of_element, и запись осуществляется только в случае, когда такого элемента нет. В реализации используются две операции поиска – одна при вызове has_element, другая при вызове extend. Проанализируйте контрактную форму класса HASH_TABLE, найдите нужные компоненты, перепишите процедуры так, чтобы устранить эту небольшую неэффективность.
10.8.8. Программирование топологической сортировки
Постройте класс TOPOLOGICAL_SORTER в соответствии с обсуждением этой лекции.
10.8.9. Параметризация топологической сортировки
(Это упражнение предполагает, что выполнено предыдущее)
Расширьте реализацию топологической сортировки, позволяя клиентам задавать стратегию выбора элемента из множества соревнующихся "кандидатов".