| Россия |
Проектирование и инженерия алгоритма: топологическая сортировка
Одна из тех радостей, что доставляет нам изучение информатики, – это знакомство с замечательными алгоритмами. В этой лекции мы займемся исследованием алгоритма, который обладает рядом достоинств, заслуживающих нашего внимания. Он полезен на практике, он, обладая хорошим математическим базисом, элегантен, он иллюстрирует технику решения задач, применимую в различных контекстах.
Познакомить вас с уже готовым решением неинтересно. Вместо этого мы начнем разрабатывать это решение шаг за шагом, как это делается для всякой научной проблемы. Мы начнем с постановки задачи, перейдем к ее математическому анализу, займемся поиском структуры данных, обеспечивающих корректность и эффективность решения. Мы не только спроектируем алгоритм, но, не останавливаясь на этом, получим полное инженерное решение, удовлетворяющее всем практическим требованиям. В конце лекции уроки этого примера позволят сформулировать некоторые общие принципы разработки алгоритмов и инженерии программ.
10.1. Постановка задачи
Вы решили сегодняшний день посвятить культуре: что может быть лучше, чем посещение Лувра и музея Орсе в Париже? Но для этого вам понадобится карта, и нужно приобрести проездной на метро, поскольку срок старого уже истек, но для проездного нужны деньги, так что придется зайти в банк или воспользоваться банкоматом. Можно выразить эти ограничения следующим образом:
[Map, Louvre], [Map, Orsay], [Pass, Louvre], [Pass, Orsay], [Money, Pass]
Здесь каждое ограничение задается парой [x, y], означающей, что "x должно случиться прежде чем y". Это можно отобразить графически:
Топологической сортировкой множества элементов, подчиняющихся ограничениям порядка, называется перечисление элементов в порядке, удовлетворяющем ограничениям. В данном примере топологическими сортировками являются последовательности:
Money, Pass, Map, Louvre, Orsay
Map, Money, Pass, Orsay, Louvre
Money, Map, Pass, Louvre, Orsay
Заметьте: последовательность Pass, Money, Map, Louvre, Orsay некорректна, поскольку нарушается ограничение [Money, Pass].
Задача топологической сортировки может иметь:
- несколько решений, как в данном примере;
- в точности одно решение;
- ни одного решения, как было бы, в случае если и только если ограничения образовывали бы цикл – множество ограничений:
![[e_1,e_2], [e_2, e_3], \ldots [e_n, e_1]](/sites/default/files/tex_cache/79eb6304a200d7d3a67a0a22f40f92ba.png) для некоторого
для некоторого  . Если мы добавим в наш пример ограничение [Orsay, Money], создавая тем самым цикл, то никакого решения больше существовать не будет, так как мы, с одной стороны, требуем, чтобы "утром – стулья, вечером – деньги", а с другой стороны, требуем "деньги вперед".
. Если мы добавим в наш пример ограничение [Orsay, Money], создавая тем самым цикл, то никакого решения больше существовать не будет, так как мы, с одной стороны, требуем, чтобы "утром – стулья, вечером – деньги", а с другой стороны, требуем "деньги вперед".
Если существует более одного решения, то возникает проблема выбора одного из них. Обычно с любым решением связывается некоторая стоимость, тогда целью может быть поиск решения с минимальной стоимостью. Вскоре при анализе алгоритма мы увидим, где может применяться этот критерий при поиске нужного решения. Другой подход может состоять в том, чтобы найти все решения.
Примеры применения
Задача топологической сортировки возникает всякий раз, когда требуется упорядочить элементы при некоторых ограничениях на их порядок следования. Вот несколько примеров.
- Для графического дисплея рассмотрим окна – графические прямоугольники, которые могут пересекаться. Нам необходим алгоритм, рисующий эти прямоугольники с учетом их наложения друг на друга. Это задача топологической сортировки. Зададим следующие ограничения: [B, A], [D, A], [D, C], [B, D], [E, C]. Здесь ограничение [x, y] содержательно означает "x не должно скрывать никакую часть y". Возможным решением является последовательность: B, D, E, A, C.
- При промышленной сборке сложных изделий – турбины или самолета – множество задач по управлению сборкой сопровождается ограничениями, например, структурная работа над элементом должна предшествовать его окраске. Топологическая сортировка дает расписание, совместимое с этими ограничениями.
- Подобная задача возникает при управлении проектами, особенно при управлении программными проектами. Если проект связан с некоторой проблемной областью, то он должен сопровождаться глоссарием (словарем) технических терминов (непонимание между экспертами проблемной области и разработчиками ПО является главным источником ошибок и провалов). Определение любого термина может ссылаться на другие термины. Термины в словаре могут идти в алфавитном порядке, как принято в словарях, но также полезно иметь версию словаря, которая может читаться в последовательности, где каждый термин объясняется через уже определенные термины. Создание такого словаря предполагает топологическую сортировку.
- При описании класса вы, возможно, хотели бы, чтобы его компоненты шли в порядке, гарантирующем, что никакой вызов компонента не встречается до его описания1В некоторых языках программирования таково требование синтаксиса. Но взаимная рекурсия методов, когда А вызывает В, а В вызывает А, приводит к циклу, так что в язык приходится вводить специальные конструкции предварительного объявления (предварительно объявляется В, затем объявляется А, затем дается полное объявление В). .
- Топологическая сортировка позволяет улучшить эффективность компиляции ОО-программ при реализации наследования и в особенности – динамического связывания, обсуждаемого в последующих лекциях. Проблема актуальна для больших программ со многими классами и состоит в нумерации классов таким образом, чтобы номер, приписанный классу, был близок к номерам классов, являющихся его потомками – классами, которые наследуют от него прямо или косвенно. Используя "наследует от" как отношение порядка, компилятор EiffelStudio, основываясь на топологической сортировке, достигает существенной оптимизации требуемой памяти, что является основой жизнеспособности ОО-подхода.
Точки на плоскости
Вот пример, дающий удобную визуализацию задачи. Рассмотрим точки на плоскости:
Введем для точек 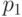 с координатами
с координатами 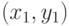 и
и 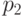 с координатами
с координатами 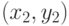 отношение
отношение  ("строго меньше"), устанавливающее, что
("строго меньше"), устанавливающее, что  , если:
, если:
-
 ;
; -
 ;
; -
 (точки не совпадают).
(точки не совпадают).
Для четырех точек, показанных на рисунке, справедливо следующее:

Топологическая сортировка для этого отношения дает любое перечисление точек, для которого если p « q, то в списке перечисления p предшествует q. Для наших четырех точек существуют три таких перечисления:
a, b, c, d
a, c, b, d
c, a, b, d
Три возможных обхода точек можно визуализировать:
С другой стороны, перечисление a, d, b, c не совместимо с отношением, поскольку свойство c « d требует, чтобы c предшествовало d.
10.2. Основы топологической сортировки
Задача, обсуждаемая в этой главе, имеет точную математическую формулировку.
Определение: задача топологической сортировки
Это определение использует математические понятия – отношения как множества, ациклические отношения, отношения порядка (полного или частичного), которые теперь предстоит рассмотреть.
Бинарные отношения
Определение: отношение
Примером отношения на множестве {1, 2, 3} является:
{[1, 2], [1, 3], [2, 3]}
Мы можем назвать это отношением < ("меньше", так как x и y принадлежат множеству {1, 2, 3} и x меньше y).
Мы можем использовать отношения для описания предыдущих примеров.
- Отношение below (ниже) на множестве прямоугольников, содержащее все пары прямоугольников [x, y], таких, что в области наложения прямоугольников должны показываться точки y, а не x.
- Отношение before (прежде) – множество пар {[Map, Louvre], [Map, Orsey], …} – является отношением на множестве {Pass, Money, Map, Louvre, Orsay}, содержащим пары [x, y], такие, что событие x должно произойти раньше y.
- Отношение used_in ("используется в"), заданное на множестве терминов словаря, содержит все пары [x, y], такие, что определение термина y содержит термин x.
- Отношение called_by ("вызывается в"), заданное на множестве методов класса, содержит все пары [x, y], такие, что тело метода y содержит вызов метода x.
- Отношение « над точками – множество пар {[a, b], [a, d], [b, d], [c, d]}.
Ациклические отношения
Все наши примеры были до сих пор ациклическими отношениями. Это понятие определяется следующим образом:
Определение: ациклическое отношение
Это определение следует дополнить.
Определение: цикл в отношении
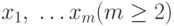 из элементов
из элементов  , такая, что все последовательные пары
, такая, что все последовательные пары ![[x_i,x_{i+1}]](/sites/default/files/tex_cache/ed75161bcea8dc1b8e616c48806cc6e7.png) для
для  принадлежат
принадлежат  , и
, и  .
.Отношение before, введенное ранее, циклов не имеет:
Для успеха топологической сортировки требуется ациклическое отношение, хотя мы будем рассматривать алгоритм, который может частично обрабатывать отношение, включающее цикл. Если множество, на котором определено отношение, конечно, то ациклическое отношение имеет важное свойство, критичное для алгоритма топологической сортировки.
Теорема об отсутствии предшественника
Определение: предшественник
Теорема доказывается от противного. Предположим противное, что каждый элемент в  имеет по меньшей мере одного предшественника. Пусть
имеет по меньшей мере одного предшественника. Пусть  – элемент из
– элемент из  (он существует, так как множество не пусто). По предположению, у него есть хоть один предшественник, выберем любой и назовем его
(он существует, так как множество не пусто). По предположению, у него есть хоть один предшественник, выберем любой и назовем его  . По тем же причинам есть предшественник
. По тем же причинам есть предшественник  и у
и у  , так что в
, так что в  существует пара
существует пара ![[x_3, x_2]](/sites/default/files/tex_cache/4550d01de6e3db08e52dac2803722a3a.png) . Продолжая вывод, следует признать существование бесконечной последовательности
. Продолжая вывод, следует признать существование бесконечной последовательности ![[x_{i+1}, x_i]](/sites/default/files/tex_cache/1ed81d959ef29b845ba0052ad421d551.png) , принадлежащей
, принадлежащей  для каждого
для каждого 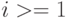 . Поскольку
. Поскольку  – конечное множество, последовательность должна иметь повторяющиеся элементы.
Более точно: у последовательности
– конечное множество, последовательность должна иметь повторяющиеся элементы.
Более точно: у последовательности  , где
, где  – число элементов
– число элементов  , все элементы не могут быть различными; поэтому должны быть целые
, все элементы не могут быть различными; поэтому должны быть целые  и
и  , для
, для  , такие, что
, такие, что  , но тогда последовательность
, но тогда последовательность  является циклом. Пришли к противоречию.
является циклом. Пришли к противоречию.
Доказательство конструктивно, и мы будем его использовать при проектировании алгоритма топологической сортировки. Для выработки перечисления алгоритм будет выискивать на каждой итерации элемент, не имеющий предшественника в оставшемся отношении порядка.
Предположение о конечности множества  существенно. Теорема неприменима к бесконечным множествам, например, отношение "меньше" для целых чисел в математике ациклическое, но каждый его элемент имеет предшественника.
существенно. Теорема неприменима к бесконечным множествам, например, отношение "меньше" для целых чисел в математике ациклическое, но каждый его элемент имеет предшественника.
Отношения порядка
Идея топологической сортировки встраивает данное ациклическое отношение в отношение полного (тотального) порядка. Для определения этого понятия предварительно определим простое отношение порядка.
Определение: отношение порядка (строгое, возможно частичное)
Такое отношение порядка является также:
| О3 | асимметричным: из того, что отношению принадлежит пара [x, y] следует, что отношению не принадлежит пара [y, x]. |
(Доказательство. Если бы обе пары принадлежали отношению, то из транзитивности следовала бы рефлексивность – существование пары [x, x], что противоречит свойству антирефлексивности)
Отношение "<" на {1, 2, 3} (или на любом другом множестве целых) является отношением порядка. Таким же является отношение « на точках. Наши другие ациклические отношения – before для задач, used_in для терминов, called_by для методов – антирефлексивны и асимметричны, но они не обязательно транзитивны, так что они не являются отношениями порядка. Вскоре мы увидим, как можно получить транзитивную версию.
Отношения порядка в сравнении с ациклическими отношениями
Отношения порядка тесно связаны с ациклическими отношениями. В одном направлении эта связь – прямая.
Теорема: "Ацикличность и отношение порядка" (1)
Доказательство от противного. Предположим, существует цикл  , где
, где 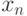 то же, что и
то же, что и  . По транзитивности это влечет рефлексивность, что противоречит антирефлексивности.
. По транзитивности это влечет рефлексивность, что противоречит антирефлексивности.
Здесь еще одно интересное свойство: транзитивное замыкание ациклического отношения является отношением порядка. Неформально транзитивное замыкание отношения представляет собой отношение порядка, полученное применением свойства транзитивности с помощью расширения исходного отношения настолько, насколько это возможно.
Это может быть проиллюстрировано на отношении before, выражающего ограничения порядка между задачами. Отношение антирефлексивно, асимметрично и ациклично, но оно не транзитивно, поскольку содержит пары [Money, Pass] и [Pass, Louvre], но не содержит пары [Money, Louvre]. Мы можем расширить отношение до транзитивного, добавив все пары вида [x, z], для которых в исходном отношении есть пары [x, y] и [y, z], выполняя эту операцию, пока добавление не перестанет быть возможным. Результатом этого процесса является транзитивное замыкание исходного отношения. Для нашего примера добавятся ровно две связи:
Для отношения called_by между процедурами транзитивное замыкание является отношением, которое выполняется между x и y, если у вызывает x прямо или косвенно. Для отношения child между людьми, обозначающего множество пар [x, y], таких, что x является потомком y, транзитивное замыкание служит отношением, связывающим двух людей, таких, что один из них является потомком, непосредственным или косвенным – прапраправнуком. Транзитивное замыкание отношения r обозначается как  , так что мы можем полагать, что
, так что мы можем полагать, что  (потомок представляет транзитивное замыкание отношения "потомок").
(потомок представляет транзитивное замыкание отношения "потомок").
Определение: транзитивное замыкание отношения
 на множестве
на множестве  является отношение, содержащее все пары вида
является отношение, содержащее все пары вида ![[x_1, x_m]](/sites/default/files/tex_cache/8dde4a45ae398cdb77859751b0640ac4.png) для некоторой последовательности элементов
для некоторой последовательности элементов  , такой, что пары
, такой, что пары ![[x_i, x_{i+1}]](/sites/default/files/tex_cache/b9ecd49b3245fff5c8a6ccb8e4a645be.png) для
для  принадлежат
принадлежат  .
.Транзитивное замыкание высвечивает другую сторону отношения между ацикличностью и порядком.
Теорема: "Ацикличность и отношение порядка" (2)
Доказательство. Транзитивное замыкание любого отношения  очевидно транзитивно. Так что нам остается доказать антирефлексивность. Предположим, что это не так и существует элемент
очевидно транзитивно. Так что нам остается доказать антирефлексивность. Предположим, что это не так и существует элемент  , такой, что пара
, такой, что пара ![[x, x]](/sites/default/files/tex_cache/2063ace6deb2137a5301d18c08a7b22d.png) принадлежит
принадлежит  . По определению транзитивного замыкания существует последовательность
. По определению транзитивного замыкания существует последовательность  , такая, что все пары
, такая, что все пары ![[x_i, x_{i+1}]](/sites/default/files/tex_cache/b9ecd49b3245fff5c8a6ccb8e4a645be.png) для
для  принадлежат
принадлежат  и что
и что  и
и 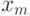 равны
равны  . Но это означает существование цикла для
. Но это означает существование цикла для  . Пришли к противоречию.
. Пришли к противоречию.
Этот результат позволяет нам рассматривать ациклическое отношение как "ядро" отношения порядка. Взятие транзитивного замыкания дает нам настоящее отношение порядка. Это соответствует интуитивному пониманию отношения, например, такого как before между стоящими перед нами задачами, – если задача Money должна предшествовать задаче Pass, а задача Pass должна предшествовать задаче Louvre, то мы понимаем, что задача Money должна предшествовать задаче Louvre. Другими словами, мы инстинктивно принимаем транзитивное замыкание. Но когда готовятся входные данные для задачи расписания или для другой задачи, в которой предполагается топологическая сортировка, то, естественно, хотелось бы перечислить только базисные ограничения, а не полное транзитивное замыкание. Вот почему топологическая сортировка может использовать ациклическое отношение на входе (многие представления топологической сортировки начинают с отношения порядка, но это избыточное требование, более строгое, чем требуется).
Вычисление транзитивного замыкания является "дорогой" вычислительной операцией, но нам не потребуется выполнять ее явно – алгоритм топологической сортировки будет работать с ациклическим отношением.