| Россия |
Проектирование и инженерия алгоритма: топологическая сортировка
10.4. Базисный алгоритм
Теперь мы можем приступить к полной реализации ключевой части нашего решения – процедуре process.
Цикл
Общий алгоритм этого метода уже написан, осталось адаптировать его с учетом всех сделанных уточнений (ослабление инварианта, использование метода sorted, представляющего результат в TOPOLOGICAL_SORTER). В результате получаем:
from
create {…} sorted. make
until
"Нет элемента без предшественников"
Loop
"Пусть x — элемент без предшественников"
sorted. extend (x)
"Удалить x из множества элементов"
Удалить все ограничения, начинающиеся с x
end
if "остался хоть один элемент" then — Отчет о цикле:
cycle_found:= True
"Вставьте эти элементы в cyclists"
end
Все, что осталось, – но не спешите слишком радоваться, главные трудности еще впереди, – это уточнить псевдокод, превратив его в код программный. Заключительная часть (отчет о циклах) будет прямым следствием всего остального. Главная задача состоит в уточнении четырех операторов псевдокода, точнее, трех, поскольку мы можем рассматривать первые два как одну операцию. Сосредоточимся на этих операциях в процессе поиска эффективного алгоритма.
Топологическая сортировка: базисные операции
Мы должны найти такие представления данных (множеств элементов и ограничений), которые делают эти операции эффективными, насколько это возможно. Структуры данных будут появляться как закрытые компоненты класса в разделах, резервированных для этих целей.
Приведенная выше схема класса оставила незаполненными тела двух методов класса: add_element и add_constraint. Нам предстоит дополнить методы, основываясь на структурах данных, которые мы сейчас спроектируем.
"Естественный" выбор структур данных
Для нашей первой попытки построения структуры данных естественно выбрать представление, которое непосредственно моделирует входные данные в том виде, как они к нам приходят (наш небольшой опыт в изучении программирования говорит, что не следует утверждать, что некоторое решение является "естественным". То, что кажется естественным мне, вовсе может не казаться таковым для вас, а то, что естественно для меня и для вас, может оказаться довольно посредственным решением).
Чаще всего входные данные могли бы поступать в виде списка элементов и списка ограничений. Мы могли бы использовать атрибуты класса, которые непосредственно отображают эти структуры данных (сделав их закрытыми для клиентов, размещая их в секции feature {NONE}):
elements: LINKED_LIST [G]
constraints: LINKED_LIST [TUPLE [G, G]]
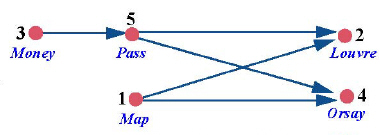
В нашем примере структуры данных будут выглядеть подобным образом:
Для простоты предполагается, что мы присвоили номера нашим элементам следующим образом ( рис. 10.12).
Анализ производительности естественного решения
Можем ли мы реализовать при таком представлении данных операции Т1, Т2, Т3 и процедуры record_element и record_constaint, и если да, то какова цена решения – сложность по времени и по памяти?
Две процедуры реализуются непосредственно. Например, для выполнения record_constaint достаточно вызывать стандартный метод:
constraints. extend ([x, y])
Новая пара [x,y] добавится в конец списка ограничений. Подобным образом record_element(x) реализуется вызовом elements.extend(x).
Это представление можно использовать и при реализации других операций. Давайте проанализируем их стоимость, когда у нас есть n элементов и m ограничений.
- Для поиска элемента без предшественников (T1) можно обойти список ограничений constaints и считать предшественников для каждого элемента, затем обойти список элементов для поиска тех, у кого число предшественников равно нулю. Первый обход потребует
 операций, второй –
операций, второй –  , и поскольку это нужно делать на каждом шаге, в целом понадобится операций
, и поскольку это нужно делать на каждом шаге, в целом понадобится операций  .
. - Удаление элемента (T2) требует на каждом шаге
 операций, а в целом –
операций, а в целом – 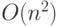 .
. - Удаление ограничений (T3) требует на каждом шаге
 операций, а в целом –
операций, а в целом –  . Предполагается, что мы имеем единый список ограничений, а потому для удаления элементов, начинающихся с некоторого заданного
. Предполагается, что мы имеем единый список ограничений, а потому для удаления элементов, начинающихся с некоторого заданного  , потребуется обход всего списка.
, потребуется обход всего списка.
В практических приложениях следует ожидать, что для каждого элемента задается несколько ограничений, так что  , а потому
, а потому  хуже, чем
хуже, чем 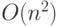 . Поскольку в реальных задачах
. Поскольку в реальных задачах  может быть велико, сложность
может быть велико, сложность 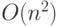 представляется неприемлемо высокой.
представляется неприемлемо высокой.
Так что наш первый выбор структуры данных дает решение задачи, но его производительность не позволяет построить масштабируемое приложение, пригодное для задач большой размерности.
Дублирование информации
К счастью, мы можем найти решение лучшее, чем "естественное". Как показывает опыт, мы не всегда должны использовать структуры данных в том виде, как они к нам приходят. Списки elements и constraints – это непосредственное отражение данных внешнего мира, естественного представления данных человеком, который вводит задачи и описывает ограничения между задачами. Но форма данных, простая и естественная для внешнего мира, вовсе не является лучшей формой для алгоритма, предназначенного для обработки этих данных некоторым специальным образом. Вместо того чтобы слепо следовать форме приходящих данных, алгоритм может начинаться с этапа инициализации, который преобразует данные в формат, наилучшим образом приспособленный к их обработке.
Следующие структуры данных помогают выполнить работу топологической сортировки – задачи Т1-Т3 – удобно и быстро:
successors: ARRAY [LINKED_LIST [INTEGER]]
— Индексами массива являются номера элементов. Для каждого элемента x
— задается список его непосредственных последователей – элементов y,
— таких, что есть ограничение [x, y].
predecessor_count: ARRAY [INTEGER]
— Индексами массива являются номера элементов.
— Для каждого элемента x указывается число его непосредственных
— предшественников.
Следующий рисунок иллюстрирует представление данных для нашего примера.
На следующем рисунке приведена уже хорошо нам знакомая схема, где введена нумерация элементов. Она поясняет предыдущий рисунок. По схеме ясно, что, например, у задачи 1 предшественников нет, но есть два последователя, а у задачи 5 – один предшественник и те же два последователя (2 и 4).
В этом представлении интересно то, что массив, задающий число предшественников, является избыточным, поскольку всю хранимую в нем информацию можно извлечь из массива последователей. Но ничего ошибочного в таком представлении информации нет, поскольку, как мы увидим, за счет этого дублирования можно добиться существенного улучшения времени вычислений.
Нахождение компромисса память-время является ключевой составляющей проектирования хорошего алгоритма. Конечно, компромисс должен быть приемлемым. В данном случае наша цель — получить алгоритм с временной сложностью O(m + n), сохраняя ту же сложность и для памяти, требуемой для хранения данных. Такая память нужна для хранения массива successors, добавление массива predecessor_count с емкостью O(n) не меняет емкостной сложности алгоритма в целом.
Исходные структуры данных – elements и constraints – также требуют памяти O(m + n).
Украсим алгоритм инвариантом класса
Удобно для пущей ясности добавить запрос, доступный клиентам:
count: INTEGER
— Число элементов
Также полезно для улучшения читабельности добавить инварианты класса. Два последних предложения выражены неформально:
elements.count = count
predecessor_count. count = count
successors.count = count
— Для каждого i из интервала 1..count элемент predecessor_count[i]
— задает число предшественников i-го элемента для заданных ограничений.
— Для каждого i из интервала 1..count элемент successors[i]
— задает список всех последователей i-го элемента для заданных ограничений
— или void, если последователей нет.