|
Непонятно почему в примере - отношение t НЕ транзитивно, ведь пары (2,4) и (4, 6) влекут (2, 6) и эта пара имеет общий делитель 2. |
Инспектор
Вы можете этот курс.
Опубликован: 21.03.2008 | Уровень: для всех | Доступ: платный | ВУЗ: Вятский государственный университет
Лекция 1:
Теория множеств
Операции над множествами
Рассмотрим такие операции над множествами, как объединение, пересечение, разность, симметрическая разность и дополнение.
Объединением множеств 
и 
( 
) называется множество, состоящее из всех тех элементов, которые принадлежат хотя бы одному из множеств или . (
рис.
1.3 ).
В общем случае операция объединения может быть использована для нескольких множеств: 
или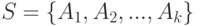 
.
Последнее можно представить в следующем виде:
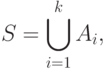
где 
- количество объединенных множеств.
Пример. Даны два множества: 
и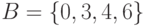 
. Найдем множество 
. 
.
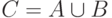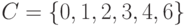Пересечением множеств и ( 
) называется множество, состоящее из элементов, входящих как в множество , так и в множество (
рис.
1.4 ):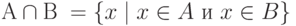 
.
Операция пересечения так же может быть многоместной: 
или
где - количество объединенных множеств 
.
Пример. Даны множества и 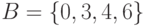. Найдем их пересечение: 
.
Разностью множеств и ( 
) называется множество всех элементов множества , которые не содержатся в ( рис. 1.5,а ):
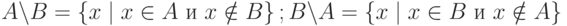( рис. 1.5,б ).
Пример. Даны два множества и . Найдем их разность.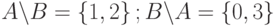 
.
Симметричная разность множеств и , ( 
): 
(
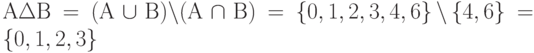рис.
1.6).
Дополнением (до универсального множества ) множества называется множество всех элементов, не принадлежащих , но принадлежащих универсальному множеству (
рис.
1.7).
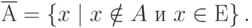
Пример. Пусть универсальное множество 
состоит из букв русского алфавита, - множество гласных букв, тогда 
- множество согласных букв и букв ь и ъ.
Приоритет выполнения операций: сначала выполняются операции дополнения, затем пересечения и только потом объединения и разности. Последовательность выполнения операций может быть изменена скобками.
Владислав Бариков
