Компьютерное моделирование и решение нелинейных уравнений

Метод Рунге - Кутта 4-го порядка

Самое большое распространение из всех численных методов решения дифференциальных уравнений с помощью ЭВМ получил метод Рунге-Кутта 4-го порядка. В литературе он известен как метод Рунге-Кутта.

В этом методе на каждом шаге интегрирования дифференциальных уравнений искомая функция y(x) аппроксимируется рядом Тейлора (12.4), содержащим члены ряда с h⁴:

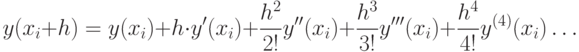
В результате ошибка на каждом шаге имеет порядок h⁵.

Для сохранения членов ряда, содержащих h²,h³,h⁴ необходимо определить вторую y", третью y"' и четвертую y⁽⁴⁾ производные функции y(x). Эти производные аппроксимируем разделенными разностями второго, третьего и четвертого порядков соответственно.

В результате для получения значения функции y_i+1 по методу Рунге-Кутта выполняется следующая последовательность вычислительных операций:

Вывод формулы не приведен. Предоставляется возможность вывод формул выполнить самостоятельно.

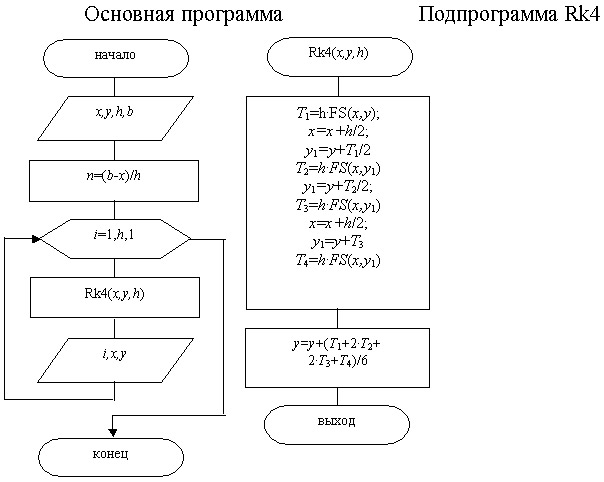
Алгоритм метода Рунге-Кутта (4-го порядка) можно построить в виде двух программных модулей: основной программы и подпрограммы Rk4, реализующей метод (рис 12.14).

Рис. 12.14. Схема алгоритма метода Рунге-Кутта 4-го порядка.

Здесь

(x,y) -при вводе начальная точка, далее текущие значения табличной функции,

h -шаг интегрирования дифференциального уравнения,

b -конец интервала интегрирования.