Генерирование на ЭВМ последовательностей равномерно распределенных случайных чисел. Моделирование нормально распределенной случайной величины

Теперь перейдем к генерированию последовательности нормально распределенных случайных чисел.

Рассмотрим датчик нормально распределенных случайных чисел.

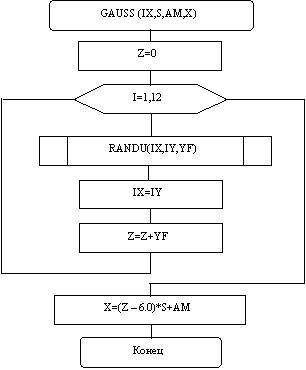
Алгоритм датчика (рис. 8.3) реализует метод получения последовательностей псевдослучайных чисел с нормальным законом распределения, основанный на центральной предельной теореме вероятностей. Алгоритм датчика требует обращения к RANDU для вычисления равномерно распределенных случайных чисел.

Назначение датчика GAUSS:

Вычисление нормально распределенного псевдослучайного числа X с заданным математическим ожиданием AM и среднеквадратичным отклонением S.

Обращение к датчику: GAUSS (IX,S,AM,X),

Описание параметров:

IX – параметр необходимый для обращения к RANDU. При первом обращении, IX – целое число с числом цифр 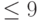. После первого обращения IX=IY, где IY – целое равномерно распределенное случайное число, вычисленное с помощью равномерно распределенных случайных чисел RANDU.

S – требуемое среднеквадратичное отклонение нормального распределения.

AM – требуемое математическое ожидание нормального распределения.

X – значение вычисленной нормально распределенной случайной величины.

Требуемые подпрограммы:

RANDU – датчик равномерно распределенных случайных чисел.

Обращение к RANDU:

RANDU (IX,IY,YF),

где

YF – полученное в результате обращения случайное равномерно распределенное число в интервале [0,1] и представленное в форме с плавающей запятой.

Рис. 8.3. Алгоритм датчика GAUSS

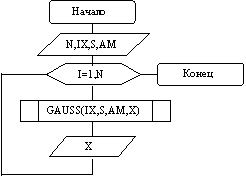
Используя датчик GAUSS, построим алгоритм (рис. 8.4) вычисления последовательности нормально распределенных случайных чисел X с требуемым математическим ожиданием AM и среднеквадратичным отклонением S.

Рис. 8.4. Алгоритм вычисления последовательности нормально распределенных случайных чисел

Исходные данные:

N - длина последовательности нормально распределенных чисел (количество испытаний).

IX - начальное значение, нечетное целое число с числом цифр .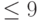

S, AM – характеристики нормального распределения: среднеквадратичное отклонение и математическое ожидание.

Результат:

X – значение нормального распределения псевдослучайного числа.

Используя различные начальные значения параметра IX, можно формировать различные последовательности нормального распределенных псевдослучайных чисел.