Генерирование на ЭВМ последовательностей равномерно распределенных случайных чисел. Моделирование нормально распределенной случайной величины

Алгоритм метода:

1. Выработать два независимых случайных числа y₁ и y₂, равномерно распределенных в интервале [0,1].
2. Установить:

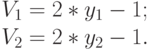
Теперь величины V₁ и V₂ равномерно распределены в интервале [-1;+1] и их удобно представить в форме с плавающей запятой.

1. Установить:
   
2. Проверить условие: 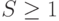Если "да ", то необходимо вернуться к шагу 1. Если "нет", то переходим к шагу 3.
3. Вычисляем x₁ и x₂:

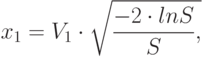
   ( 8.1)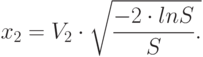

   

   Полученные величины x₁ и x₂ – это требующиеся значения нормально распределенных случайных величин со средним значением равным нулю, и среднеквадратичным отклонением .
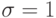4. При других значениях среднего и среднеквадратичного отклонения делаем пересчет:
   

Метод полярных координат легко доказать, воспользовавшись аналитической геометрией. Рассмотрим плоскость, определенную декартовыми координатами V₁ и V₂. С помощью шагов 1 и 2 метода мы получаем на плоскости равномерно распределенные случайные точки с декартовыми координатами (V₁,V₂) и полярными координатами 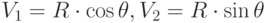, где R²=S. Далее, с помощью шагов 3 и 4 метода, мы из этих случайных точек оставляем только те точки, которые находятся внутри единичного круга.

При этом попадание точек внутрь единичного круга подчиняется закону нормального распределения со средним значением равным нулю, и среднеквадратичным отклонением равным единице.

Переходя к полярным координатам точек, которые равномерно распределены внутри единичного круга имеем

( 8.2)