Генерирование на ЭВМ последовательностей равномерно распределенных случайных чисел. Моделирование нормально распределенной случайной величины

Метод, основанный на центральной предельной теореме

Этот метод моделирования относится к третьему способу получения последовательности чисел с нормальным законом распределения. Метод основан на приближенном воспроизводстве условий, при которых справедлива центральная предельная теорема теории вероятности.

Согласно центральной предельной теореме, при сложении достаточно большого количества независимых случайных величин с произвольным законом распределения получается случайная величина, распределенная по нормальному закону. Опыт показывает, что при сложении всего шести (k=6) случайных величин равномерно распределенных на интервале [0,1], получается случайная величина, которая с точностью, достаточной для большинства прикладных задач, может считаться нормальной.

Рассмотрим метод аппроксимации нормально распределенной случайной величины Х, основанный на использовании двенадцати (k=12) равномерно распределенных случайных величин.

Алгоритм метода:

1. Сложить 12 равномерно распределенных псевдослучайных чисел y_i.
2. Пронормировать полученную сумму, т.е. получить случайную величину T с М(Т)=0 и 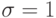, где Т – нормально распределенная случайная величина.
3. Результат привести в соответствие с заданным математическим ожиданием и среднеквадратичным отклонением .

Нормально распределенная случайная величина X с требуемыми значениями математического ожидания и среднеквадратичного отклонения определяется как:

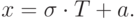
Пусть

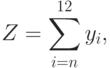
Ранее было показано, что математическое ожидание и дисперсия равномерно распределенной на интервале [0,1] случайной величины Y соответственно равны:

Тогда математическое ожидание суммы Z равно:

а ее дисперсия D(Z) равна:

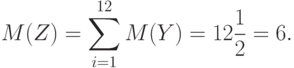
Пронормируем сумму Z, т.е. перейдем от нее к величине:

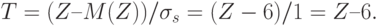
Переходя к требуемым математическому ожиданию a и среднеквадратичному отклонению , окончательно имеем:

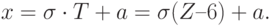
Таким образом, чтобы определить значение нормально распределенной случайной величины с математическим ожиданием, равным нулю, и среднеквадратичным отклонением, равным единице, необходимо взять 12 равномерно распределенных чисел, сложить их, а из суммы вычесть 6, т.е.:

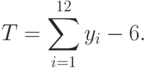( 8.4)

Чтобы определить значение нормально распределенной случайной величины с требуемым математическим ожиданием a и требуемым среднеквадратичным отклонением необходимо из суммы двенадцати равномерно распределенных чисел вычесть 6, а результат умножить на и прибавить a, т.е.

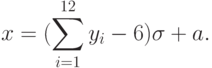( 8.5)