Лекция 11: Численное решение краевых задач для систем обыкновенных дифференциальных уравнений

10.6.2. Метод квазилинеаризации (метод Ньютона)

Рассмотрим простейшую разностную аппроксимацию краевой задачи для ОДУ второго порядка

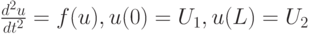
следующего вида:

Зададим некоторые начальные приближения 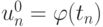к искомой функции и построим итерационный процесс, воспользовавшись линейным приближением функции правой части

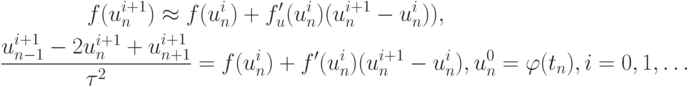
где i является итерационным индексом, а начальное приближение удовлетворяет граничным условиям

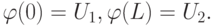
На первой итерации, т.е. при i = 0, получаем первое приближение к искомому решению, решая методом трехточечной прогонки разностное уравнение

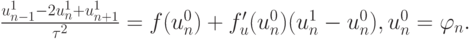
Полученное первое приближение вновь подставляем в линеаризованную разностную задачу и методом прогонки получаем второе приближение. Аналогично поступаем и далее, до достижения заданной точности в соответствии с условием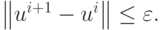

10.6.3. Аппроксимация граничных условий

Для простоты выше рассматривались краевые задачи, для которых задавались граничные условия первого рода, т.е. на границе рассматриваемой области задавалось значение функции. Тогда трудностей с аппроксимацией граничных условий не возникало. Несколько сложнее обстоит дело при задании граничных условий второго и третьего рода (условий на производные и смешанные условия). Ограничимся описанием способов аппроксимации лишь для граничных условий второго рода.

Рассмотрим вначале линейную задачу с постоянными коэффициентами

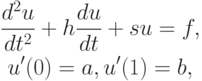
и соответствующую ей разностную задачу

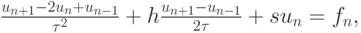
заменив при этом производные в граничных условиях по формулам односторонего дифференцирования первого порядка

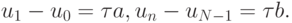
В результате получили разностную схему для аппроксимации дифференциальной задачи. Несмотря на то, что во внутренних узлах разностные формулы приближают дифференциальные уравнения со вторым порядком аппроксимации, решение по этой схеме получается только с первым порядком из - за понижения порядка аппроксимации в граничных точках. Естественно было бы повысить порядок схемы до второго во всех точках, включая граничные.

Наиболее распространены три способа.

1. Использование формул одностороннего дифференцирования более высокого порядка точности. Эти формулы разбирались в "Предмет вычислительной математики. Обусловленность задачи, устойчивость алгоритма, погрешности вычислений. Задача численного дифференцирования" . Подход очевиден, однако имеет недостаток — матрица системы уравнений для определения решения будет уже не трехдиагональной, следовательно, алгоритм прогонки неприменим. Можно избавиться от этого недостатка, проведя перед численным решением системы соответствующие алгебраические преобразования. Они в случае применения конкретной формулы численного дифференцирования для аппроксимации граничных условий свои, но достаточно очевидны.
2. Использование фиктивной ячейки (фиктивного узла). Рассмотрим расширение сеточной области. Введем в рассмотрение узлы с индексами 0 и N + 1, находящиеся формально за пределами рассматриваемой области. Пусть в них тоже определено значение сеточной функции. Тогда узел с индексом 0 выступает как внутренний узел, и в нем может быть записано соотношение
   

   при этом можно для граничного условия использовать формулу для вычисления производной со вторым порядком аппроксимации по формуле центральных разностей

   
   Из этих двух уравнений осталось только исключить значение в фиктивном узле (фиктивной ячейке).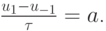

   Такой метод аппроксимации граничных условий очень хорошо зарекомендовал себя при решении нелинейных задач для уравнений в частных производных. В таком случае значения сеточной функции в фиктивных точках не исключаются из системы, а тоже находятся численно.

   На правом конце отрезка формулы аналогичны. Не составляет труда обобщить этот подход и для граничных условий третьего рода.
3. Использование ряда Тейлора. Для формулы на левой границы области интегрирования 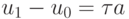в явном виде выпишем главный член невязки: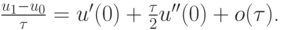
   

   Используя само дифференциальное уравнение, можно выразить значение второй производной функции в окрестности границы:

   

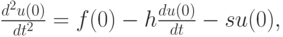
   откуда следует

   

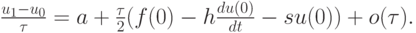
   Заменив в последнем соотношении производную на конечную разность, получим

   

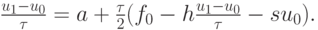
   Осталось только привести это соотношение к виду, удобному для использования в методе прогонки.

В случае линейных уравнений с постоянными коэффициентами два последних способа приводят к одному и тому же выражению для значения сеточной функции в граничном узле. Для нелинейных уравнений эти способы будут различаться, но каждый из них приводит к повышению порядка аппроксимации граничных условий и, следовательно, разностной схемы.