Лекция 11: Численное решение краевых задач для систем обыкновенных дифференциальных уравнений
Теперь, после того как описан прогоночный алгоритм, исследуем его на устойчивость.
Для этого рассмотрим вычисление прогоночного коэффициента pn (т.е. этап прямого хода прогонки). В идеальной арифметике этот коэффициент равен
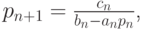
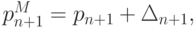 где
где 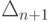 — погрешность, связанная с округлениями на всех предшествующих этапах вычислений. Полагая
— погрешность, связанная с округлениями на всех предшествующих этапах вычислений. Полагая 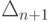 малой, исследуем изменение этой погрешности с ростом n. Для этого запишем соотношение между
малой, исследуем изменение этой погрешности с ростом n. Для этого запишем соотношение между 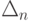 и
и 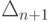 в виде
в виде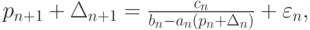
где  — погрешность вычислений правой части и машинного представления коэффициентов an, bn, cn. Следовательно,
— погрешность вычислений правой части и машинного представления коэффициентов an, bn, cn. Следовательно, 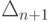 складывается из двух составляющих — локальной погрешности
складывается из двух составляющих — локальной погрешности  и наследственной
и наследственной 
Полагая 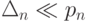 при
при 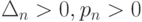 и опуская члены порядка
и опуская члены порядка 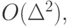 получим оценку
получим оценку
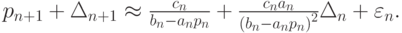
Отсюда, учитывая, что
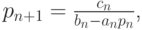
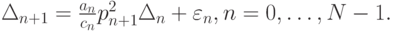 |
( 10.2) |
Докажем следующую теорему.
Теорема. Если выполнены условия диагонального преобладания 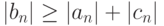 и хотя бы для одной строки матрицы системы имеет место строгое диагональное преобладание
и хотя бы для одной строки матрицы системы имеет место строгое диагональное преобладание 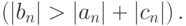 Пусть, кроме того, 0 < p1 < 1. Тогда алгоритм прогонки устойчив.
Пусть, кроме того, 0 < p1 < 1. Тогда алгоритм прогонки устойчив.
Доказательство.
Докажем утверждение теоремы для случая, когда во всех строках матрицы выполнено условие строгого диагонального преобладания. На случай нестрогих неравенств обобщение доказательства очевидно.
- Пусть выполнено условие диагонального преобладания и 0 < p1 < 1. Для определенности положим an > 0, bn > 0, cn > 0.
Тогда
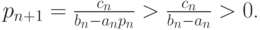
Кроме того,
откуда следует 0 < pn + 1 < 1.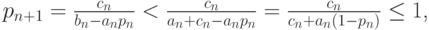
- Покажем, что
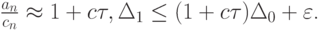
Для этого вспомним выражения для коэффициентов линейной системы, полученной при разностной аппроксимации исходного уравнения второго порядка.
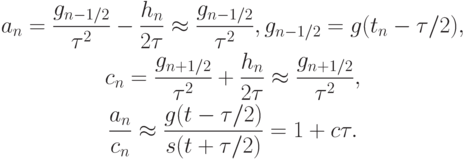
Вернемся к выражению для эволюции погрешности (10.2). С учетом полученных оценок имеем
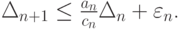
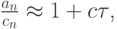
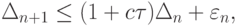 где c — константа Липшица для функции g(t). Считаем, что на каждом шаге ошибка округления не превосходит предельного значения, т.е.
где c — константа Липшица для функции g(t). Считаем, что на каждом шаге ошибка округления не превосходит предельного значения, т.е. 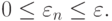
Из цепочки неравенств
![\begin{gather*}
\Delta_2 \le (1 + c\tau )^2 \Delta_0 + \varepsilon \left[{1 + (1 + c\tau )}\right], \\
\Delta_3 \le (1 + c\tau )^3 \Delta_0 + \varepsilon \left[{1 + (1 + c\tau ) + (1 + c\tau )^2 }\right],
\end{gather*}](/sites/default/files/tex_cache/11ddc82b50865d5b823a11105a0c5a47.png)
будет следовать оценка
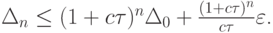
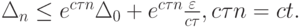
При 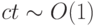 погрешности не накапливаются (для краевых задач это реальное условие), поскольку в расчетах
погрешности не накапливаются (для краевых задач это реальное условие), поскольку в расчетах  где
где  — машинный эпсилон (подробнее в
"Предмет вычислительной математики. Обусловленность задачи, устойчивость алгоритма, погрешности вычислений. Задача численного дифференцирования"
).
— машинный эпсилон (подробнее в
"Предмет вычислительной математики. Обусловленность задачи, устойчивость алгоритма, погрешности вычислений. Задача численного дифференцирования"
).
Аналогичное утверждение доказывается и для второго прогоночного коэффициента
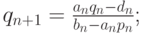
Покажем устойчивость обратного хода прогонки.
При обратном ходе вычисления проводятся по формулам un = pn + 1un + 1 + qn + 1, откуда, учитывая, что 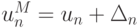 и
и 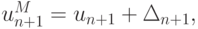 получим
получим 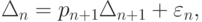 где
где 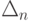 — наследственная погрешность,
— наследственная погрешность,  — погрешность округления на n шаге. Очевидно, что обратный ход прогонки устойчив при выполнении условия 0 < pn < 1, или 0 < p1 < 1.
— погрешность округления на n шаге. Очевидно, что обратный ход прогонки устойчив при выполнении условия 0 < pn < 1, или 0 < p1 < 1.
