Численные методы решения экстремальных задач
4.2. Методы спуска
Основная идея методов спуска состоит в том, чтобы построить алгоритм, позволяющий перейти из точки начального приближения  в следующую точку
в следующую точку  таким
образом, чтобы значение целевой функции приблизилось к минимальному.
таким
образом, чтобы значение целевой функции приблизилось к минимальному.
4.2.1. Метод покоординатного спуска
Этот метод является редукцией поиска функции многих переменных к последовательности поиска минимумов функции одной переменной. Пусть  — начальное приближение к минимуму
— начальное приближение к минимуму 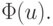
Рассмотрим  как функцию
одной переменной u1 при фиксированных
как функцию
одной переменной u1 при фиксированных  и находим одним из приведенных методов поиска минимума функции одной переменной
и находим одним из приведенных методов поиска минимума функции одной переменной

Полученное значение u1, доставляющее минимум  обозначим
обозначим 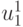 ; при этом
; при этом

Далее, при фиксированных значениях  ищем
ищем

как функции от u2 ; соответствующее значение u2 обозначим  ; при этом
; при этом

Этот процесс продолжаем аналогичным образом и для оставшихся координат; в результате получим

Таким образом, переходим из точки u0 в точку u1. Этот процесс повторяется до тех пор, пока не будет выполнено условие выхода из итераций, например:

где 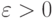 — заданная точность.
— заданная точность.
Пример. Найти минимум функции двух переменных

Выбрав некоторую точку начального приближения, например, u0 = (2,2), получим минимум целевой функции за два шага, так как ее линии уровня — окружности с центром в начале координат (рис. 4.2).
Если же целевой функцией является, например

которая поворотом системы координат на угол  и преобразованием
и преобразованием

приводится к виду  то ее линиями уровня являются эллипсы
то ее линиями уровня являются эллипсы  поэтому спуск будет иметь
иной характер (рис. 4.3).
поэтому спуск будет иметь
иной характер (рис. 4.3).


