SPMD-технология на базе симметричной ВС
Распараллеливание по двумерному опорному массиву
Построим программу умножения матриц C=A x B размерности k, где каждый элемент матрицы-результата C находится:
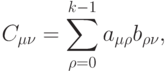
 — номер строки матрицы C ;
— номер строки матрицы C ;  — номер столбца.
— номер столбца.Представим множество элементов C одномерным массивом, обусловленным расположением подряд строк этой матрицы:
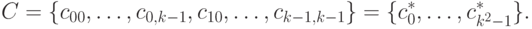
Пусть каждый процессор П i, i = 0,...,N-1, считает элементы c{i+jN}* этого массива, j = 0,1,....
Для построения подпрограммы нахождения скалярного произведения строки A и столбца 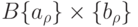 ,
, 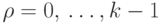 , сформируем дескрипторы с
дескрипторными элементами, необходимыми для организации счета только одним
процессором:
, сформируем дескрипторы с
дескрипторными элементами, необходимыми для организации счета только одним
процессором:
D1 = {D10, D11, D12, D13, D14} = {a0, 1, k, a0+k-1, a0},
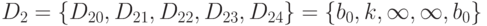 .
.
Указаны начальные значения D{14} и D{24}, а неиспользуемые значения D{22} и D{23} полагаются заведомо большими.
Так как мы условились распределять считаемые элементы массива C между процессорами, то сформируем на каждом процессоре дескриптор подмассива Ci закрепленных за ним элементов:
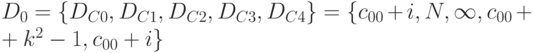
(указано начальное значение DC4, значение DC2 не используется).
Подпрограмма нахождения скалярного произведения приведена в табл. 12.3. Все используемые команды ранее встречались.
| №k | КОП | I1 | A1 | I2 | A2 | I3 | A3 |
|---|---|---|---|---|---|---|---|
| 0 | ЗАГ |  |
D14 | D10 | D24 | D20 | |
| 1 | ЦИКЛ | D12 | |||||
| 2 | x | D1 | D2 | ||||
| 3 | + |  |
 |
||||
| 4 | КЦ | ||||||
| 5 | ЗАП |  |
D3 | ||||
| 6 | В |
Использование в командах 2 и 5 адресов дескрипторов, которые, в отличие от адресов модификаторов и дескрипторных элементов, обладают специальным признаком, приводит к автоматической переадресации, производимой при выполнении этих же команд в цикле. Так, при выполнении команды 2, если (D14) не превосходит (D13), а (D24) не превосходит (D23), формируются исполнительные адреса A*1 = A1+(D14), A*2 = A2+(D24), после чего выполняются операции (D14) := (D14)+(D11) ; (D24) := (D24)+(D21). Это обусловило необходимость восстановления значений D14 и D24 по команде 0. Аналогично, при выполнении команды 5 готовится запись при следующем обращении к подпрограмме, (D34) := (D34)+N.
Пусть матрице A соответствует дескриптор массива первых элементов ее строк, то есть дескриптор первого столбца
DA = {DA0, DA1, DA2, DA3, DA4} = {a00, k, k, a00+(k-1)k, a00}
(указано начальное значение D{A4} ). Матрица B представлена дескриптором массива первых элементов ее столбцов, то есть дескриптором первой строки
DB = {DB0,...,DB7} = {b00, 1, k, b00+k-1, b00, b00+i, N, b00+i}
(указаны начальные значения DB4 и DB7 ). Программа умножения матриц (пропущены команды формирования и восстановления дескрипторов) представлена в табл. 12.4.
| №k | КОП | I1 | A1 | I2 | A2 | I3 | A3 |
|---|---|---|---|---|---|---|---|
| 10 | ПРАД | DB7 | 017 | ||||
| 11 | ПРАД | DA7 | 020 | ||||
| 12 | ЗАГ | D10 | DA4 | D13 | DA4 | D20 | DB7 |
| 13 | М+ | D13 | <k-1> | ||||
| 14 | БПВ1 | 000 | |||||
| 15 | ИЗМАД | DB7 | 017 | ||||
| 16 | БП | 012 | |||||
| 17 | М- | DB7 | DB2 | ||||
| 18 | М+ | DA4 | DA1 | ||||
| 19 | БП | 010 | |||||
| 20 | В |
По команде 10, выполняющейся первый раз при (DB7) = b00+i, адрес, записанный в DB7, сравнивается с адресом последнего элемента массива, записанным в DB3. Если адрес указывает на принадлежность элемента массиву, выполняется следующая команда. В противном случае управление передается на выполнение команды 17.
По команде 11 производится аналогичная проверка принадлежности элемента используемой строки матрицы A, адрес которого указан в DA4, массиву первых элементов ее строк. Если (DA4) > (DA3), управление передается на выполнение команды 20 — выход из подпрограммы.
По командам 12—13 формируются дескрипторные элементы дескрипторов D1 и D2 для скалярного умножения очередной строки матрицы A на очередной столбец матрицы B — для получения очередного элемента матрицы C.
По команде 14 производится обращение с возвратом в рамках одной задачи (без использования ОС) к процедуре счета скалярного произведения (см. табл. 12.3).
По команде 15 производится изменение адреса начального элемента столбца — переход к следующему столбцу с учетом предполагаемого закрепления элементов матрицы C за процессорами, а именно, производится операция (DB7) := (DB7)+(DB6), где (DB6) = N. Если после изменения адреса новое его значение превышает максимальное, записанное в DB3, осуществляется переход на выполнение команды 17. В~противном случае по команде 16 управление передается на выполнение команды 12 — на подготовку счета и счет очередного элемента C.
Команды 17 и 18 выполняются в случае, если измененный на значение N адрес (DB7) первого элемента столбца B превышает значение (DB3) = b00+k-1. Чтобы получить "координаты" того элемента C, к счету которого необходимо перейти, т.е. чтобы получить адреса первого элемента столбца и первого элемента строки, на пересечении которых он находится, необходимо выполнить следующие действия: последовательно вычитать шаг (DB2), т.е. значение k, из вновь полученного адреса столбца B и прибавлять шаг ( DA1 ), т.е. это же значение k, к ранее использованному адресу первого элемента строки A (первоначально — к значению a00 ) до тех пор, пока значение ( DB7 ) не станет меньше или равно значению ( DB3 ). По данным командам изменяются значения ( DB7 ) и ( DA4 ). Затем по команде 19 управление передается на выполнение команды 10, по которой в случае недостаточности коррекции дескрипторного элемента DB7 управление вновь передается на выполнение команды 17. Если коррекция элемента DB7 произведена успешно, по команде 11 может быть выяснено, что скорректированное значение ( DA4 ) превосходит значение ( DA3 ). Это означает, что следующий элемент матрицы C, к счету которого пытается приступить процессор, принадлежит несуществующей строке, то есть процессор закончил выполнение своей доли работы. По команде 20 производится выход из подпрограммы.

