Вычислительные системы нетрадиционной архитектуры

Однородные вычислительные структуры (среды)

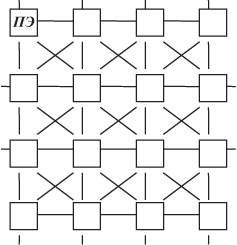
Однородные вычислительные структуры или среды (ОВС), как правило, относятся к типу МКМД и представляют собой регулярную решетку из однотипных процессорных элементов (ПЭ).

Каждый ПЭ обладает алгоритмически полным набором операций, а также операциями обмена или взаимодействия с другими ПЭ. Например, решетка с регулярными связями процессоров может быть такой, какая изображена на рис. 9.1.

Рис. 9.1. Однородная вычислительная среда

ОВС относится к ВС с распределенной памятью. Реализуется на основе микропроцессоров.

С 1985 г. стало развиваться направление разработки транспьютеров — в интегральном исполнении соответствующих ПЭ ОВС. Т.е. ОВС в этом случае строится как транспьютерная сеть.

Транспьютер — интегрально (в одном чипе или кристалле) выполненное семейство системных компонент, в составе которых: процессор, таймер, память, каналы последовательного ввода-вывода, контроллер внешней оперативной памяти.

Транспьютер вместе с языком программирования Occam (основной язык программирования транспьютеров) позволяет создавать ВС типа МКМД.

Легко видеть, что актуальность транспьютеров значительно снижается в связи с развитием интеграции при построении микропроцессоров, с развитием их функций. Мы видели, что современный микропроцессор значительно превысил те функции, в том числе по обеспечению взаимодействия, которые предполагалось реализовать в транспьютере.

На ОВС можно строить вычислительные процессы по разным схемам. Хорошо реализуются конечно-разностные схемы, обработки изображений, геофизические задачи, моделирования поведения среды (аэродинамические и гидродинамические задачи).

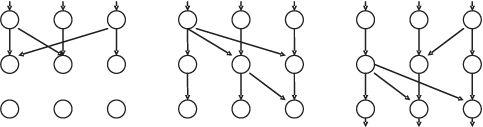
Систолическая схема вычислений. Представляет собой конвейер, в котором данные проходят обработку "волной" с одной границы ОВС — входа к другой границе — выходу. Следом за одной может следовать другая волна и т.д. (рис. 9.2). В этом случае ОВС — систолическая матрица.

Рис. 9.2. Схема систолических вычислений

На рисунке: в первом такте на вход подаются данные задачи 2, а задача 1 решается процессорами первой строки систолической матрицы; в следующем такте задача 2 решается первым уровнем, а задача 1 — вторым уровнем процессоров, на вход подаются данные задачи 3; на третьем уровне происходит очередное аналогичное смещение и т.д. Стрелками показано возможное перемещение обрабатываемой информации.

Ранее отмечалось, что фактически конвейеры в составе многофункциональных АЛУ строятся для каждой операции отдельно. Есть конвейеры сложения, умножения и т.д.

Однако систолическая схема вычислений позволяет построить универсальный программируемый конвейер, настраивая каждую строку матрицы процессоров на параллельное выполнение уровней конвейеров различных операций в порядке их следования. То есть операции могут динамически загружать систолическую схему, как это обусловлено следованием команд выполняемой программы.

Таким образом, в систолической матрице процессоров, ориентированной на применение в АЛУ, распараллеливание "в длину" успешно сочетается с распараллеливанием "в ширину", как и при решении произвольного потока задач.

С помощью ОВС реализуется и ВС типа "гиперкуб".

Гиперкуб — пространственное обобщение рассмотренной плоской решетки, где адресация процессоров (и соответственно, блоков распределенной памяти) ставится в зависимость от структуры связей между ними. Проводится аналогия с n -мерным пространством.

Рис. 9.3. Вычислительная система "гиперкуб": а — двумерный, б — трёхмерный, в — четырёхмерный

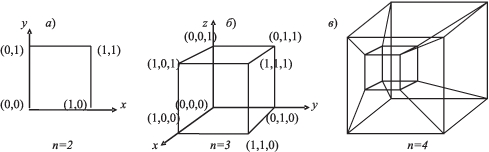
Возьмем единичный квадрат в двухмерном пространстве с вершиной в начале координат (рис. 9.3,а). Пусть его вершины соответствуют процессорным элементам (ПЭ), а ребра — связям между ними. Пусть код, образованный координатами вершин, — адрес ПЭ. Тогда видно, что связи между ПЭ существуют тогда, когда адреса отличаются не более чем в одном разряде.

То же самое можно обнаружить для n = 3 (рис. 9.3,б), n = 4 (рис. 9.3,в) и т.д.

Значит, в общем случае ВС типа "гиперкуб" формируется следующим образом. Ее образуют 2ⁿ ПЭ, каждый ПЭ соединен ровно с n ПЭ. При длине адреса ПЭ, равной n, непосредственно связаны ПЭ, у которых адреса разнятся не более чем в одном разряде.

Структура типа "гиперкуб" обладает важными свойствами.

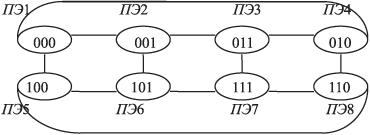
1. Из структуры "гиперкуб" легко получаются более простые структуры. Например, при n = 3 легко получается матричная ВС, на которой, в частности, хорошо решать задачи в конечных разностях. Как мы видели ранее, для этого удобна плоская решетка, где существуют непосредственные (не транзитные) связи между тремя ПЭ (столбец составляют только два ПЭ, поэтому нет необходимости в связях в двух направлениях), как показано на рис. 9.4. Здесь можно в дополнение к адресам ввести (временно) нумерацию ПЭ и поставить эти номера в соответствие адресам.

   

   
   Рис. 9.4. Матричная ВС на основе двумерного гиперкуба

   Процессоры образовали фрагмент плоской решетки для реализации конечно-разностного метода (метода сеток). Процессоры "прокатываются" по области, на которой строится решение, например, задачи численного интегрирования.

2. Второе важное свойство "гиперкуба" — возможность выделения задаче необходимых связных областей вычислительных ресурсов. Эти области соответствуют пространствам меньшей размерности, чем размерность всего "гиперкуба". Это означает, что т.к. процессоры адресуемы внутри некоторого адресного пространства, то каждой решаемой задаче может быть выделен вычислительный ресурс в пределах какого-то массива со сквозной нумерацией процессоров. В n -мерном пространстве этот массив принадлежит подпространству меньшего измерения. Т.е. значительная часть разрядов адреса длины n для всех процессоров, образующих ресурс данной задачи, совпадает, а меняются только несколько последних разрядов.

Например, предположим, что в предыдущем примере мы располагали не 3-мерным, а 6-мерным "гиперкубом". Пусть планирующая система в составе ОС из всего адресного пространства ПЭ выделила нам массив , т.е. определенное 3-хмерное подпространство всего пространства процессоров. В это же время пусть другой задаче выделен массив , т.е. четырехмерное подпространство и т.д.

Как и для других ОВС, здесь предполагается наличие распределенной памяти. При формировании общего адресного пространства примем, что старшие разряды адреса памяти совпадают с адресом ПЭ.