Параллельная обработка стека и статическое распараллеливание в решающем поле

Подстеки и их взаимодействие

В процессорах супер-ЭВМ используются многофункциональные АЛУ, состоящие из специализированных по операциям исполнительных устройств. Широкое применение микропроцессоров позволяет реализовать в составе АЛУ решающие поля на основе универсальных исполнительных устройств, которые могут выполнять последовательности команд или целые процедуры. Рассмотрим возможность динамического распараллеливания в таких АЛУ при выполнении арифметических операторов программы в безадресной системе команд процессора, воспроизводящей выполнение работ на стеке.

Существуют пути обобщения такой структуры ВС на основе комплектации многопроцессорных ВС на общем вычислительном ресурсе, - решающем поле. Такая структура в наибольшей степени адекватна концепции двух основных уровней распараллеливания: уровня программ и уровня команд.

Процессор в обычном смысле выполняет функции устройства управления - управления выполнением программы. Исполнительные команды выполняются процессорными элементами (ПЭ) решающего поля РП, которые составляют общий вычислительный ресурс ВС. Т.е. РП выполняет заявки процессоров на выполнение операций. При этом порядок использования ПЭ определяется динамически в соответствии с потоком команд программы и с возможностями их параллельного выполнения.

Однако при такой структуре и универсальности ПЭ целесообразно распределять между ними не отдельные команды, а группы команд или законченные операторы. И принимать решение об этом можно на основе анализа бесскобочной записи (польской инверсной записи — ПОЛИЗ) арифметических операторов программы, или, что то же самое, — на основе потока безадресных команд программы. Выясняется, что производить распределение (распараллеливание) можно, минуя промежуточный перевод команд из безадресной формы в трехадресную, — непосредственно по тексту программы.

Тогда, если представить, что программа в ПОЛИЗ предполагает ее непосредственное выполнение на стеке, то, следовательно, производится распараллеливание обработки стека. Работа одного стека сводится к параллельной работе нескольких взаимосвязанных подстеков данного стека. Каждый подстек реализуется на стеке выделенного для этого ПЭ. Если предположить, что данные находятся в СОЗУ и не подлежат перемещению при организации совместной работы ПЭ, то для их обработки целесообразно организовать в локальной регистровой памяти каждого ПЭ адресные стеки, как это рассматривалось выше.

Процессорный элемент и его адресный стек со своим окружением показан на рисунке 4.1.

Рис. 4.1. Подстек

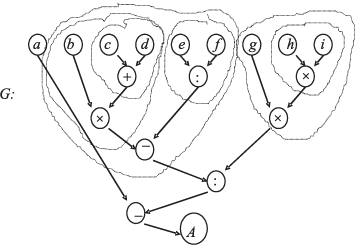
Рассмотрим арифметическое выражение

A := a - (b x (c + d) - e : f) : (g x h x i)

Его бесскобочная запись

Aabcd + x ef : - gh x i x : - :=.

Запишем программу, произведя очевидное оптимизирующее преобразование, сокращающее количество цепочек имен и операций,

abcd + x ef : - ghi x x : - ЗпА.

Составим информационный граф G, соответствующий порядку выполнения операций на стеке при счете значения этого выражения (рис. 4.2).

Рис. 4.2. Граф-схема счёта арифметического выражения

Строить этот граф будем в порядке выполнения операций. Сначала изобразим вершины a,b,c,d в соответствии с вызовом их в стек. Затем изобразим вершину +, соответствующую сложению c и d. Затем — вершину x, соответствующую умножению b на c+d. Так как цепочка операций закончилась, изобразим вершины e и f и т.д. В результате последовательных действий развернется граф G, иллюстрирующий параллельную структуру алгоритма счета значения данного выражения. Выделены подструктуры, которые могут выполняться параллельно.

Важный вывод на основе анализа графа: можно независимо (и параллельно) извлекать из памяти величины по всем именам, составляющим цепочки имен в ПОЛИЗ. Т.е. можно их заблаговременно считывать в любой последовательности, в том числе и параллельно. Однако при возможности последовательного обращения к памяти предпочтительным является анализ цепочек имен слева направо, а каждой цепочки — справа налево, т.к. использование величин в операциях производится справа налево. (В нижеследующих примерах загрузка стеков производилась традиционно.)

Тогда разовьем стековый механизм, позволяющий производить распараллеливание вычислений.

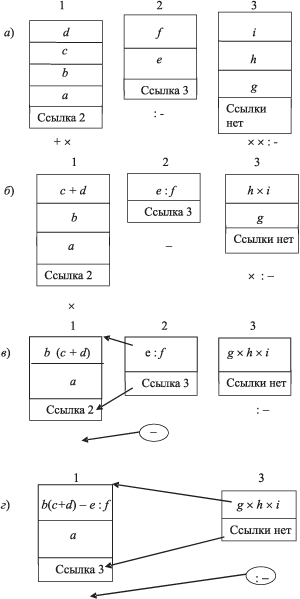
По числу цепочек имен (и операций) в ПОЛИЗ сформируем несколько подстеков, каждый из которых имеет свою вершину. Подстеки, сформированные для счета одного выражения, упорядочены так, что каждый из них может обладать ссылкой на свой правый подстек (кроме последнего). Левый по отношению к данному подстек образуется цепочкой имен, находящейся в бесскобочной записи непосредственно левее цепочки имен, соответствующей данному подстеку. Каждому подстеку ставится в соответствие следующая за цепочкой имен цепочка операций и разрешается ее выполнение. На рисунке 4.3,а показаны сформированные подстеки и их начальная загрузка (не по стековому принципу — последовательно через вершину, а по возможности параллельно или с перекрытием во времени).

Рис. 4.3. Взаимодействие подстеков

Определим возможный вариант реализации: подстеки могут заполняться не соответствующими величинами, а их адресами в СОЗУ. Т.е. традиционные приемы использования КЭШ-памяти должны быть применены здесь.

Взаимосвязь подстеков следует из неравенства длин цепочек имен и соответствующих им цепочек операций. Возможны ситуации:

1. подстек выродился в свою вершину, но цепочка операций оказалась не исчерпанной при том, что первая из этих операций - двуместная; такой подстек назовем не полностью вырожденным;
2. цепочка операций исчерпалась, но на подстеке содержится одна или более величин (или их имен, адресов), — такой подстек назовем вырожденным; если на подстеке находится единственная величина, составляющая вершину, то такой стек назовем полностью вырожденным.

Если данный подстек не полностью вырожденный, то последующая операция возможна над вершиной этого подстека и вершиной левого подстека, если тот является вырожденным или полностью вырожденным.

Если левый подстек также не полностью вырожденный или выполнение на нем возможных операций не закончилось, то данный подстек находится в состоянии ожидания. Для выполнения операции над вершинами двух подстеков (если правый подстек является вырожденным) правый подстек переводится на данный подстек так, что его вершина становится новой вершиной данного левого подстека. Ссылка правого подстека заменяет собой ссылку левого подстека. Таким образом, на основе двух подстеков формируется один и появляется возможность дальнейшего выполнения операций из цепочки.

При правильной бесскобочной записи каждый не полностью вырожденный подстек дождется возможности продолжения выполнения операций за счет вырожденного или полностью вырожденного левого подстека. Он, в свою очередь, превратится в вырожденный или полностью вырожденный и пополнит левый не полностью вырожденный, если такой имеется. Окончательное значение данного выражения образуется в вершине единственного оставшегося полностью вырожденного подстека, не содержащего ссылку на правый подстек.

Продолжим рассмотрение примера, для простоты считая одинаковым время выполнения всех операций.

На первом шаге (в первом такте) выполняются операции на всех подстеках (рис. 4.3,б). После этого подстек 2 оказывается не полностью вырожденным; в дальнейшем он будет ждать вырождения левого — подстека 1.

После выполнения операций на втором шаге (рис. 4.3,в) подстек 1 оказывается вырожденным, его дополняет подстек 2 со своей ссылкой на третий подстек, который становится правым для первого. Подстек 3 оказывается не полностью вырожденным, он ждет вырождения своего левого подстека.

После выполнения операций на третьем шаге (рис. 4.3,г) подстек 1 оказывается вырожденным; он дополняется подстеком 3.

После выполнения операций на подстеке 1 на четвертом и пятом шагах получается окончательный результат.

При произвольных временах выполнения операций динамическая картина меняется, но правила взаимодействия подстеков те же.

Таким образом, все подстеки образуют очередь заданий, которые распределяются между операционными или исполнительными универсальными устройствами — ПЭ для выполнения. ПЭ действительно образуют распределяемый ресурс системы, в общем случае — многопроцессорной, и назначаются динамически по необходимости. Реализуется концепция виртуальных исполнительных устройств или процессорных элементов решающего поля.

Усложним пример, введя в рассмотрение арифметические операторы, содержащие условие, а также образующие сложные конструкции с использованием условий.

Пусть необходимо распараллелить счет арифметического выражения

Y:=(a+e:f)x if axl <= c then if l < gxh then A else A+l else cx(h+16).

Предварительно необходимо распространить правила формирования ПОЛИЗ для отображения условий. Целесообразно оставлять на месте разграничители if, then, else. Знак операции, в которой участвует условное выражение, необходимо предпосылать каждому альтернативному оператору.

Тогда легко на этом примере представить формирование безадресной программы счета значения арифметического выражения:

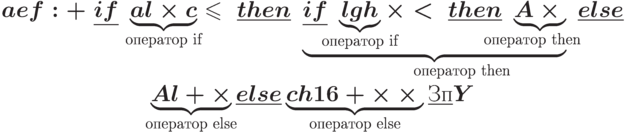
Процессор, как указывалось ранее, выполняя функции лишь устройства управления, производит последовательный анализ символов программы. Обнаружив цепочку имен, он выделяет ПЭ и настраивает его на обработку этой цепочки и последующей цепочки операций. При нахождении каждой следующей цепочки имен, если анализ производится вне условного оператора, он формирует ссылку "левого" подстека на свой "правый". Однако после формирования последнего (а возможно — единственного) подстека оператора if он формирует ему ссылку на два подстека: первого подстека оператора then и первого подстека оператора else — после их анализа.