Оптимальное программирование процессоров EPIC-архитектуры
Оптимизация ветвления при решении задач сортировки на процессоре EPIC-архитектуры
Выше предложен алгоритм компоновки "длинных" командных слов внутри линейного участка программы для VLIW -архитектуры, которые затем могут быть преобразованы в командные слова EPIC -архитектуры — в частности, сжатые и имеющие переменную длину. Логические конструкции разрешались на основе команды if-then-else, предполагающей немедленное (без возможности предварительного запоминания) использование предиката — значения булевой переменной. Это обусловило планирование одновременного выполнения оператора-условия и альтернативных операторов счета от момента ветвления "назад". Однако наличие регистровой памяти для хранения предикатов, задающих ветвление, значительно расширяет возможности EPIC -архитектуры. Альтернативный счет или ветвление по времени могут быть отделены от счета значения условия, предварительно найденного и хранимого. Поэтому такую важность получает применение методов диспетчирования параллельного вычислительного процесса не только при трансляции программ, но и при эвристическом оптимальном программировании "вручную".
Очевидно, что для разных задач различна и актуальность механизмов ветвления. Существуют задачи, для которых этот механизм является основным средством решения. По-видимому, такие задачи целесообразно выбрать в качестве тестовых для оценки эффективности ветвления.
В теории алгоритмов на задачах сортировки принято оценивать возможность снижения сложности алгоритмов. Основным элементом решения этих задач являются альтернативные действия, исключающие счет и основанные только на пересылках данных. Таким образом, основная нагрузка приходится на механизмы ветвления.
Понятие сложности определяется характером зависимости времени выполнения
алгоритма от основных параметров — размера задачи, длины массива и т.д. При этом важна
не точная зависимость, а именно ее характер, в связи с чем на самом высоком уровне
сложность делится на полиномиальную и экспоненциальную. Полиномиальная
сложность может характеризоваться максимальной степенью вхождения основного параметра в
эту зависимость. Так, например, сложность 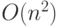 "пузырькового" алгоритма сортировки в
результате ухищрений может быть снижена до оценки O(n log2n),
где n — длина массива.
"пузырькового" алгоритма сортировки в
результате ухищрений может быть снижена до оценки O(n log2n),
где n — длина массива.
Однако выше речь идет о сложности алгоритма, а не о его реализации на компьютере. Компьютер, в результате слабой "профпригодности", может внести значительные коррективы сложности в худшую сторону.
Конечно, не всегда в этом случае виноват компьютер. При расчете сложности зачастую не учитываются объективно существующие затраты на организацию вычислительного процесса. Например, древовидная (графовая) структура требует значительных вычислительных затрат на обслуживание. Человек, производя сортировку "вручную", на неформальном уровне с легкостью производит логические действия, которые весьма трудоемки для компьютера.
Таким образом, необходимо:
- представить обобщенную программистскую модель процессора EPIC -архитектуры;
- произвести экспериментальное, "вручную", достаточно детальное планирование программ сортировки различными методами, преследуя цель минимизации времени (числа тактов) решения.
В то же время, составляя планы программ сортировки, будем высказывать предположения или рекомендации относительно возможностей системы команд процессора.
Обобщенная программистская модель процессора EPIC-архитектуры
Под программистской моделью понимают то, что "видит" программист (транслятор) в вычислительной системе и что достаточно для написания "хорошей" программы. Ранее это называлось "инструкцией пользователю", однако применительно к современной архитектуре требуются более глубокие знания принципов работы оборудования.
Так как нас интересует программа в виде расписания работы исполнительных устройств (ИУ) арифметическо-логического устройства (АЛУ), будем составлять планы компоновки таких расписаний, ориентируясь на VLIW -архитектуру, т.е. на EPIC -архитектуру в "распакованном" виде, где позиции слов (слоги) закреплены за ИУ. Ограничиваясь планированием "длинных" команд, будем составлять блок-схему с выделением строк блоков — прообразов команд и с расположением блоков в столбцах, соответствующих ИУ.
Для данной задачи достаточно рассматривать два логических ИУ. Пусть также используются два ИУ обмена информацией. Для оценки принципиальных возможностей оптимального программирования указанные параметры АЛУ несущественны.
Предположим, что все ИУ конвейерные, т.е. известно количество тактов счета результатов. Существуют средства синхронизации, при которых по указанному адресу записи считывание невозможно до окончания этой записи. При "близком" расположении команды, использующей нерассчитанный результат, автоматически выполняется пропуск такта (тактов), т.е. команда NOP (No Operation). (Технически такая синхронизация производится либо на основе взаимного анализа адресов текущего контекста, либо с помощью битов значимости регистров, "взводимых" при организации записи в эти регистры и "сбрасываемых" при окончании записи, что разрешает считывание из этих регистров.)
Предикатные (логические) вычисления выполняются с помощью адресуемой памяти (файла) предикатов 11Вопреки традиции, более правильно — значений предикатов.. Значения предикатов — булевых переменных рассчитываются логическими ИУ. В каждом слоге команды может быть указан адрес (имя) предиката для спeкулятивных вычислений, т.е. для выполнения (невыполнения) инструкции в зависимости от значения соответствующей булевой переменной.
Предполагается аппаратная поддержка циклов, основанная на автоматическом переиспользовании (переименовании) регистров и исключающая остановки конвейера выполнения команд.
Сортировка с помощью прямого включения
Целью сортировки является переформирование массива данных в порядке их невозрастания.
Данный метод заключается в том, что исходный массив условно делится на две части: уже отсортированную и еще не отсортированную. Первоначально отсортированная часть содержит лишь один, первый, элемент массива. Затем на каждом шаге первый элемент неотсортированной части вставляется в отсортированную часть на свое место с учетом упорядоченности.
Пусть задан массив a[1...12] = {6, 2, 4, 3, 4, 7, 10, 9, 5, 8, 0, 1}. В табл. 8.1 отражен процесс сортировки по шагам, где курсивом выделена упорядоченная часть массива.
Известны [10] оценки общего числа Cср сравнений и Mпер пересылок:
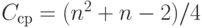 ,
,
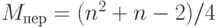 ,
,
что подтверждает оценку 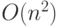 .
.
| Исходный массив | 6 | 2 | 4 | 3 | 4 | 7 | 10 | 9 | 5 | 8 | 0 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Шаг 1 | 2 | 6 | 4 | 3 | 4 | 7 | 10 | 9 | 5 | 8 | 0 | 1 |
| Шаг 2 | 2 | 4 | 6 | 3 | 4 | 7 | 10 | 9 | 5 | 8 | 0 | 1 |
| Шаг 3 | 2 | 3 | 4 | 6 | 4 | 7 | 10 | 9 | 5 | 8 | 0 | 1 |
| Шаг 4 | 2 | 3 | 4 | 4 | 6 | 7 | 10 | 9 | 5 | 8 | 0 | 1 |
| Шаг 5 | 2 | 3 | 4 | 4 | 6 | 7 | 10 | 9 | 5 | 8 | 0 | 1 |
| Шаг 6 | 2 | 3 | 4 | 4 | 6 | 7 | 10 | 9 | 5 | 8 | 0 | 1 |
| Шаг 7 | 2 | 3 | 4 | 4 | 6 | 7 | 9 | 10 | 5 | 8 | 0 | 1 |
| Шаг 8 | 2 | 3 | 4 | 4 | 5 | 6 | 7 | 9 | 10 | 8 | 0 | 1 |
| Шаг 9 | 2 | 3 | 4 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 0 | 1 |
| Шаг 10 | 0 | 2 | 3 | 4 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 1 |
| Шаг 11 | 0 | 1 | 2 | 3 | 4 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Однако, пытаясь запрограммировать этот метод для параллельного АЛУ, мы сталкиваемся с преобладанием операций, выполняемых над элементами массива строго последовательно:
- размещение каждого элемента в уже упорядоченной части массива должно быть выполнено до конца, т.к. размещение каждого предыдущего элемента позволяет начать размещение следующего;
- поиск места расположения очередного элемента сопровождается последовательным анализом и перемещением пропускаемых элементов.
Метод явно нуждается в модификации, что при наличии других, ниже рассматриваемых, методов сортировки вряд ли целесообразно.
