НОУ ИНТУИТ | Сервисы MATHCAD 14: реализация технологий экономико-математического моделирования. Лекция 1: Математические методы в моделировании экономики

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Опубликован: 27.05.2014 | Уровень: для всех | Доступ: платный | ВУЗ: Уральский государственный экономический университет

|

Вам нравится? Нравится 25 студентам

| Поделиться |

Поддержать программу

Исследование функций

Построение функциональной зависимости - один из основных математических инструментов моделирования взаимосвязей между различными экономическими характеристиками и показателями, описания и представления исследуемого процесса. Математическое исследование поведения функции, описывающей исследуемый экономический показатель: определение области допустимых значений, точек экстремума, асимптот, точек перегиба, дает необходимую информацию для экономического анализа. Представление графика функции позволяет визуально представить взаимосвязь, проследить ход процесса.

Пример 1.8.

Зависимость исследуемого экономического показателя от устанавливаемого фактора описывается функцией $y(x)=\sqrt[3]{x^2\cdot(x+4)}$ . Исследовать свойства показателя при изменении фактора: нулевые значения, экстремальные точки, асимптоты, особые точки.

На рисунке 1.6 показан листинг Mathcad, на котором показано, как рассчитать основные характеристики функции, провести их анализ, сделать выводы о характере зависимости.

Рис. 1.6. Пример исследования функции

$y(x):=\sqrt[3]{x^2\cdot(x+4)}$

Нули функции: 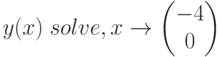$y(x)\; solve,x\to \begin{pmatrix} -4 \\ 0 \end{pmatrix}$

Пересечение с осью Ox: 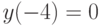y(-4)=0 , y(0)=0

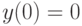
Возможные точки экстремума. Вычислим производную:

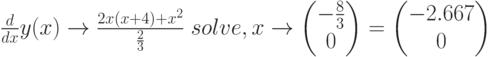
$\frac{d}{dx}y(x)\to \frac{2x(x+4)+x^2}{\frac{2}{3}}\; solve,x\to \begin{pmatrix} -\frac{8}{3} \\ 0 \end{pmatrix}=\begin{pmatrix} -2.667 \\ 0 \end{pmatrix}$

$3\cdot[x^2\cdot(x+4)]^3$

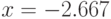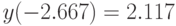
В точке x=-2.667 функция имеет экстремум (максимум, для x<0 ): y(-2.667)=2.117

В точке 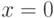x=0 локальный экстремум (минимум):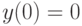 y(0)=0

Наклонная асимптота 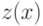z(x) определяется уравнением:

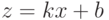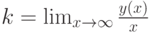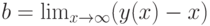
z=kx+b , где $k=\lim_{x \to \infty}\frac{y(x)}{x}$ , $b=\lim_{x \to \infty}(y(x)-x)$

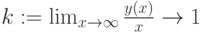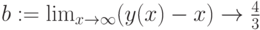
$k:=\lim_{x \to \infty}\frac{y(x)}{x}\to 1$ , $b:=\lim_{x \to \infty}(y(x)-x)\to \frac{4}{3}$

Ассимптота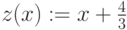 $z(x):=x+\frac{4}{3}$

Предел производной в точке x=0 слева и справа:

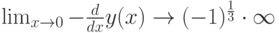
$\lim_{x \to 0}-\frac{d}{dx}y(x)\to (-1)^{\frac{1}{3}}\cdot \infty$

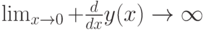
$\lim_{x \to 0}+\frac{d}{dx}y(x)\to \infty$

В нуле функция непрерывна, но производная имеет разрыв второго порядка.

Матричные операции

При моделировании экономических задач данные часто имеют табличный вид, математическая модель представляет систему уравнений. Для решения таких задач удобно представлять данные в виде матриц и решать задачу в матричном виде. В Mathcad возможны чисто матричные операции: сложения, вычитания и умножения матриц, взятие обратной матрицы, транспонирование матрицы. вычисление определителя квадратной матрицы и т.д. Для этого используется панель Матрица. В первой части были описаны правила работы с матрицами в Mathcad. Дополнительно рассмотрим применение ряда операций для действия над матрицами.

Существует удобная операция векторизации, которая позволяет производить поэлементные вычисления над матрицами, вводится кнопкой палитры Matrix или комбинацией клавиш Ctrl - . При её использовании операции производятся над каждым элементом вектора независимо, так например: f(M) . Стрелка сверху над функцией указывает, что функцию надо вычислять для всех элементов матрицы . Пример векторизации приведен ниже:

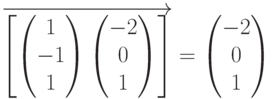
$\overrightarrow{\begin{bmatrix}\begin{pmatrix} 1 \\ -1 \\1 \end{pmatrix}\begin{pmatrix} -2 \\ 0 \\1 \end{pmatrix}\end{bmatrix}}=\begin{pmatrix} -2 \\ 0 \\1 \end{pmatrix}$

В MathCAD имеются встроенные функции для сортировки элементов массива в порядке возрастания или убывания:

– сортировка элементов вектора в порядке возрастания;
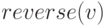– перестановка элементов вектора в обратном порядке;
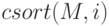– перестановка строк матрицы в порядке возрастания элементов i–го столбца;
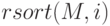– перестановка столбцов матрицы в порядке возрастания элементов –й строки.

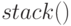Для изменения структуры матриц существует две функции (пример использования функций augment() и stack() ниже).

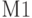объединяет в одну матрицы и , имеющие одинаковое число строк.
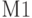объединяет в одну матрицы и , имеющие одинаковое число столбцов.

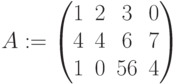
$A:=\begin{pmatrix} 1 & 2 & 3 & 0 \\ 4 & 4 & 6 & 7 \\ 1 & 0 & 56& 4\end{pmatrix}$

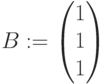
$B:=\begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix}$

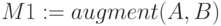
M1:=augment(A,B)

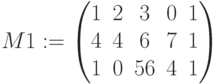
$M1:=\begin{pmatrix} 1 & 2 & 3 & 0 &1 \\ 4 & 4 & 6 & 7 & 1 \\ 1 & 0 & 56& 4 &1\end{pmatrix}$

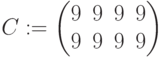
$C:=\begin{pmatrix} 9 & 9 & 9 & 9 \\ 9 & 9 & 9 & 9 \end{pmatrix}$

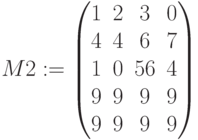
$M2:=\begin{pmatrix} 1 & 2 & 3 & 0 \\ 4 & 4 & 6 & 7 \\ 1 & 0 & 56& 4 \\ 9 & 9 & 9 & 9 \\ 9 & 9 & 9 & 9\end{pmatrix}$

Основные итоги

Приведены этапы экономико-математического моделирования. Описаны математические операции, необходимые при решении математических моделей, реализуемые техникой символьных вычислений в Mathcad. Приведены примеры: решения уравнений, разложения функции в ряд, интегрирования и дифференцирования, исследования функций.

Ключевые термины

Математическая модель – математический образ исследуемой системы, описывающий ее в абстрактной форме и адекватно отражающий структуру, свойства и взаимосвязи.

Системный анализ - метод моделирования, представляющий собой последовательность действий по установлению структурных связей между переменными или элементами исследуемой системы.

Системный синтез - процесс создания моделируемой системы на основе структурных свойств, связей при реализации разработанных требований и целей.

Экономико-математическая модель - математическая модель, предназначенная для исследования экономической проблемы.

Экономико-математическое моделирование - описание экономических процессов и явлений в виде экономико-математических моделей.

Mathcad - популярный математический пакет из класса систем автоматизированного проектирования, ориентированный на подготовку интерактивных документов с вычислениями и визуальным сопровождением, используется для обучения, решения математических, инженерно-технических и научных задач.

Дифференцирование - операция нахождения производной функции, характеризующей скорость ее изменения в данной точке.

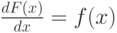Интегрирование - нахождение первообразной F(x) для данной функции f(x) , такой что, $\frac{dF(x)}{dx}=f(x)$ . Обозначение: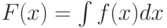 $F(x)=\int f(x)dx$

Уравнение – равенство, содержащее одну или несколько переменных.

Ряд Тейлора - степенной ряд, описывающий поведение данной функции f( х) в окрестности заданной точки.

Функция - соответствие между переменными величинами х и у, в результате которого каждому значению величины (независимой переменной, аргументу) сопоставляется одно-единственное значение величины (зависимой переменной).

Матрица - прямоугольная таблица каких- либо элементов (чисел, математических выражений), состоящая из строк и столбцов.

Дальше >>

Сервисы MATHCAD 14: реализация технологий экономико-математического моделирования

Сервисы MATHCAD 14: реализация технологий экономико-математического моделирования