Языки реляционных баз данных

7.6 Реляционное исчисление на доменах

В реляционном исчислении на доменах (Domain Relational Calculus — DRC) область определения переменных не кортежи отношения, а набор доменов.

Отношение состоит из кортежей, в которые входят значения, принадлежащие доменам. Поэтому необходимо как-то показывать, что некоторые значения на доменах входят в один кортеж. С этой целью в исчисление на доменах, в отличие от исчисления на кортежах, вводится дополнительный набор предикатов, выражающих условия принадлежности (доменов кортежу).

Пусть —это -арное отношение с атрибутами 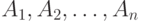. Тогда условие принадлежности можно записать так: 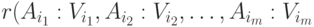, где 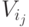- это либо константа, либо имя доменной переменной.

Условие принадлежности истинно тогда и только тогда, когда в отношении г существует кортеж, содержащий заданные значения 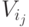указанных -тых атрибутов кортежа , то есть .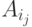

Если 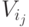— константа, то условие на атрибут. зависит от текущих значений доменных переменных; если же 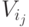— имя доменной переменной, то условие принадлежности может принимать разные значения истинности при разных значениях этой переменной.

Во всех остальных отношениях правильно построенные формулы и выражения исчисления доменов и исчисления кортежей аналогичны. В частности, формулы могут включать кванторы. Различаются свободные и связанные вхождения доменных переменных.

Сравните форму записи запроса в исчислении на доменах 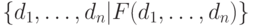и аналогичную форму для исчисления на кортежах .

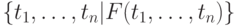7.6.1 Синтаксис запросов DRC в WinRDBI

Запрос имеет вид: 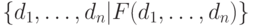, где — формула исчисления, а 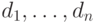— доменные переменные, действующие как глобальные переменные в и определяющие схему результата.

Результатом запроса DRC будет множество всех образованных кортежей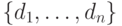, для которых формула истинна.

Обозначим: — переменная-домен, — константа уровня домена, 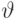— оператор сравнения. Тогда атомами будут: .

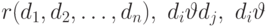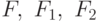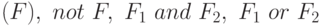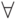Пусть — формулы. Тогда формулами будут: . Если свободна (свободная переменная не квантифицирована действием или ) в 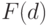, формулами будут , .

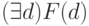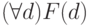7.6.2 Реляционная полнота реляционного исчисления на доменах

Как в исчислении на кортежах, для доказательства достаточно выразить операции реляционной алгебры через операции исчисления. Обозначим условия принадлежности через 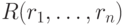. Сведем представления в таблицу 7.3.

Таблица 7.3. Сравнение реляционной алгебры и исчисления на доменах

Реляционная алгебра	Реляционное исчисление на доменах

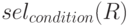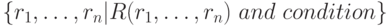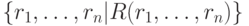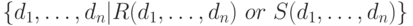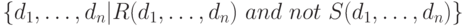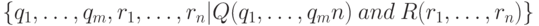7.6.3 Примеры запросов в исчислении на доменах

Войдите в WinRDBI, откройте базу empTraining.rdb и файл empTrain-ing.drc с набором запросов в исчислении на доменах. Форма записи запроса в исчислении на доменах

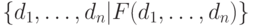
похожа на аналогичную форму для исчисления на кортежах

,

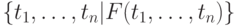но формула исчисления на доменах обязательно содержит условие приадлежности домена кортежу. Пример запроса:

qSelection :=
{ EID, ELast, EFirst, ETitle, ESalary | employee(EID, ELast, EFirst, ETitle, ESalary) and ESalary > 100000 };

Переменные EID, ELast, EFirst, ETitle, ESalary доменные, а employee(EID, ELast, EFirst, ETitle, ESalary) — условие связи.

В следующем запросе takenCourse :={ EID | akes(EID, _, _, _, _)}; перед вертикальной чертой упомянута только одна доменная переменная. Поэтому в условии соединения знаками подчеркивания пришлось отметить остальные "безразличные" переменные. Запрос "Какие курсы предлагаются в области баз данных?", в котором предлагается вывести атрибуты cID, cTitle, cHours, дает пример соединения (рисунок 7.4

Рис. 7.4. Соединение отношений technologyArea и trainingCourse

Сравните его с эквивалентным запросом в исчислении на кортежах (рисунок 7.3)

7.7 Запросы, основанные на реляционной алгебре и на исчислениях

Результат выполнения любой операции алгебры — это элемент базисного множества. В случае реляционной алгебры - отношение. Ранее было показано, что соединение двух отношений выполняется через декартово произведение, то есть сначала выполняется декартово произведение, а потом на нем выполняется операция селекции. На практике, если таблицы большие, то результата такого запроса придется ждать очень долго. Поэтому от реализации реляционной алгебры отказались очень давно.

Основное отличие языков, основанных на реляционной алгебре и на исчислениях, состоит в уровне процедурности. Запросы, основанные на реляционной алгебре, задают дерево алгебраических операций, то есть имеют однозначную процедурную интерпретацию (с учетом старшинства операций и расстановки скобок). Запрос реляционного исчисления не имеет однозначной процедурной интерпретации. Он только устанавливает условия, которым должны удовлетворять кортежи результирующего отношения. Поэтому языки реляционного исчисления являются менее процедурными и, соответственно, более декларативными.

Любой реляционно-полный язык позволяет не только моделировать язык запросов реляционной алгебры, но и языки запросов реляционных исчислений на кортежах или на доменах. То есть языки исчислений могут быть шире, но минимальный уровень моделируется реляционно-полным языком.