Языки реляционных баз данных

7.2 Понятие исчисления. Свойства исчислений

В соответствии с общими понятиями семиотики будем выделять синтаксис (способ записи чего-либо), семантику (смыслы) и прагматику (способы употребления). Эта трехчастная конструкция называется треугольником Фреге. Заметим, что насыщение баз данных смыслами мало изучено, но может представлять большой интерес как для практики, так и для обучения.

Займемся исчислениями. Изложение по недостатку места и времени будет неполным и поверхностным, но достаточным для практического освоения исчислений на кортежах и доменах.

7.2.1 Логические исчисления

Определение. Исчисление — это "дедуктивная система, т.е. способ задания множества путем указания исходных элементов (аксиом исчисления) и правил вывода, каждое из которых описывает, как строить новые элементы из исходных и уже построенных. Выводом в исчислении G называется такое линейно упорядоченное множество, что всякий его элемент Р является либо аксиомой исчисления G, либо заключением применения какого-либо принадлежащего О правила вывода, причем все посылки этого применения предшествуют Р в выводе".

Дедуктивной называют систему, в которой работает дедуктивный вывод.

Исчисление высказываний изучает логические связи между высказываниями, рассматриваемыми как единое целое, без учета их строения. Значений истинности два. Третье значение истинности "полуистинно-полуложно" (или значение "не знаю"), связанное с NULL, здесь не используется.

Исчисление предикатов формализует логику, изучающую субъектно-предикатную структуру высказываний. Предполагается, что в высказывании есть некоторые переменные, и потому истинность предиката может быть разной в зависимости от того, как вы означите эти переменные.

7.2.2 Алгебра множеств и логика

Когда вы будете пытаться понять разницу в эффективности языков, основанных на исчислениях и на реляционной алгебре, обратите внимание на то, что в школьной математике принято допускать одну неточность. Операции над множествами и логические операции там часто иллюстрируют на примере линейно упорядоченных множеств. То есть работают с интервальными, а не произвольными множествами. Потому операции над множествами и эквивалентные операции над соответствующими предикатами, по сути, совпадают, точнее, находятся во взаимно-однозначном соответствии.

Отношения — это неупорядоченные множества кортежей, и потому вычисление предикатов может быть существенно эффективнее действий над множествами кортежей. В алгебре результат каждой операции — это промежуточное отношение, которое в реализациях языка должно быть создано. При этом работают со всеми кортежами, а не только с граничными элементами, как в интервальных множествах. В простых запросах в исчислениях могут проверяться сложные условия, выраженные предикатами, и строиться единственное результирующее отношение.

7.2.3 Предикаты

Исчисление высказываний не позволяет оперировать обобщенными утверждениями, содержащими переменные. Этот недостаток устраняется использованием предикатов.

Определение. Предикат 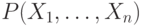—это утверждение 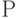об объектах .

Сами объекты могут рассматриваться как переменные, означивая которые мы получаем из предиката высказывания с разными значениями истинности. Можно понимать предикат как функцию в множество значений истинности . Примеры:

1. Высказывание: погода (вторник, дождь).
2. Предикат: погода .

Здесь "погода" — предикатный символ (предикат); и — переменные; "вторник", "дождь" — константы.

Одноместные предикаты обозначают свойства (например, "быть человеком"), предикаты двухместные и с большей арностью обозначают отношения и операции. Пример: двухместный предикат "выше, чем".

Особый интерес представляют предикаты, значение истинности которых определяется на некотором наборе переменных. Высказывания о множествах объектов строятся с помощью кванторов.

Кванторы

Широко используются:

1. квантор всеобщности 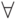— "для всех".
2. квантор существования — "существует".

Реже употребляется: сильный квантор существования 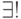- "существует единственный". Примеры:

Переменная, на которую навешен квантор, называется связанной. Например, в формулах 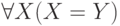и переменная связана, а свободна.

7.2.4 Понятие исчисления

Важно понимать, что исчисление или формальная теория —это система правил оперирования со знаками, используемая для доказательства или опровержения предложений, выразимых с помощью допустимого набора знаков. Исчисления работают с так называемыми правильно построенными формулами (ППФ). Аксиомы — это набор ППФ, принятых за исходные. В самом исчислении нет представления об истинности аксиом.

Кроме знаков ничего нет — никаких смыслов. Но исчисление может быть интерпретировано. И вот тогда появляется семантика.

Исчисление состоит из:

• набора символов, образующих алфавит (символ —не обязательно буква, например, слово);
• набора правильно построенных формул — ППФ (well-formed formulas — WFF);
• выделенного подмножества правильно построенных формул, называемых аксиомами;
• правил вывода, определяющих способ получения формул из других формул.

Выделяют логические аксиомы, определяющие базовую логику. Специфика теории может потребовать добавления нелогических аксиом.

Мы будем рассматривать исчисления с конечным алфавитом, конечным числом аксиом и формулами конечной длины.

Правила вывода

Используются, в частности, следующие правила вывода:

• modus ponens (правило отделения): Если и — истинны, то выводимо .
• modus tollens: Если истинно и — ложно, то выводимо —.

Формальное доказательство формулы в исчислении — это построение конечной последовательности формул 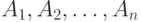, причем, 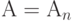. Каждая из формул этой цепочки либо аксиома, либо получена из других формул с помощью правил вывода. называется теоремой. С помощью символа "доказуемо" 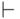запишем этот факт как .

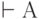Свойства исчисления

Определяющими свойствами любого исчисления являются полнота и непротиворечивость.

Определение (Полнота). Формальная теория называется полной, если для любого высказывания А логики предикатов или или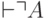

Определение (Непротиворечивость). Формальная теория называется непротиворечивой, если формула 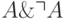в ней недоказуема для произвольного высказывания А теории.

Замечание. Как показал К. Гедель в своей знаменитой теореме о неполноте арифметической логики, доказательство непротиворечивости невозможно выполнить даже в рамках формальных теорий для простых математических объектов.

7.2.5 Языки запросов, основанные на логических исчислениях

Реляционная алгебра определяет набор операций, комбинируя которые, можно создать отношение, которое представляет ответ на запрос.

Существует еще три в некотором смысле эквивалентных подхода к построению систем запросов - реляционные исчисления на кортежах, на доменах и, так называемые, табло.

Знания только реляционной алгебры даже для практики недостаточно, потому что два наиболее известных языка для работы с реляционными базами данных — SQL (Structured Query Language) и QBE (Query-by-Example) — основаны, соответственно, на реляционных исчислениях на кортежах и доменах.

В настоящее время языками, основанными на реляционной алгебре, не пользуются. Так зачем же мы ее изучаем? По двум причинам:

• язык реляционной алгебры служит своеобразным эталоном для языков запросов к реляционной базе данных;
• вторая причина в том, что современные языки, предназначенные для работы с базами данных, не удается сделать достаточно мощными, используя единственную математическую модель; так, в SQL реляционной модели данных соответствуют только очень простые запросы.

Определение. Язык запросов к базе данных, способный моделировать реляционную алгебру, обладает свойством реляционной полноты. Используемые в практике языки сверхполны, то есть кроме реляционных запросов, они позволяют делать много чего еще. Понятно, что реляционно-неполные языки интереса не представляют.

Удобство исчислений в том, что в запросах формируются условия, которым должен удовлетворять результат запроса. По ним и отбираются строки. В запросах реляционной алгебры при выполнении каждой операции последовательно получаются промежуточные отношения. Это замедляет получение ответа.