| Россия |
Языки реляционных баз данных
7.5 Реляционное исчисление предикатов на кортежах
В реляционном исчислении на кортежах (Tuple Relation Calculus — TRC) правильные формулы строятся как описания условий, которым должны удовлетворять кортежи, образующие искомые отношения. Эти условия в простейшем варианте имеют вид:  . Здесь
. Здесь  — переменная, обозначающая некоторый кортеж, а
— переменная, обозначающая некоторый кортеж, а 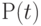 —предикат. Формула исчисления кортежей описывает множество всех таких кортежей, для которых предикат принимает значение "истина". Общий вид правильно построенных формул исчисления на кортежах приведен в разделе 7.5.5.
—предикат. Формула исчисления кортежей описывает множество всех таких кортежей, для которых предикат принимает значение "истина". Общий вид правильно построенных формул исчисления на кортежах приведен в разделе 7.5.5.
7.5.1 Состав предиката Р(i) в исчислении на кортежах
Элементарными образующими предиката  являются атомы трех видов — переменные кортежи, отношения между кортежами и отношения между кортежем и константой. Опишем их:
являются атомы трех видов — переменные кортежи, отношения между кортежами и отношения между кортежем и константой. Опишем их:
- Переменные кортежи:
 , где
, где  — отношение. Данный атом имеет значение "истина", если кортеж
— отношение. Данный атом имеет значение "истина", если кортеж  принадлежит отношению
принадлежит отношению  . При этом если отношение имеет схему
. При этом если отношение имеет схему  , то и кортеж
, то и кортеж  имеет такую же схему.
имеет такую же схему. - Специфика реляционного исчисления на кортежах в том, что элементы рассматриваемого множества — это кортежи, которые обязательно принадлежат некоторым отношениям. И переменные в нем — это переменные кортежи.
- Пример: Пусть отношение СОТРУДНИК имеет схему {ИМЯ, ФАМИЛИЯ, ОТЧЕСТВО, ВОЗРАСТ}. Утверждение
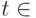 СОТРУДНИК, означает, что
СОТРУДНИК, означает, что  является кортежем отношения СОТРУДНИК, и имеет ту же схему: {ИМЯ, ФАМИЛИЯ, ОТЧЕСТВО, ВОЗРАСТ}.
является кортежем отношения СОТРУДНИК, и имеет ту же схему: {ИМЯ, ФАМИЛИЯ, ОТЧЕСТВО, ВОЗРАСТ}. - Отношения между кортежами (записываются в точечном синтаксисе):
 , где
, где  и
и  — некоторые кортежи,
— некоторые кортежи,  и
и  — имена атрибутов,
— имена атрибутов,  и
и  — множества атрибутов, причем
— множества атрибутов, причем 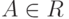 и
и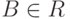 , а
, а  — оператор сравнения. Этот атом принимает значение "истина", тогда и только тогда, когда атрибут
— оператор сравнения. Этот атом принимает значение "истина", тогда и только тогда, когда атрибут  кортежа
кортежа  находится в отношении
находится в отношении  с атрибутом
с атрибутом  кортежа 1 Например, если
кортежа 1 Например, если 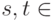 СОТРУДНИК, то
СОТРУДНИК, то  .ВОЗРАСТ <
.ВОЗРАСТ <  .ВОЗРАСТ истинно, если возраст сотрудника s меньше возраста сотрудника .
.ВОЗРАСТ истинно, если возраст сотрудника s меньше возраста сотрудника . - Отношения между кортежем и константой:
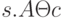 , где
, где  — некоторый кортеж,
— некоторый кортеж,  — имя атрибута (
— имя атрибута ( 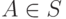 ), а
), а  — константа из домена атрибута
— константа из домена атрибута  . Атом принимает значение "истина", если значение атрибута кортежа находится в отношении
. Атом принимает значение "истина", если значение атрибута кортежа находится в отношении  с константой
с константой  . Например,
. Например,  .ВОЗРАСТ < 40 истинно, если возраст сотрудника
.ВОЗРАСТ < 40 истинно, если возраст сотрудника  меньше 40.
меньше 40.
7.5.2 Правильно построенные формулы исчисления на кортежах
Могут использоваться логические операции, кванторы и скобки. Рекурсивное определение правильно построенных формул:
- Атом — это ППФ.
- Если
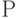 и
и  — ППФ, то
— ППФ, то 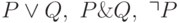 будут ППФ.
будут ППФ. - Если
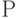 — ППФ, то
— ППФ, то 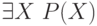 — ППФ.
— ППФ. - Если
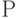 — ППФ, то
— ППФ, то  — ППФ.
— ППФ. - Если
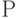 — ППФ, то
— ППФ, то  - ППФ.
- ППФ. - Ничто иное не является ППФ.
Замечание. Квантор существования в инструментальном средстве WinRDBI обозначается как EXISTS, квантор всеобщности как FORALL.
7.5.3 Сопоставление операторов реляционной алгебры и формул исчисления на кортежах
- Объединение:

- Разность:

- Селекция:
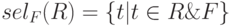
Здесь  и
и  — отношения,
— отношения,  — формула.
— формула.
7.5.4 О реляционной полноте языка запросов
Как определено ранее, язык запросов к реляционной базе данных называется реляционно-полным, если он, по крайней мере, так же выразителен, как язык запросов реляционной алгебры. Иначе говоря, реляционно-полный язык позволяет, по крайней мере, моделировать язык запросов реляционной алгебры. Используемые в практике языки запросов "более чем полны" за счет:
- включения арифметики и вычисления однострочных функций;
- включения агрегатных (многострочных) функций;
- иногда за счет вычисления транзитивного замыкания отношения.
7.5.5 Синтаксис запросов TRC в WinRDBI
Запрос (ППФ) имеет вид: 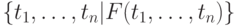 , где
, где  — формула исчисления, а
— формула исчисления, а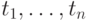 — кортежные переменные, действующие как глобальные переменные в
— кортежные переменные, действующие как глобальные переменные в  и определяющие схему результата.
и определяющие схему результата.
Обозначим  и
и 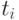 — переменные кортежи,
— переменные кортежи, 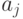 — атрибут,
— атрибут,  — константа уровня домена,
— константа уровня домена, 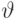 — оператор сравнения. Тогда атомами будут:
— оператор сравнения. Тогда атомами будут: 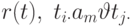 . Пусть
. Пусть 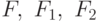 — формулы. Тогда формулами будут:
— формулы. Тогда формулами будут:  and
and 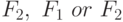 . Если
. Если  свободна (переменная свободна в формуле, если она не квантифицирована действием exists или forall) в
свободна (переменная свободна в формуле, если она не квантифицирована действием exists или forall) в 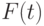 , то формулами будут
, то формулами будут 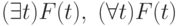 .
.
7.5.6 Реляционная полнота реляционного исчисления на кортежах
Как вы помните, для доказательства достаточно выразить операции реляционной алгебры через операции исследуемого исчисления. Сведем представления операций реляционной алгебры формулами реляционного исчисления на кортежах в таблицу 7.2.
Исчисление первого порядка на кортежах реляционно полно, так как мы смогли операции реляционной алгебры представить в виде операций реляционного исчисления на кортежах.
| Реляционная алгебра | Реляционное исчисление на кортежах |
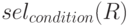 |
 |
 |
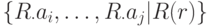 |
 |
 |
 |
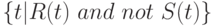 |
 |
 |
Рассмотрим несколько примеров.
7.5.7 Примеры запросов в исчислении на кортежах
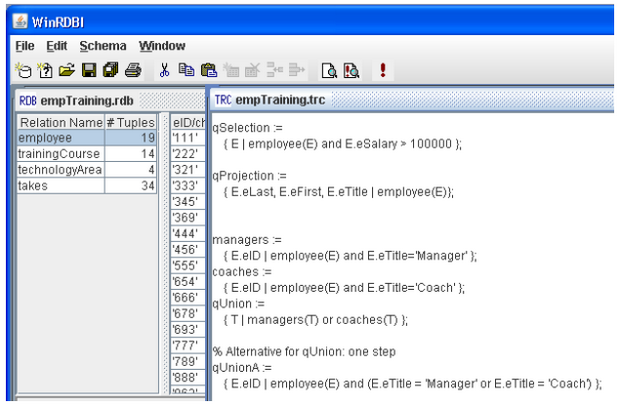
Войдите в WinRDBI, откройте базу empTraining.rdb и файл empTrain-ing.trc с набором запросов в исчислении на кортежах (рисунок 7.1).
Все запросы имеют единую структуру вида {ti,... ,tn\F (ti,...,tn)}. Разберитесь с десятком примеров, особенно сложных, помещенных в конце списка в правом окне.
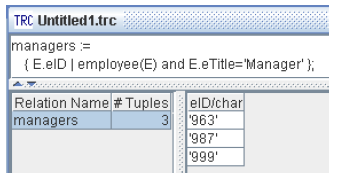
Обратите внимание на создание новых отношений (рисунок 7.2), и соединения отношений, например, в запросе "Какие курсы предлагаются в области баз данных?" (рисунок 7.3).
Как вы помните, (exists A) это квантор существования.