| Россия |
Реляционная модель данных
4.2 Операции проекции и соединения. Декомпозиция отношений.
Изучим две операции над отношениями — проекцию и естественное соединение. Это позволит рассмотреть разбиение (декомпозицию) отношения на его проекции и восстановление исходного отношения путём соединения этих проекций. Обнаружатся неожиданные для начинающих неполные декомпозиции.
Описания всех остальных операций даны в разделе 4.6.
Определение. Проекция —это набор унарных операций выбора подмножества атрибутов отношений 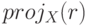 projx(r), где
projx(r), где  — схема отношения
— схема отношения  и
и 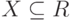 — набор атрибутов.
— набор атрибутов.
Пример проекции отношения с атрибутами  на подмножество
на подмножество 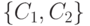 приведён ниже:
приведён ниже:
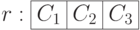
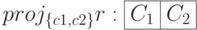
Свойство. Если 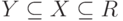 , то
, то 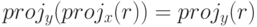 .
.
Определение (Естественное соединение). Пусть отношения 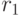 и
и 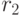 имеют схемы
имеют схемы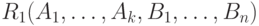 и
и 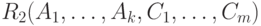 . Тогда естественное соединение отношений
. Тогда естественное соединение отношений 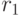 и
и 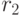 есть отношение
есть отношение 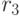 со схемой
со схемой 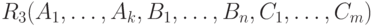 , в котором каждая запись(экземпляр) получена конкатенацией каждой записи из
, в котором каждая запись(экземпляр) получена конкатенацией каждой записи из 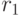 с теми записями из
с теми записями из 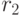 , у которых совпадают значения в общих атрибутах
, у которых совпадают значения в общих атрибутах  .
.
Естественное соединение отношений 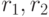 с общим атрибутом
с общим атрибутом  приведено ниже:
приведено ниже:

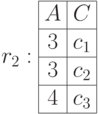 .
.
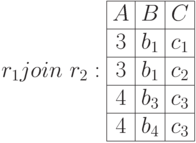
Обозначение естественного соединения: 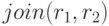 или
или  или
или  .
.
Рассмотрим декомпозицию отношения подробнее.
Определение. Полная декомпозиция отношения — это набор его проекций, соединение которых идентично отношению.
Существуют неполные декомпозиции!
Пример полной декомпозиции приведен ниже.
Декомпозируемое отношение:
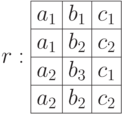
Проекции, дающие полную декомпозицию (вычеркиваем повторяющиеся записи):
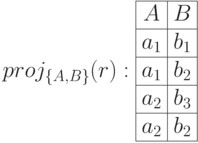
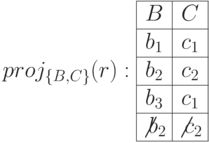
Для исходного отношения 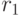 получены проекции на атрибуты
получены проекции на атрибуты 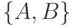 и
и 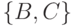 . Соединение их даст исходное отношение. Соедините проекции сами.
. Соединение их даст исходное отношение. Соедините проекции сами.
Для некоторых проекций декомпозиция оказывается неполной. Это означает появление так называемых присоединённых записей, которых не было в исходном отношении.
Соединение проекций 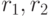 того же отношения
того же отношения  создает присоединенные записи:
создает присоединенные записи:
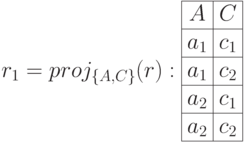
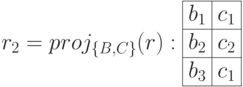
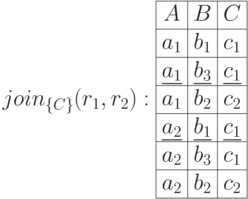
В восстановленном исходном отношении появились выделенные (подчерктутые) две записи, которых в исходном отношении  не было.
не было.
4.3 Первичный ключ. Роль функциональных зависимостей
Уточнение понятия ключа (Первичный ключ отношения). Атрибут или набор атрибутов, значения которых позволяют однозначно выбрать кортеж отношения, называется первичным ключом.
Определение. Ключ, состоящий из одного атрибута, называют простым.
Определение. Ключ, состоящий из двух или более атрибутов, называют составным или конкатенированным.
Определение (Суррогатный ключ). Суррогатным называется ключ, не имеющий прототипа в предметной области. Обычно он генерируется приложением.
Утверждение. Из того, что кортежи отношений не повторяются, следует, что любое отношение имеет ключ.
Заметим, что в ключ могут войти все атрибуты отношения.
Утверждение. Пополнение ключа еще одним (не ключевым) атрибутом есть ключ.
Определение (Минимальный ключ). Если удаление одного атрибута лишает ключевой набор атрибутов статуса ключа, то такой ключ называют минимальным.
Замечание. Первичным ключом называют в действительности минимальный первичный ключ (рисунок 4.4).
Замечание. Изучая базы данных, следует понимать, что все приводимые примеры по необходимости сделаны простыми. Всегда следует ограничиваться контекстом примера и не пытаться рассуждать "как в жизни" или "как может быть". Так в отношении на рисунке 4.4. можно было спросить: "А как быть с теми, у кого нет ИНН?". Так вот, в примере предполагается, что ИНН есть у всех и другие варианты не рассматриваются.
При проектировании реальных баз данных необходимые ориентиры дает спецификация модели бизнеса.
Функциональные зависимости (ФЗ) на отношениях и зависимости связанные с обобщениями функций играют важную роль в теории баз данных. В частности, ключи определяются через функции (рисунок 4.5).
Утверждение. Любой атрибут находится в функциональной зависимости от ключа. Могут существовать и другие функциональные зависимости.