| Россия |
Реляционная модель данных
4.6.2 Декартово произведение
Определение. Декартовым произведением отношений  и
и  арностей
арностей 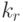 и
и 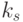 , с непересекающимися множествами атрибутов, соответственно
, с непересекающимися множествами атрибутов, соответственно  и
и  , называется отношение
, называется отношение 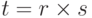 арности
арности 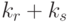 , состоящее из кортежей, первые
, состоящее из кортежей, первые 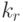 компонентов которых есть кортежи из
компонентов которых есть кортежи из  , а последние
, а последние 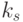 компонентов выбираются из
компонентов выбираются из  . Иначе говоря, кортежи
. Иначе говоря, кортежи  образованы конкатенацией каждого кортежа из
образованы конкатенацией каждого кортежа из  с каждым кортежем из
с каждым кортежем из  . Поэтому, если в текущем состоянии
. Поэтому, если в текущем состоянии  и
и  имеют
имеют 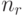 и
и  кортежей, то в
кортежей, то в  их
их  .
.
Замечание. В одном отношении недопустим повтор имен. Поэтому, в частности, не существует декартов квадрат. При соединении отношений с одноименными атрибутами некоторые из них могут быть переименованы исходя из семантики данных и соединения.
Рассмотрим пример декартова произведения:
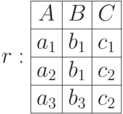
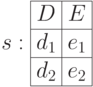
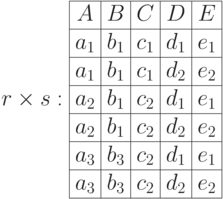
4.6.3 Селекция (выбор)
Определение. Пусть  — формула, образованная:
— формула, образованная:
- операндами в виде констант и имен столбцов (номеров столбцов);
- операторами сравнения
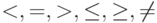 ;
; - логическими операторами
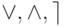 (дизъюнкция, конъюнкция, отрицание).
(дизъюнкция, конъюнкция, отрицание).
Тогда результат селекции 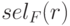 selp(r) есть множество кортежей
selp(r) есть множество кортежей  из
из  , для которых формула
, для которых формула  истинна.
истинна.
Рассмотрим пример селекции по условию  :
:
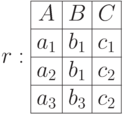
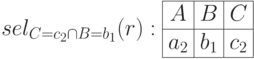
4.6.4 Булевы операции
Два отношения 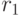 и
и 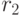 с одной и той же схемой
с одной и той же схемой  могут рассматриваться как подмножества множества всех возможных кортежей в схеме
могут рассматриваться как подмножества множества всех возможных кортежей в схеме  . Поэтому к ним применимы булевы операции пересечения, объединения и разности
. Поэтому к ним применимы булевы операции пересечения, объединения и разности 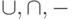 .
.
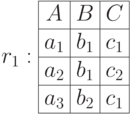
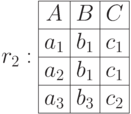
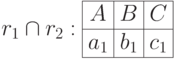
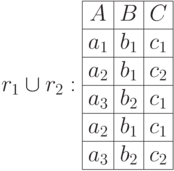
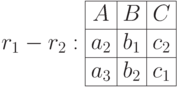
Естественно, отношения с разными схемами несовместимы. Однако, операция переименования атрибутов, которую мы рассмотрим позже, в отдельных случаях может сделать разносортные отношения совместимыми.
4.6.5 Дополнение
В определении дополнения возникают трудности. Пусть 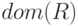 есть множество всех возможных кортежей над атрибутами схемы
есть множество всех возможных кортежей над атрибутами схемы  с определенным для каждого атрибута доменом.
с определенным для каждого атрибута доменом.
Если хотя бы один домен бесконечен, то полное отношение 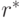 , включающее все элементы из
, включающее все элементы из 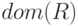 , не будет отношением в понимании реляционной алгебры.
, не будет отношением в понимании реляционной алгебры.
Не будет отношением и дополнение к конечному отношению  :
:
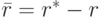
Поэтому реляционную алгебру естественно рассматривать, не включая в неё дополнения.
4.6.6 Частное
Рассмотрим самую странную, на первый взгляд, операцию —частное.
Определение. Пусть даны отношение  с арностью
с арностью 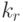 и схемой
и схемой  и отношение
и отношение  с арностью
с арностью 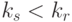 и схемой
и схемой  , такой что
, такой что 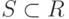 и
и 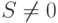 . Тогда частным называется отношение
. Тогда частным называется отношение  арности
арности  , которое содержит столбцы отношения
, которое содержит столбцы отношения  , отсутствующие в
, отсутствующие в  . Часть записи
. Часть записи  включается в
включается в  , если в
, если в  она сцеплена с каждой записью из
она сцеплена с каждой записью из  .
.
Смысл этой операции будет понятен позднее при изучении многозначных функциональных зависимостей (MV-зависимостей).
Обозначение:  или
или  или
или 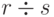
Рассмотрим пример частного:
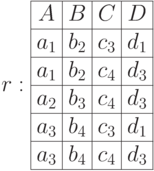
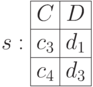
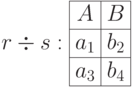
4.7 Совместимость отношений и переименование атрибутов
Переименование атрибутов — самая необычная операция реляционной алгебры. Выясним, зачем она может понадобиться. Уже говорилось, что операции объединение, пересечение и разность, требуют, чтобы отношения-операнды были совместимы, то есть относились к одному сорту. Такие отношения отличаются только именами и состояниями. Сигнатуры у них одинаковы, то есть количество атрибутов одно и то же и атрибуты попарно совпадают по типам, а в простейшем случае, ещё и по именам.
Если же имена отношений и/или атрибутов не совпадают, необходимо установить соответствие между именами или изменить некоторые из имён. Естественно, приводить к одному имени можно только атрибуты, имеющие одинаковый смысл.
Если операнды содержат одинаковые атрибуты, то в операциях соединений и декартовом произведении могут появляться повторяющиеся атрибуты. Это делает невозможным выполнение операции. И здесь переименование может решить проблему. В отличие от приведения к одному имени, тут выполняется разделение имени, которое должно сопровождаться уточнением смыслов образованных имён.
Итак, некоторые несовместимые отношения могут стать совместимыми после переименования атрибутов. Для реализации такой возможности в реляционную алгебру вводится операция переименования атрибутов.
Рассмотрим несколько примеров переименования.
Пример
Необходимо объединить отношения "Employee" и "Работники" для расчета суммарной заработной платы. Схемы отношений:
Employee (empno, ename, salary, mgr) Работники (Тно, ФИО, зарплата, Тно_нач)
где Тно — табельный номер, Тно_нач — табельный номер начальника.
Выполняем переименования атрибутов: Тно — empno, ФИО — ename, зарплата —salary, Тно_нач — mgr. Типы и смысл соответствующих атрибутов считаются одинаковыми.
Один из вариантов команды переименования атрибутов выглядит так: [имя_отношения] RENAME список_старых_атр AS список_новых_атр.
В рассмотренном примере имена объединялись.
Пример
Переименование атрибутов необходимое для объединения отношения с собой.
Скажем, необходимо выбрать всех сотрудников и их непосредственных начальников. Ответ можно получить из декартова произведения только что введённого отношения Employee с собой после переименования. Его схема после переименования атрибутов empno, ename, salary, mgr для начальников в empno_mgr, ename_mgr, salary_mgr, mgr_mgr, соответственно, выглядит так:
(empno, ename, salary, mgr, empno_mgr, ename_mgr, salary_mgr, mgr_mgr).
В этом примере имена разделялись. Смысл атрибутов с суффиксом _mgr тот же, что раньше, но характеризует только сотрудников как начальников.
