| Россия |
Реляционная модель данных
Для того, чтобы изучение реляционной алгебры не превратилось в скучный перечень операций, мы их вводим порциями, достаточными для получения какого-нибудь интересного результата.
Сначала определим операцию декомпозиции — разбиения заполненного отношения на части. Удивительно, но не всегда воссоединение компонент дает исходное отношение. В этом случае декомпозиция называется неполной. На языке алгебры декомпозиция и воссоединение компонент определяются, соответственно, операциями проекции и естественного соединения.
Оказывается, функциональные зависимости, определенные на отношениях, дают естественный язык для задания идентификаторов кортежей отношений (ключей) и для формулирования теоремы Хиса, позволяющей выделить допустимые декомпозиции.
Выделим набор независимых операций. Рассмотрим самую необычную для алгебры операцию переименования атрибутов.
Разберёмся с отображением модели "сущность-связь" в реляционную модель.
В самом конце главы перейдём к реализациям и рассмотрим соотношения между реляционной и табличными моделями.
К 70-м годам направление баз данных представляло мощную индустрию, в которой доминировали иерархические и сетевые модели.
К 1973-му году был принят стандарт CODASYL, определивший общепринятые особенности сетевой модели. Он определил понятия простого и составного элементов данных — аналогов простого поля записи и агрегата. Запись —это именованный агрегат, не входящий ни в какой другой агрегат. В записях можно использовать неопределённое значение. Определялось два типа агрегатов — "вектор", состоящий из простых элементов данных, и "повторяющаяся группа элементов". При этом повторяющаяся группа может образовываться элементами данных, векторами, агрегатами и другими повторяющимися группами.
Наборы представляют связи между типами записей. Как упоминалось в разделе 3.3.1, термин "набор" в модели CODASYL не совпадает с употребляемым нами термином "набор записей". Можно определить любое количество типов наборов между двумя типами записей. Тип набора — это двучленная конструкция, объединяющая тип записи владельца набора и типы записей-членов набора.
В это же время в 1970 г. появилась основополагающая работа Э.Ф.Кодда, в которой он применил к описанию баз данных алгебру отношений — реляционную алгебру. Появилась реляционная модель данных, представляющая базу данных как набор отношений, может быть связанных. Началась эра реляционных баз данных.
Можно спросить, чего же не хватало в существовавших моделях данных? Что обеспечило победное шествие реляционной модели, которому не помешало низкое быстродействие первых её реализаций? Иерархической и сетевой модели не хватало математической убедительности, то есть отсутствовала простая и красивая математическая модель. Это бы ещё полбеды. Плохо то, что в старых моделях было много обременительно лишнего. Язык манипулирования данными и язык запросов носили навигационный характер и требовали знания деталей структуры базы.
Принятие реляционной модели широким кругом пользователей и вендоров обеспечило развитие математической теории, и создание стандартов для её реализаций. Вот с реализациями получилась весьма интересная история. С некоторой стадии их развития математические идеи иссякли и теперь развитие языков манипулирования данными и запросов направляют другие движущие силы. Но об этом мы поговорим в главах, начиная с 8-й. Изменения вызванные практическими потребностями, настолько велики, что в настоящее время реляционные модели практически заменены тем, что в дальнейшее мы будем называть табличными моделями или моделями реляционного типа. Поэтому, кроме отношений в конце этой главы будем рассматривать таблицы.
Давайте разберёмся с основами реляционной модели данных.
4.1 Отношения и их свойства. Схема и состояния отношения
Основные структуры данных в реляционной модели — отношения и атрибуты.
Схему отношения можно определить через задание предиката. Спецификациям отношений соответствуют предикаты. При этом типу записи соответствует предикатный символ, а полям соответствуют аргументные места предикатного символа.
Пример предиката, соответствующего спецификации отдела приведен на рисунке 4.1.
Каждой записи соответствует высказывание (на языке Пролог — факт), например, отдел(001, "Рога и копыта", "Нью-Москва")?
Принадлежность кортежа к отношению определяется истинностью описывающего его предиката.
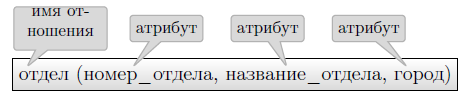
Однако, в реляционной модели принято говорить об отношениях, которые имеют имя и набор свойств, называемых атрибутами (рисунок 4.2).
Под сигнатурой отношения будем понимать набор, состоящий из имени отношения, имён и типов его атрибутов. Отношения без атрибутов не рассматриваются.
Свойство. Данные в реляционной модели хранятся только в отношениях с конечных числом атрибутов. Других источников данных не существует.
Будем рассматривать отношения как наборы однотипных строк-кортежей. Пример: Отношение "Студент" с атрибутами "Фамилия", "Имя", "Отчество", "Дата_рождения", "Студенческая_группа", "Телефон".
Схема отношения:
Студент(Фамилия, Имя, Отчество, Дата_рождения, Студенческая_груп-па, Телефон)
Каждый студент представляется строкой значений своих атрибутов — кортежем, например,
("Иванов", "Петр", "Сидорович", "22.05.82", 32, "111-0000, 222-0000").
Обратите внимание, на то, что последний атрибут это всего лишь строка "111-0000, 222-0000", и нельзя будет определить, есть ли у Иванова телефон 111-0000. С подстроками модель не работает.
Основные свойства отношений:
- кортежи не упорядочены;
- в отношении не может быть двух одинаковых кортежей;
- атрибуты не упорядочены;
- число кортежей в отношении конечно;
- любой атрибут отношения должен содержать данные одного типа (домена);
- все используемые типы данных простые;
- отношение не обладает метрическими свойствами, такими как ширина столбцов, число записей и т.д.
Свойства отношений для удобства запоминания представлены на рисунке 4.3.
Обратите внимание на то, что простота типов данных вовсе не означает, что хранящиеся значения не имеют какой-нибудь структуры. Однако в рамках реляционной модели мы не можем эту структуру воспринять.
Замечание. В реализациях отсутствие упорядоченности может быть не удобным или не реализуемым, а метрические свойства всегда важны, поскольку они определяют быстродействие.
Замечание. Связей между отношениями, которые мы изучали в модели "сущность-связь", в реляционной модели нет. Связи определяются через ключевые атрибуты. В реализациях они задаются ограничениями целостности первичного ключа и внешнего ключа.
Состоянием отношения называется набор входящих в него кортежей.