|
Добрый день!
Скажите, пожалуйста,планируется ли продолжение курсов по нанотехнологиям? Спасибо, Евгений
|
Методы оценки вычислительных характеристик задач предметной области и поддерживающих их аппаратных платформ
Главными источниками погрешностей являются преобразователи десятичного кода в двоичный, денормализаторы в составе арифметических устройств плавающей запятой и шины данных. Все они имеют  -битную разрядную сетку, конечность которой приводит:
-битную разрядную сетку, конечность которой приводит:
- к абсолютной погрешности представления исходных данных формата фиксированной запятой, которая возникает при преобразовании десятичных чисел в двоичный код конечной разрядности
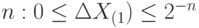 ;
; - к абсолютной погрешности арифметических преобразований, которая включает две составляющие:
-
абсолютную погрешность денормализации, которая характерна для данных формата плавающей запятой:
 , где
, где 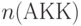 - разрядность регистра-аккумулятора операционного устройства процессора;
- разрядность регистра-аккумулятора операционного устройства процессора; -
абсолютную погрешность округления, которая возникает при пересылке данных из регистра-аккумулятора в регистр общего назначения (РОН) или буферный регистр, для которых
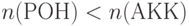 и поэтому
и поэтому 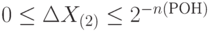 .
.
-
абсолютную погрешность денормализации, которая характерна для данных формата плавающей запятой:
В данном случае объектом исследований являются:
-
Алгоритм сложения с накоплением суммы в однопроцессорной вычис
лительной системе:
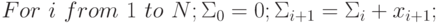
-
2. Алгоритм сложения с накоплением суммы в многопроцессорной вычислительной системе:
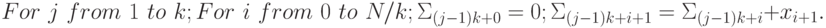
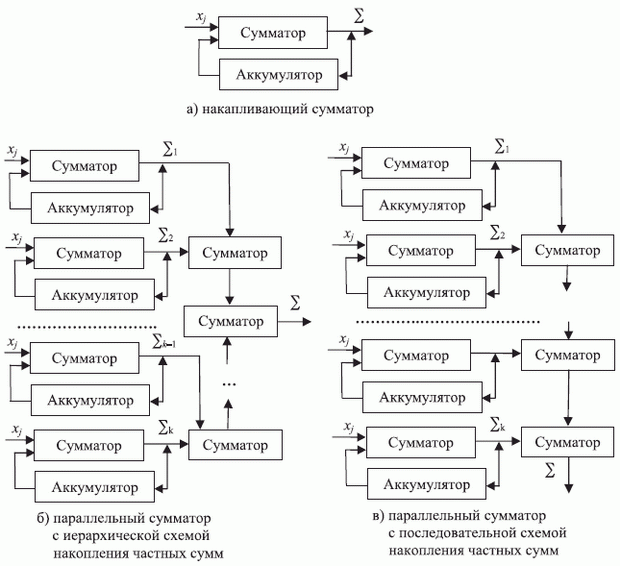
Первому алгоритму отвечает схема суммирования рис. 1.7-а, а второй алгоритм можно реализовать на двух типах аппаратных платформ, которые отличаются количеством операций пересылки частных сумм: с иерархической (рис. 1.7-б) и с последовательной (рис. 1.7-в) схемой накопления частных сумм, где количество сумматоров одинаково и равно 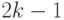 , а время задержки разное и равно соответственно
, а время задержки разное и равно соответственно ![]log_{2} k[+1](/sites/default/files/tex_cache/e71e97f988aaa3fc47c672148a257bd1.png) и
и  (
( ![]log_{2} k [](/sites/default/files/tex_cache/6ec9c108ff6c9ce882d606f4da32237d.png) - старшее целое
- старшее целое  ).
).
Методика управления интенсивностью проявления источников погрешности при вычислении суммы членов псевдослучайной последовательности использует следующие факторы:
- Абсолютная погрешность денормализации зависит от разности порядков слагаемых, которая определяется как накопленной суммой, так и дисперсией псевдослучайной последовательности. Величина накопленной суммы на
 -м шаге зависит от степени упорядоченности псевдослучайной последовательности
-м шаге зависит от степени упорядоченности псевдослучайной последовательности 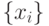 : хронологический порядок перечисления индексов
: хронологический порядок перечисления индексов  , перечисление индексов
, перечисление индексов  по возрастанию
по возрастанию  , перечисление индексов
, перечисление индексов  по убыванию
по убыванию  .
. - Абсолютная погрешность округления зависит от числа внутренних и/или внешних пересылок промежуточных значений накопленной суммы, и она тем выше, чем больше коэффициент распараллеливания вычислений. В схеме рис. 1.7-а всего одна пересылка результата, в схемах рисунков 1.7-б и 1.7-в количество пересылок, в том числе и промежуточных сумм, определяется количеством сумматоров и равно
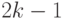 .
.
Чтобы по этой методике исследовать погрешность вычисления суммы членов псевдослучайной последовательности из  элементов в зависимости от различной интенсивности проявления источников погрешностей, достаточно:
элементов в зависимости от различной интенсивности проявления источников погрешностей, достаточно:
- С помощью датчика псевдослучайных чисел построить последовательность чисел
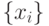 мощности
мощности  .
. - Упорядочить по возрастанию последовательность
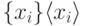 .
. - Упорядочить по убыванию последовательность
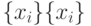 ..
.. - Вычислить
 в однопроцессорном варианте для последовательностей
в однопроцессорном варианте для последовательностей 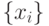 ,
, 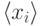 и
и 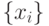 и в двух форматах:
и в двух форматах:  и
и  .
. - Варьируя
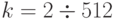 , вычислить суммы в многопроцессорном варианте в формате
, вычислить суммы в многопроцессорном варианте в формате 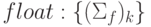 и построить зависимость
и построить зависимость 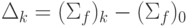 .
.
Из шести возможных вариантов шага 4 наиболее истинное значение 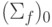 накопленной суммы дает упорядоченная по возрастанию последова-тельность, полученная в формате
накопленной суммы дает упорядоченная по возрастанию последова-тельность, полученная в формате  , то есть
, то есть 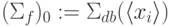 , так как в этом случае оба вычислительных источника имеют минимальную интенсивность.
, так как в этом случае оба вычислительных источника имеют минимальную интенсивность.
Чтобы симулировать погрешность представления, шаг 1 необходимо выполнить сначала в формате  , а затем перейти к формату
, а затем перейти к формату 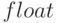 .
.
Типовой график зависимости абсолютной погрешности накопления суммы имеет вид случайного апериодического колебательного процесса (рис. 1.8), который говорит о следующем:
- Колебательный характер обусловлен тем обстоятельством, что накопленные частные суммы могут принимать вид
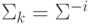 с "единичны-ми" значениями в старших разрядах (например: 0,5, 0,25, 0,75 и т. д.), на которые не влияет ни денормализация, ни округление.
с "единичны-ми" значениями в старших разрядах (например: 0,5, 0,25, 0,75 и т. д.), на которые не влияет ни денормализация, ни округление. - Случайный апериодический характер изменения абсолютной погрешности наиболее опасен потерей управления ходом вычислительного процесса с использованием операторов условных переходов. Поэтому при испытаниях и исследованиях вычислительной устойчивости (Б)ВС имеет смысл варьировать интенсивностью источников погрешностей при вычислении выражений, входящих в операторы
 .
.
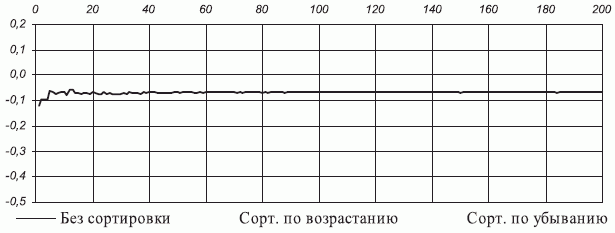
Рис. 1.8. Типовой график зависимости абсолютной погрешности суммирования от коэффициента распараллеливания вычислений, выполненных с одинарной точностью
Таким образом, для создания полноценных синтетических и исследовательских программ нет необходимости усложнять их операционное ядро, которое резко удорожает разработку инструментальных платформ оценки пропускной способности (Б)ВС по потокам инструкций и данных. Для этих целей достаточно в качестве неделимой единицы инструментальной платформы выбрать совокупность представительных задач с прозрачным операционным ядром, позволяющим управлять вычислительной нагрузкой на операционные, коммутационные и управляющие ресурсы ЭВМ и ресурсы ее памяти в соответствии с требованиями всей предметной области.
Системотехнические выводы по лекции 1
- Метрологические проблемы вычислительной техники носят как фундаментальный, так и чисто методический характер. Фундаментальная составляющая связана с отсутствием единой метрики, определяющей количество информации, а значит, и объем выполненной ЭВМ работы. Методическая составляющая связана с отсутствием эталонных ЭВМ, эталонных алгоритмов преобразования данных и стандартных процедур пересчета реальных алгоритмических затрат в затраты эталонного алгоритма. В итоге нарушается базовый принцип любого измерения, в результате чего измерительный прибор становится неотъемлемой частью измеряемого объекта (в данном случае операционной системы) и поэтому постоянно изменяет свою структурно-функциональную схему.
- Согласно результатам третьей лекции курса "Задачи и модели вычислительных наноструктур" проблема создания единой метрики неразрешима в принципе. Действительно, теория вычислений допускает только экстенсиональную эквивалентность двух алгоритмов, то есть эквивалентность по результату, а не в рамках всего вычислительного процесса. С другой стороны, оценку алгоритмической сложности реальных компьютерных реализаций можно провести по А.Н. Колмогорову только с точностью до некоторой константы и при достаточно жестких ограничениях на используемые вычислительные и/или перечислительные алгоритмы, что характерно для алгоритмически ориентированных областей применения традиционных вычислителей.
- Все без исключения инженерные методики оценки производительности фактически отталкиваются от измерения времени, затраченного на решение "хорошо известной пользователю" задачи. В результате сопоставление двух ЭВМ весьма и весьма субъективно, так как и замер времени, и оценка выполненных машиной инструкций, и распределение времени между системными и прикладными задачами носят достаточно субъективный характер.
- Стандартные программные платформы оценки производительности и пропускной способности ЭВМ предоставляют пользователю только возможность создания тестовых программ, которые способны воспроизвести стабильную вычислительную нагрузку реальных задач только при использовании в них циклов
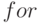 , так как при использовании циклов
, так как при использовании циклов  вычислительная нагрузка зависит от содержимого преобразуемых данных.
вычислительная нагрузка зависит от содержимого преобразуемых данных. - Дальнейшее развитие программных платформ оценки производительности ЭВМ скорее всего будет связано с созданием адаптивных средств, оперативно реагирующих и на специфику алгоритма решения задачи, и на специфику архитектуры ЭВМ, и на содержимое преобразуемых потоков данных.
- Снижение трудозатрат на адаптацию испытательных и исследовательских программ требует структурного подхода, в рамках которого программные модули представительных задач выступают в качестве неделимых единиц. Совокупность таких структурных единиц инструментальной платформы оценки качества ВС должна обеспечить управляемое перераспределение вычислительной нагрузки на операционные, коммутационные и управляющие ресурсы, а также ресурс памяти исследуемой ВС, для чего требуется точная априорная оценка этих же видов ресурсов, затребованных вычислительными алгоритмами представительных задач. Поэтому операционное ядро каждой представительной задачи должно быть алгоритмически прозрачным, чтобы на его основе можно было априорно и достоверно оценить требуемую нагрузку на все виды используемых ресурсов.